数字传输系统的最佳接收与误码性能仿真分析
数字传输系统的最佳接收与误码性能仿真分析
- 1.引言
- 2.系统模型
- 2.1.信道带宽无限时单极性基带传输
- 2.2.信道带宽受限时的双极性基带传输
- 2.3.信道带宽受限时QPSK传输
- 2.4.信道带宽受限时16QAM传输
- 3.仿真过程与仿真结果分析
- 3.1 信道带宽无限时单极性传输系统
- 3.2 信道带宽受限时双极性传输系统
- 3.3 信道带宽受限时QPSK传输系统
- 3.4 信道带宽受限时16QAM传输系统
- 4.小结
1.引言
不同于模拟通信,数字通信是采用的数字信号进行传输,乃是离散信号。是一个个的二进制码,运用编码的方式,把我们所需要传输的消息转化成二进制码,再来传输信号。所用的信道也有两种分别是基带信道和频带信道。两种是分别针对不同情况需求所产用的。实际生活中,大多数传输都是数字频带传输,能够较好的利用信道带宽。
在数字基带传输过程中,确定信号在受到加性高斯白噪声干扰下的最佳接收为采用匹配滤波器,使得在最佳采样时刻的信噪比最大,然后再选择合适的判决门限进行判决,可以使得误比特率最小。在实际数字通信系统中的信道往往是有限的,为此要进一步考虑适合于限带信道传输的限带信号的设计,而在本文中采用的则是广泛应用于实际的升余弦滤波器。
2.系统模型
2.1.信道带宽无限时单极性基带传输
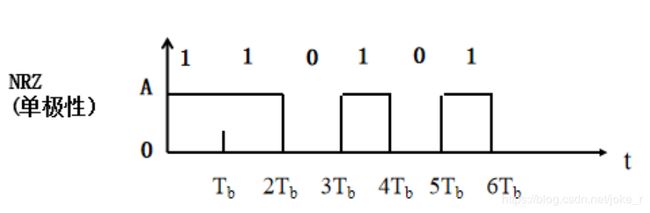
单极性码如图1所示,可看出幅度值:
a 1 = A ; a 2 = 0 ; \,\,a_{1}=A; a_{2}=0; a1=A;a2=0;
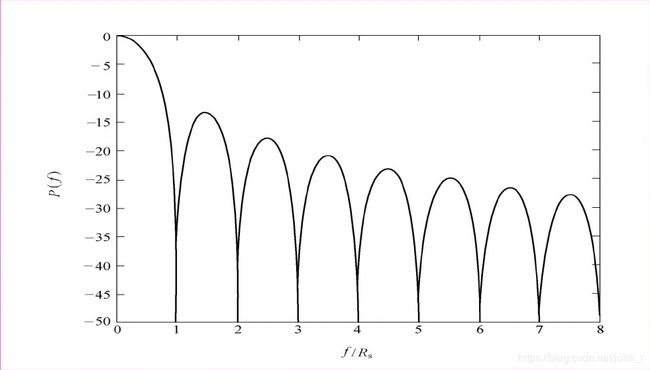
其中,发送滤波器冲激响应 g T ( t ) g_{T}(t) gT(t)为矩形不归零脉冲。其功率谱密度为:
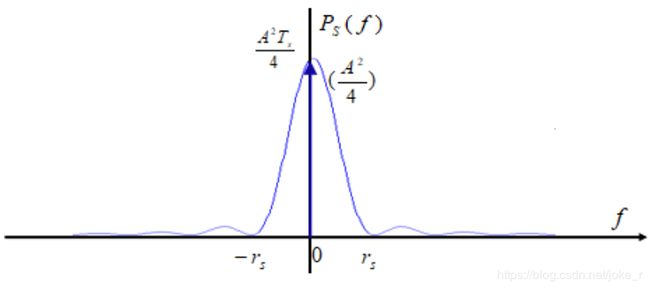
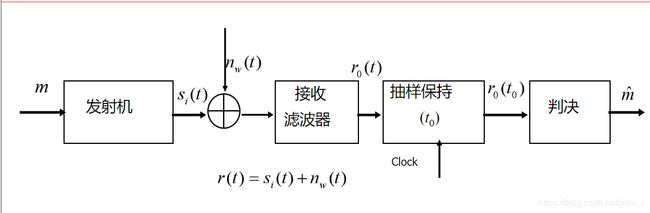
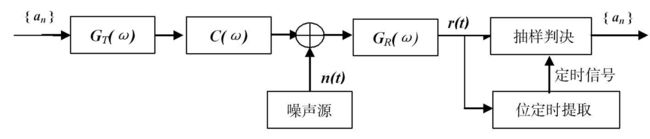
根据框图,可写出接收信号表达式为
1. r t ( f ) = s i ( t ) + n w ( t ) 1.\,\,r_{t}(f)=s_{i}(t)+n_{w}(t) 1.rt(f)=si(t)+nw(t)
如上文所述,为保证最佳接收,接收滤波器采用匹配滤波器,即:
2. h ( t ) = s 1 ( T b − t ) 2.\,\,h(t)=s_{1}(T_{b}-t) 2.h(t)=s1(Tb−t)
在采样时刻 t = T b t=T_{b} t=Tb,采样值中有用的信号是
3. ∫ 0 T b s 1 ( t ) h ( T b − t ) = E b 3.\,\,\int_{0}^{T_{b}}s_{1}(t)h(T_{b}-t)=E_{b} 3.∫0Tbs1(t)h(Tb−t)=Eb其中 E b E_b Eb称之为比特能量
而高斯白噪声通过匹配滤波器后的输出是平稳高斯过程,其方差为
4. δ 2 = N 0 2 E b 4.\,\, \delta^2=\frac{N_{0}}{2}E_{b} 4.δ2=2N0Eb
所以判决器输入的判决量为
5. y = E b + Z 5.\,\, y=E_{b}+Z 5.y=Eb+Z
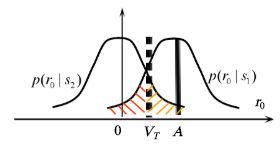
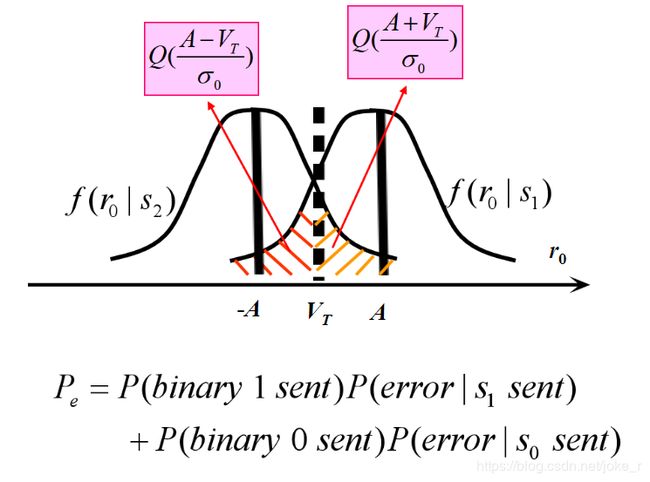
对于单极性不归零码来说,发 0 0 0和发 1 1 1的概率是相同的,都是50%。所以判决门限为
6. V T = E b 2 6.\,\, V_{T}=\frac{E_{b}}{2} 6.VT=2Eb
由上图,可以计算出误码率为:
7. P b = 1 2 e r f c ( E b 2 N 0 ) 7.\,\, P_{b}=\frac{1}{2}erfc(\sqrt \frac{E_{b}}{2N_{0}}) 7.Pb=21erfc(2N0Eb)
2.2.信道带宽受限时的双极性基带传输
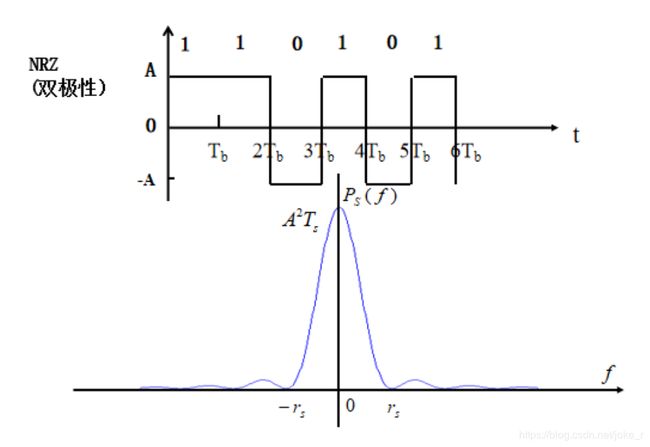
双极性极性码如图1所示,可看出幅度值:
a 1 = A ; a 2 = − A ; \,\,a_{1}=A; a_{2}=-A; a1=A;a2=−A;
二,基带传输接收系统模型:
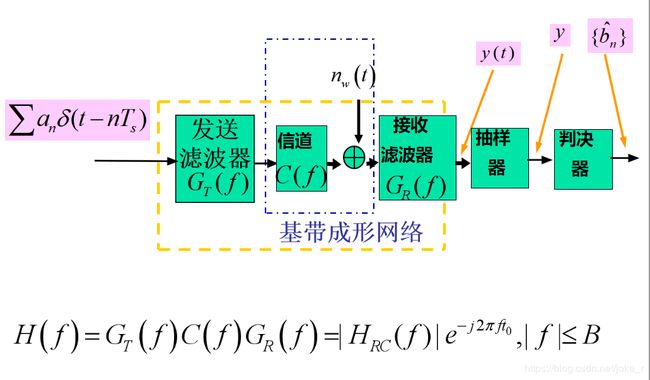
当信道带宽受限时,不能使用矩形脉冲作为发送滤波器,因为此种滤波器在频域里面是波形无限延伸的。而带宽却是有限的,势必会截取成有限长度的频谱波形,就会导致损失一部分信息。所以需要采用升余弦滤波器。
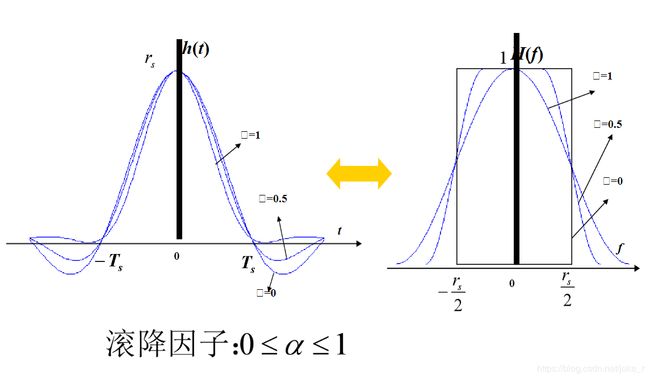
其系统函数为, 8. h ( t ) = s a ( π t T s ) c o s ( α π t / T s ) 1 − 4 α 2 t 2 / T s 2 8.\,\,h(t)=sa( \frac{\pi t}{T_{s}} )\frac{cos(\alpha \pi t/T_{s})}{1-4\alpha^2 t^2 /T_{s}^2} 8.h(t)=sa(Tsπt)1−4α2t2/Ts2cos(απt/Ts)
在接收端采样时刻无码间干扰的条件下,最佳接收的接受滤波器应匹配于所接受的确定信号,使接收端采样时刻的信噪比最大。而接收到的确定信号的频谱仅取决于发送滤波器的特性。发送滤波器与接收滤波器的传递函数的模值要近似于根升余弦频谱,才可为最佳接收系统
较于单极性传输来说,双极性码只不过是判决门限变动了。对于双极性不归零码来说,如果发 0 0 0和发 1 1 1的概率是相同的,都是50%。那么判决门限为
V T = 0 \,\, V_{T}=0 VT=0由此,误码率也随之发生变化为 9. P b = 1 2 e r f c ( E b N 0 ) 9.\,\, P_{b}=\frac{1}{2}erfc(\sqrt \frac{E_{b}}{N_{0}}) 9.Pb=21erfc(N0Eb)
2.3.信道带宽受限时QPSK传输
一,QPSK信号:
四进制移相键控(QPSK)又名四进制移相键控,该信号的正弦载波有4个可能的离散相位状态,每个载波相位携带2个二进制符号,其信号的表达式为:
s i ( t ) = A c o s ( w c t + θ i ) i = 1 , 2 , 3 , 4 0 ⩽ t ⩽ T s \,\,s_{i}(t)=Acos(w_{c}t+\theta_{i})\ \ \ \ i=1,2,3,4 \ \ \ \ \ 0\leqslant t \leqslant T_{s} si(t)=Acos(wct+θi) i=1,2,3,4 0⩽t⩽Ts
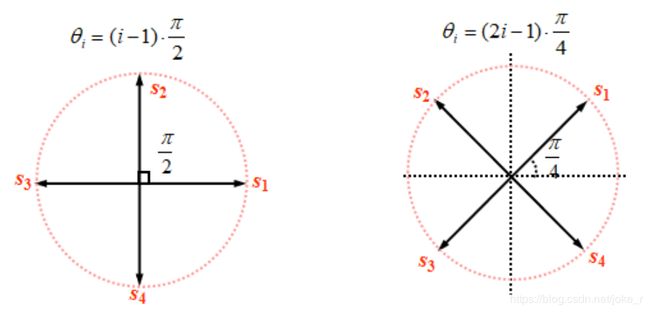
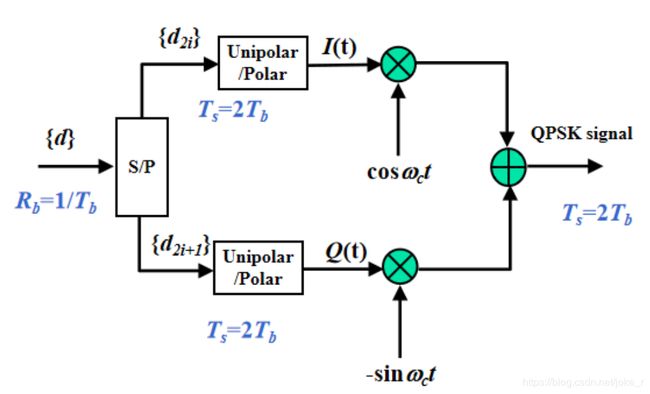
从上图可看出二进制序列 d ( n ) d(n) d(n)经串并变换后得到两路波形,再分别对正交载波 c o s w c t cosw_{c}t coswct及 − s i n w c t -sinw_{c}t −sinwct进行2PSK调制,再将这两路的2PSK信号相加即可得到QPSK信号。
由于QPSK信号可以看为同相及正交支路2PSK的叠加,所以在解调时可对两路信号分别进行2PSK解调,然后进行串并变换,得到输出数据。
在接收端采样时刻无码间干扰的条件下,最佳接收的接受滤波器应匹配于所接受的确定信号,使接收端采样时刻的信噪比最大。而接收到的确定信号的频谱仅取决于发送滤波器的特性,所以发送滤波器与接收滤波器的传递函数的模值要近似于根升余弦频谱,才可为最佳接收系统。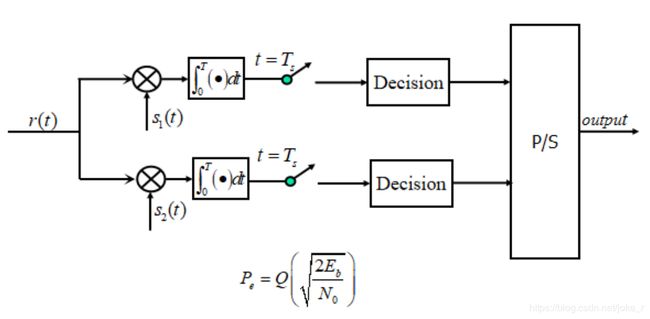
对于QPSK信号来说,在输入二进制信息速率相同,二者的发送功率相同,加性噪声的的单边功率谱密度 N 0 N_{0} N0相同情况下,实际误码率是和2PSK的平均误码率相同的,为 10. P b = 1 2 e r f c ( E b N 0 ) 10.\,\, P_{b}=\frac{1}{2}erfc(\sqrt \frac{E_{b}}{N_{0}}) 10.Pb=21erfc(N0Eb)其中 E b = A 2 2 T b , E_{b }=\frac{A^2}{2}T_{b}, Eb=2A2Tb,是平均比特能量。
2.4.信道带宽受限时16QAM传输
一,QPSK信号:
其信号的表达式为:
s Q A M ( t ) = a i c g T ( t ) c o s ( w c t ) − a i s g T ( t ) s i n ( w c t ) i = 1 , 2 , . . . , M 0 ⩽ t ⩽ T s \,\,s_{QAM}(t)=a_{i_{c}}g_{T}(t)cos(w_{c}t)-a_{i_{s}}g_{T}(t)sin(w_{c}t)\ \ \ \ i=1,2,...\ ,M \ \ \ \ \ 0\leqslant t \leqslant T_{s} sQAM(t)=aicgT(t)cos(wct)−aisgT(t)sin(wct) i=1,2,... ,M 0⩽t⩽Ts
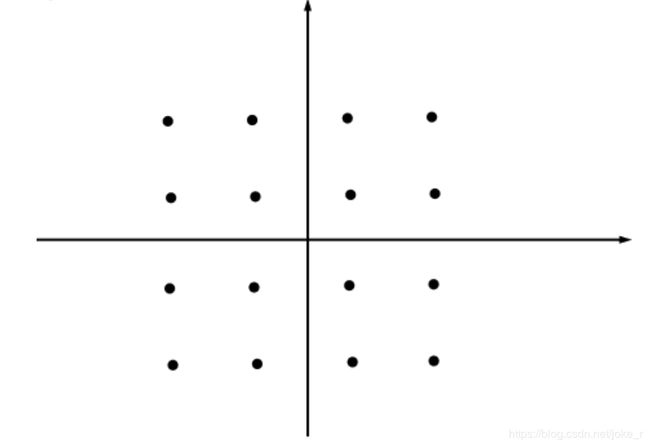
正交幅度调制(QAM)是由两个正交载波的多电平振幅键控信号叠加而成的。它是用两个独立的基带数字信号对两个互相正交的同频载波进行抑制在播的双边带调制,利用这种已调信号在同一带宽内频谱正交的性质来实现两路并行的数字信息传输。
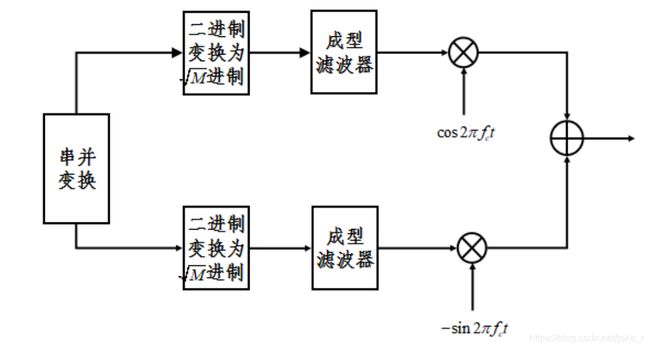
从上图可看出二进制序列 d ( n ) d(n) d(n)经串并变换。成形滤波后后得到两路 M \sqrt M M进制PAM信号,再分别对正交载波 c o s w c t cosw_{c}t coswct及 − s i n w c t -sinw_{c}t −sinwct进行 M \sqrt M M进制ASK调制,再将这两路信号相加即可得到QAM信号。
二,频带传输模型:
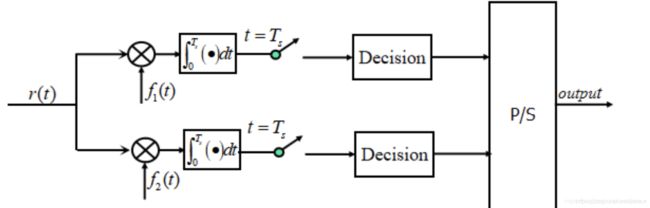
如图所示,对于该信号分别按同相与正交支路的 M \sqrt M MASK解调,在采样、判决后经串并变换恢复数据。
在接收端采样时刻无码间干扰的条件下,最佳接收的接受滤波器应匹配于所接受的确定信号,使接收端采样时刻的信噪比最大。而接收到的确定信号的频谱仅取决于发送滤波器的特性,所以发送滤波器与接收滤波器的传递函数的模值要近似于根升余弦频谱,才可为最佳接收系统。
MQAM的最佳接收误符率与MASK的一样,取决于数字基带MPAM的误符率。MQAM的正确判决符号概率为 11. P c = ( 1 − P M ) 2 11.\,\, P_{c}=(1-P_{\sqrt M})^2 11.Pc=(1−PM)2式中, P M P_{\sqrt M} PM表示同相或者正交支路 M \sqrt M M进制ASK的误符率。由此可得MQAM误码率为
12. P M ≈ 4 ( 1 − 1 M ) Q ( 3 E s ( M − 1 ) N 0 ) 12.\,\, P_{M}\approx4(1-\frac{1}{\sqrt M})Q(\sqrt \frac{3E_{s}}{(M-1)N_{0}}) 12.PM≈4(1−M1)Q((M−1)N03Es)
3.仿真过程与仿真结果分析
3.1 信道带宽无限时单极性传输系统
1.基础设置
clear all;close all
%------------------
%系统参数设置
%-----------------
T_start=0;%开始时间
T_stop=10;%截止时间
T=T_stop-T_start;%仿真持续时间
T_sample=1/1000;%采样间隔
f_sample=1/T_sample; % 采样速率
N_sample=T/T_sample;% 采样点数
n=0:N_sample-1;
r_s=100;%码元传输速率
NumBits=T*r_s;%传输符号总数
Tb=f_sample/r_s;%符号间隔
%-------------------------------
%产生单极性码基带信号
%-------------------------------
g_T=boxcar(Tb);%发送滤波器--矩形不归零脉冲
b1=rand(1,1000);b1(b1>0.5)=1;b1(b1<=0.5)=0;%初始序列
b2=zeros(f_sample/r_s,NumBits);
b2(1,:)=b1;%b1的值的赋给b2的第一行从开始到结束。
b3=reshape(b2,1,f_sample/r_s*NumBits);%reshape函数变换特定矩阵,此处是把b2转换成了一维矩阵
s=conv(b3,g_T);%发送信号
syms n;
Eb1=int(g_T,n,0,Tb);
n=0:N_sample-1;
Eb=sum(Eb1);
%--------------------------------
%产生噪声信号
%--------------------------------
N_0=10^(-3);
noise_w=wgn(1,length(s),N_0*f_sample,'linear');%产生一个m行n列的高斯白噪声的矩阵,p以dBW为单位指定输出噪声的强度。
r=s+noise_w;
figure(1)
%plot(s)
%hold on
plot(r)
title('发送信号r(t)时域波形');
ylabel('幅度');
%--------------------------------
%接收信号
%--------------------------------
g_R=boxcar(Tb);%匹配滤波器--实际和发送滤波器一样
y1=conv(r,g_R);
myeyediagram=eyediagram(y1,1*f_sample/r_s);%绘制眼图
title('眼图');
figure(3)
plot(y1)
title('接收信号y1(t)时域波形');
ylabel('幅度');
%设置采样序列
NumCoff=10;%采样起始位置
sample1=zeros(f_sample/r_s,NumBits);%抽样间隔为f_sample/r_s个点数
sample1(1,:)=ones(1,NumBits);
sample2=reshape(sample1,1,f_sample/r_s*NumBits);
sample3=zeros(1,length(y1));
sample3(NumCoff+1:NumCoff+f_sample/r_s*NumBits)=sample2;%得到采样序列函数
%plot(sample3)
%抽样判决
y2=y1.*sample3;%采样
y2(:,all((y2==0),1))=[];%删除y2中为0元素,返回矩阵给y2
b_t=b1;
b_r(y2>5)=1;b_r(y2<=5)=0;%判决并取值
BER=length(find(b_t~= b_r))/NumBits;
fprintf(' 误码率=%f',BER);
figure(4)
%误码率曲线图
EbN0_dB = 0:0.1:18;
Eb_N0 = 10.^(EbN0_dB/10);
Eb_N0=(1/2)*Eb_N0;
BER = 1/2.*erfc(sqrt(Eb_N0));
semilogy(EbN0_dB,BER)
axis([0,15,0.0000001,1]);
ylabel('误码率')
xlabel('E_b/N_0 (dB)')
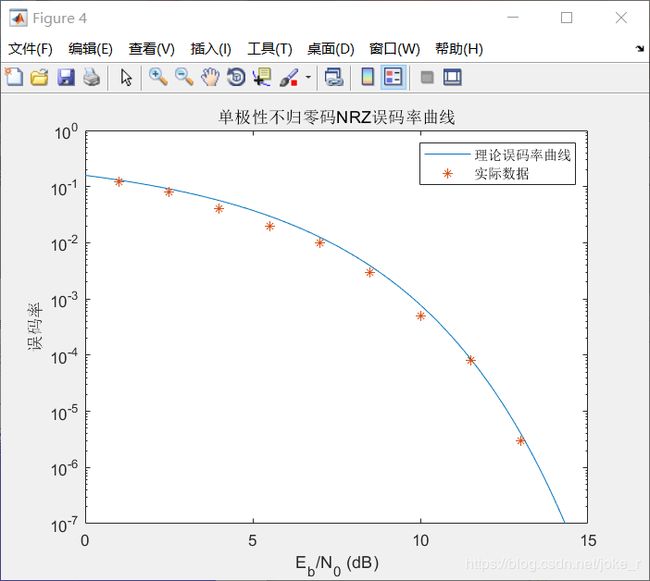
title('单极性不归零码NRZ误码率曲线')
hold on
%实际
x1=[1 2.5 4 5.5 7 8.5 10 11.5 13 15];
y1=[0.12 0.08 0.04 0.02 0.01 0.003 0.0005 0.00008 0.000003 0.00000001];
%figure (5)
semilogy(x1,y1,'*')%原来的折线
legend('理论误码率曲线','实际数据');
运行结果如下:
可以从上图看出,发送信号由于叠加噪声,导致波形出现些许微小起伏,不过噪声功率相比较小,所以对信号波形影响不大。
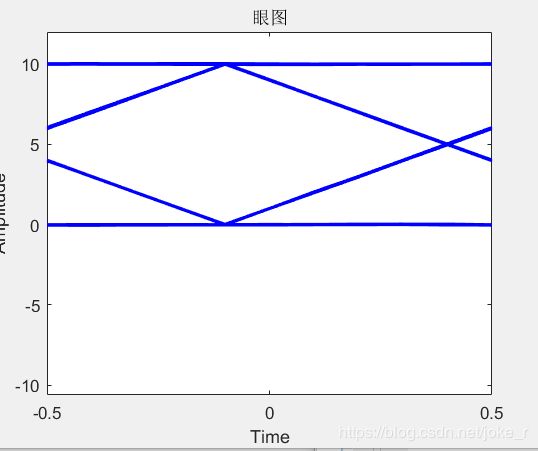
可以看出,眼睛睁开较大,推断出误码率较小,并且眼图中间横轴位置对应于判决门限 V T V_{T} VT为5
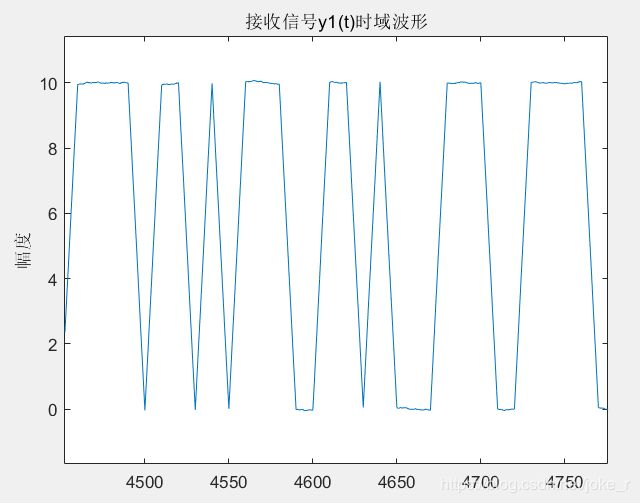
4.分析
由仿真结果可得,单极性基带传输采用矩形脉冲发送,经匹配滤波器解调后可的较好波形。计算误码率如上图所示为0.且由眼图可以看出“眼睛”张开程度较大,说明系统的误码不严重,与理论相符合。可以说明匹配滤波器作为最佳接收可以有较好的性能。
3.2 信道带宽受限时双极性传输系统
MATLAB 源码为:
clear all;close all
%------------------
%系统参数设置
%-----------------
T_start=0;%开始时间
T_stop=10;%截止时间
T=T_stop-T_start;%仿真持续时间
T_sample=1/1000;%采样间隔
f_sample=1/T_sample; % 采样速率
N_sample=T/T_sample;% 采样点数
n=0:N_sample-1;
r_s=100;%码元传输速率
alpha=0.25;%df=alpha*rs=25Hz
NumBits=T*r_s;%传输符号个数
NumCoff=40;%number of coefficients of RRC
%-------------------------------
%发送端
%-------------------------------
g_T=firrcos(NumCoff,r_s/2,alpha*r_s,f_sample);%发送滤波器--升余弦滤波器
b1=rand(1,1000);b1(b1>0.5)=1;b1(b1<=0.5)=-1;%双极性码
b2=zeros(f_sample/r_s,NumBits);
b2(1,:)=b1;%b1的值的赋给b2的第一行从开始到结束。
b3=reshape(b2,1,f_sample/r_s*NumBits);%reshape函数变换特定矩阵,此处是把b2转换成了一维矩阵
s=conv(b3,g_T);%发送信号
%--------------------------------
%噪声通道
%--------------------------------
N_0=10^(-6);
noise_w=wgn(1,length(s),N_0*f_sample,'linear');%产生一个m行n列的高斯白噪声的矩阵,p以dBW为单位指定输出噪声的强度。
r=s+noise_w;
figure(1)
subplot(2,1,1)
plot(s)
title('发送信号s(t)时域波形');
ylabel('幅度');
subplot(2,1,2)
plot(r)
title('接收信号r(t)时域波形');
ylabel('幅度');
%--------------------------------
%解调
%--------------------------------(1:length(y1))
g_R=firrcos(NumCoff,r_s/2,alpha*r_s,f_sample);%接收滤波器
y1=conv(r,g_R);
myeyediagram=eyediagram(y1,1*f_sample/r_s);
figure(3)
plot(y1)
title('解调信号y1(t)时域波形');
ylabel('幅度');
%hold on
NumCoff=40;%number of coefficients of RRC
SamplingIns=NumCoff/2;
SamplingStart=NumCoff;
sample1=zeros(f_sample/r_s,NumBits);%抽样间隔为f_sample/r_s个点数
sample1(1,:)=ones(1,NumBits);
sample2=reshape(sample1,1,f_sample/r_s*NumBits);
sample3=zeros(1,length(y1));
sample3(NumCoff+1:NumCoff+f_sample/r_s*NumBits)=sample2;
%plot(sample3)
y2=y1.*sample3;
y2(:,all((y2==0),1))=[];%B = all(A, 1)返回一个行向量,可以认为all(A, 1)等价于all(A)
b_t=b1;
b_r(y2>0)=1;b_r(y2<=0)=-1;%判决并取值
BER=length(find(b_t~= b_r))/NumBits;
fprintf(' 误码率=%f',BER);
%误码率曲线图
figure(4)
EbN0_dB = 0:0.1:18;
Eb_N0 = 10.^(EbN0_dB/10);
%Eb_N0=(1/2)*Eb_N0;
BER = 1/2.*erfc(sqrt(Eb_N0));
semilogy(EbN0_dB,BER)
axis([0,15,0.0000001,1]);
ylabel('误码率')
xlabel('E_b/N_0 (dB)')
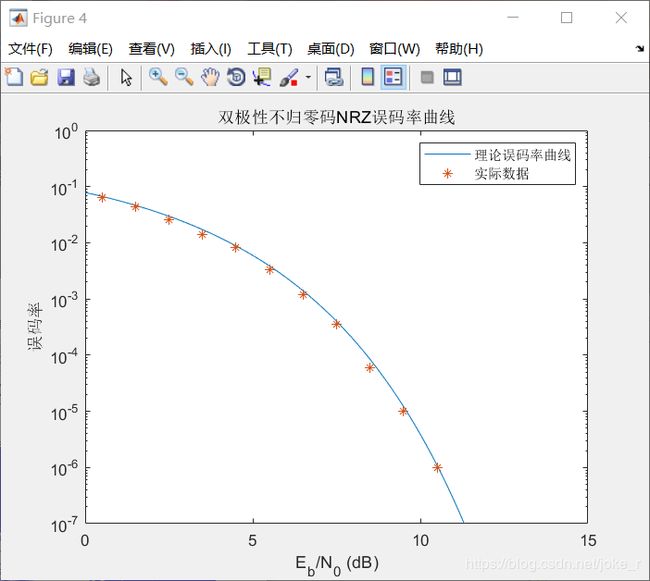
title('双极性不归零码NRZ误码率曲线')
hold on
%----------------------
x1=[0.5 1.5 2.5 3.5 4.5 5.5 6.5 7.5 8.5 9.5 10.5 11.5];
y1=[0.063 0.043 0.026 0.014 0.0084 0.0033 0.0012 0.00035 0.00006 0.00001 0.000001 0.00000005];
%figure (5)
semilogy(x1,y1,'*')%原来的折线
legend('理论误码率曲线','实际数据');
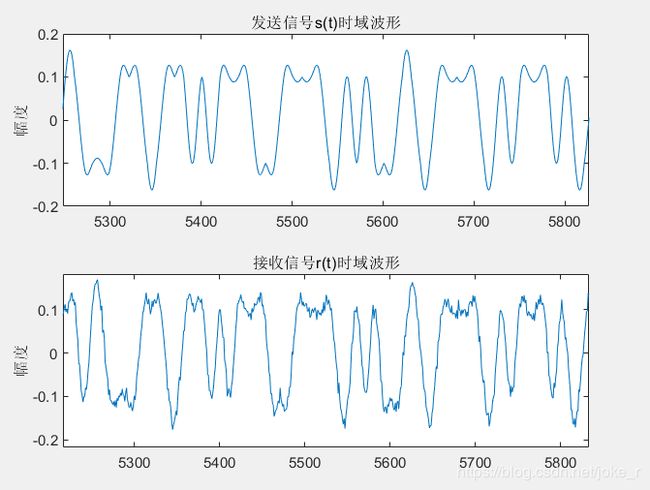
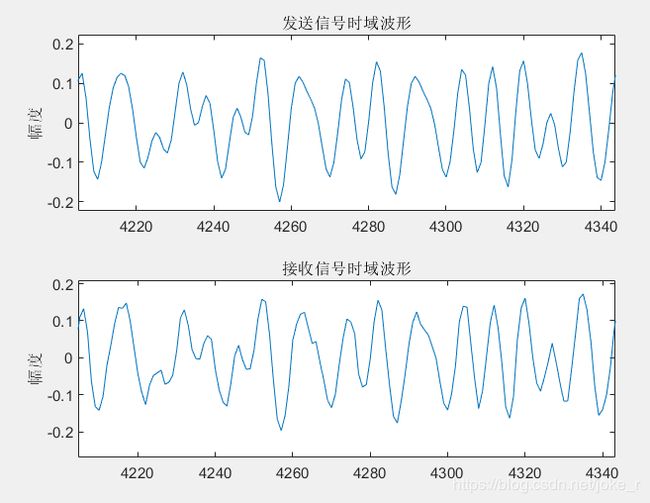
结果如下:
可以从上图看出,发送信号由于叠加噪声,导致波形出现些许微小起伏,不过噪声功率相比较小,所以对信号波形影响不大。
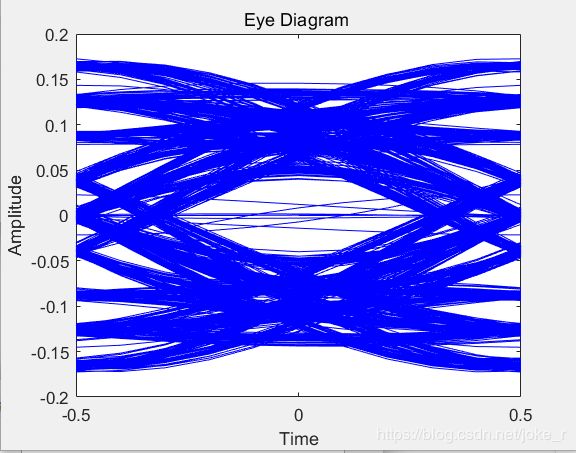
可以看出,眼睛睁开,推断出误码率较小,并且眼图中间横轴位置对应于判决门限 V T V_{T} VT为0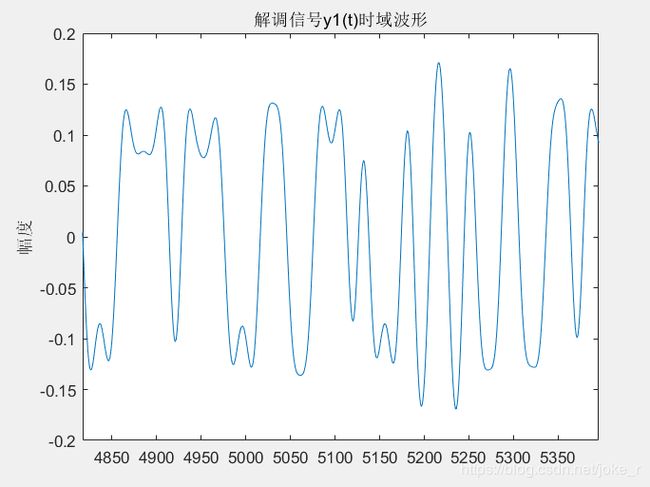
分析:当带宽有限时,我们就得考虑数字基带信号在通过限带线性滤波传输时,由于限带线性滤波器冲激响应不限时,其有限时间将延伸若干码元间隔,也就是所谓的码间干扰。为避免此影响,所以发送滤波器和接收滤波器相匹配基础上,还得满足升余弦滤波器。从仿真角度看,误码率为0,眼图睁开。但理论上相比单极性,双极性误码率更小。
3.3 信道带宽受限时QPSK传输系统
MATLAB 源码:
clear all;close all
%------------------
%系统参数设置
%-----------------
T_start=0;%开始时间
T_stop=10;%截止时间
T=T_stop-T_start;%仿真持续时间
T_sample=1/1000;%采样间隔
f_sample=1/T_sample; % 采样速率
N_sample=T/T_sample;% 采样点数
n=0:N_sample-1;
r_s=100;%码元传输速率
alpha=0.25;%df=alpha*rs=25Hz
NumBits=T*r_s;%传输符号个数
NumCoff=40;%number of coefficients of RRC
%-------------------------------
%Transmitter
%-------------------------------
g_T=firrcos(NumCoff,r_s/2,alpha*r_s,f_sample);%发送滤波器--升余弦滤波器
b=rand(1,2000);b(b>0.5)=1;b(b<=0.5)=-1;
a=b;
%串并变换
b_2n=a(:,2:2:end);%取偶数列--同相支路
b_2n_1=b(:,1:2:end);%取奇数列--正交支路
%同相支路调制
b2=zeros(f_sample/r_s,NumBits);
b2(1,:)=b_2n;%b1的值的赋给b2的第一行从开始到结束。
b3=reshape(b2,1,f_sample/r_s*NumBits);%reshape函数变换特定矩阵,此处是把b2转换成了一维矩阵
s_2n=conv(b3,g_T);%发送信号1
fc=100;
k=0:N_sample-1+NumCoff;
c1=cos(2*pi*fc*k*T_sample);
s_2n=s_2n.*c1;
%--------------------------------
%正交支路调制
b2=zeros(f_sample/r_s,NumBits);
b2(1,:)=b_2n_1;%b1的值的赋给b2的第一行从开始到结束。
b3=reshape(b2,1,f_sample/r_s*NumBits);%reshape函数变换特定矩阵,此处是把b2转换成了一维矩阵
s_2n_1=conv(b3,g_T);%发送信号1
fc=100;
k=0:N_sample-1+NumCoff;
c2=-sin(2*pi*fc*k*T_sample);
s_2n_1=s_2n_1.*c2;
%-发送信号
s=s_2n+s_2n_1;
%----绘图
figure(1)
subplot(2,1,1)
plot(s_2n)
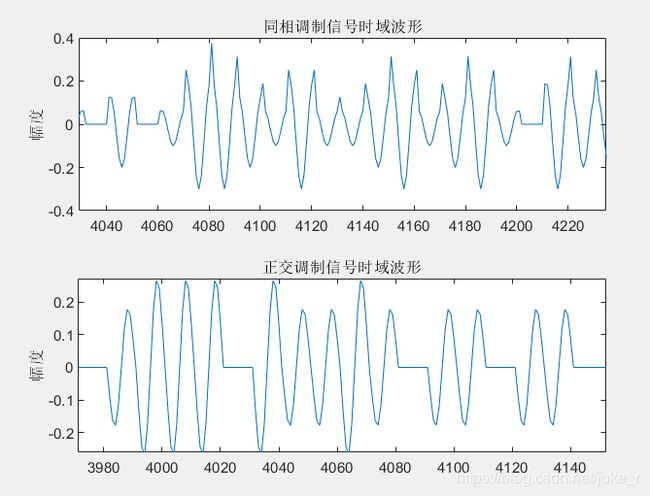
title('同相调制信号时域波形');
ylabel('幅度');
subplot(2,1,2)
plot(s_2n_1)
title('正交调制信号时域波形');
ylabel('幅度');
%噪声
%--------------------------------
N_0=10^(-7);
noise_w=wgn(1,length(s),N_0*f_sample,'linear');%产生一个m行n列的高斯白噪声的矩阵,p以dBW为单位指定输出噪声的强度。
r=s+noise_w;
figure(2)
subplot(2,1,1)
plot(s)
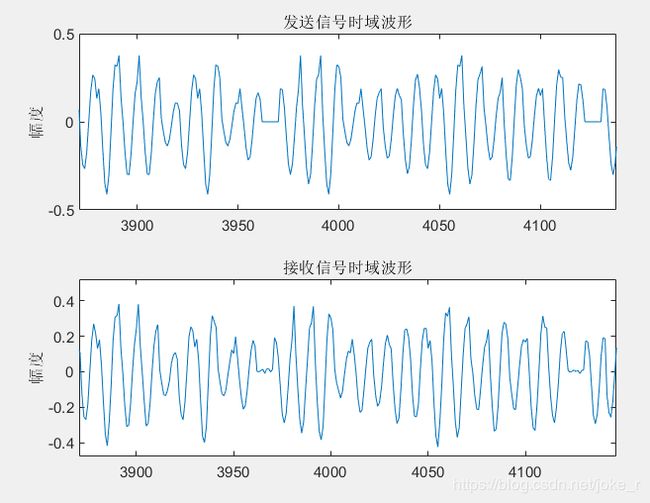
title('发送信号时域波形');
ylabel('幅度');
subplot(2,1,2)
plot(r)
title('接收信号时域波形');
ylabel('幅度');
%receiver
%--------------------------------
g_R=firrcos(NumCoff,r_s/2,alpha*r_s,f_sample);%接收滤波器
%同相支路解调
x_2n=r.*c1;
x_2n=conv(x_2n,g_R);
myeyediagram1=eyediagram(x_2n,1*f_sample/r_s);
%--------------------------------
%正交支路解调
x_2n_1=r.*c2;
x_2n_1=conv(x_2n_1,g_R);
myeyediagram2=eyediagram(x_2n_1,1*f_sample/r_s);
%--------------------------------
%myeyediagram=eyediagram(x_2n_1+x_2n,1*f_sample/r_s);
%--------------------------------
NumCoff=40;%number of coefficients of RRC
SamplingIns=NumCoff/2;
SamplingStart=NumCoff;
sample1=zeros(f_sample/r_s,NumBits);%抽样间隔为f_sample/r_s个点数
sample1(1,:)=ones(1,NumBits);
sample2=reshape(sample1,1,f_sample/r_s*NumBits);
sample3=zeros(1,length(x_2n));
sample3(NumCoff+1:NumCoff+f_sample/r_s*NumBits)=sample2;
%plot(sample3)
% 同相抽样判决
y_2n=x_2n.*sample3;
y_2n(:,all((y_2n==0),1))=[];%B = all(A, 1)返回一个行向量,可以认为all(A, 1)等价于all(A)
b_r2n(y_2n>0)=1;b_r2n(y_2n<=0)=-1;%判决并取值
%正交抽样判决
y_2n_1=x_2n_1.*sample3;
y_2n_1(:,all((y_2n_1==0),1))=[];%B = all(A, 1)返回一个行向量,可以认为all(A, 1)等价于all(A)
b_r2n_1(y_2n_1>0)=1;b_r2n_1(y_2n_1<=0)=-1;%判决并取值
%并串转换
b_r(2,:)=b_r2n;%b1的值的赋给b2的第一行从开始到结束。
b_r(1,:)=b_r2n_1;
b_r=reshape(b_r,1,length(b));
%---------
b_t=sign(b);
BER=length(find(b_t~=b_r))/2000;
BER=length(find(b_t~= b_r))/NumBits;
fprintf(' 误码率=%f',BER);
%误码率曲线图
figure(5)
EbN0_dB = 0:0.1:18;
Eb_N0 = 10.^(EbN0_dB/10);
%Eb_N0=(1/2)*Eb_N0;
BER = 1/2.*erfc(sqrt(Eb_N0));
semilogy(EbN0_dB,BER)
axis([0,14,0.000001,0.1]);
ylabel('误码率')
xlabel('E_b/N_0 (dB)')
title('QPSK误码率曲线')
hold on
%----------------------
x1=[0.5 1.5 2.5 3.5 4.5 5.5 6.5 7.5 8.5 9.5 10.5 11.5];
y1=[0.064 0.043 0.027 0.015 0.0085 0.0036 0.001 0.00037 0.00008 0.00001 0.000001 0.00000005];
%figure (5)
semilogy(x1,y1,'*')%原来的折线
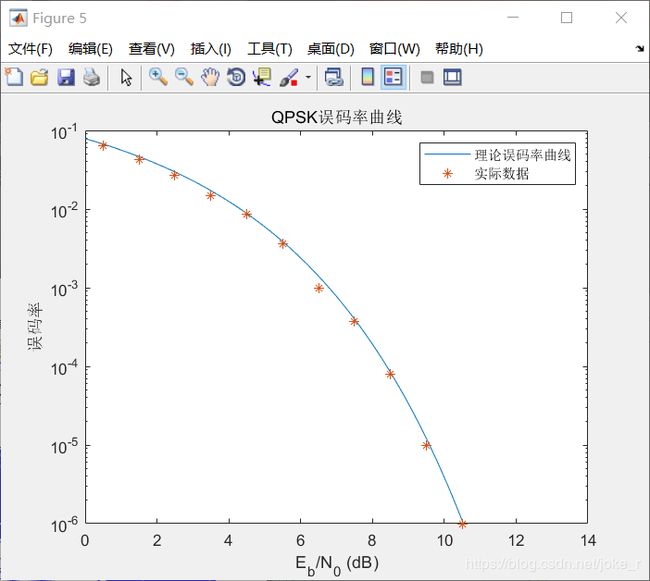
legend('理论误码率曲线','实际数据');
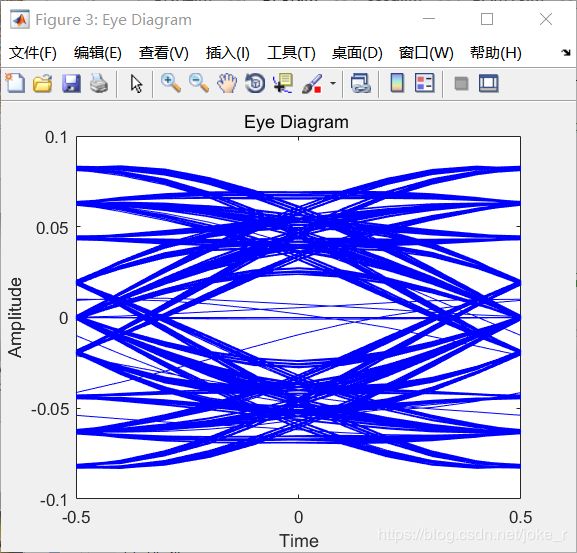
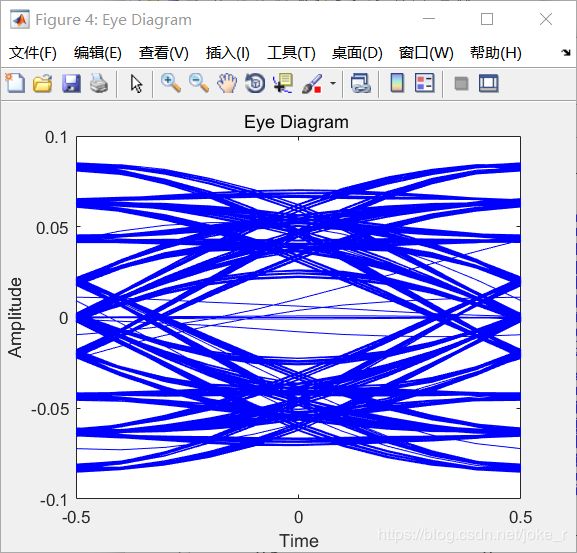
分析:QPSK调制从理论分析来看类似2PSK调制。实际上就是对两路信号分别做2PSK调制然后相加得到QPSK信号,不过由于载波不同,就正好形成了输出波形的相位逻辑关系。此关系正好符合格雷码相位逻辑关系。采用格雷码的时候,从四进制译成二进制码,可以减少误比特率。根据仿真结果两路的眼图都十分良好,误码率也十分良好
3.4 信道带宽受限时16QAM传输系统
MATLAB代码:
clear all;close all
%------------------
%系统参数设置
%-----------------
T_start=0;%开始时间
T_stop=10;%截止时间
T=T_stop-T_start;%仿真持续时间
T_sample=1/1000;%采样间隔
f_sample=1/T_sample; % 采样速率
N_sample=T/T_sample;% 采样点数
n=0:N_sample-1;
r_s=100;%码元传输速率
alpha=0.25;%df=alpha*rs=25Hz
NumBits=T*r_s;%传输符号个数
NumCoff=10;%number of coefficients of RRC
Tb=f_sample/r_s;
%-------------------------------
%Transmitter
%-------------------------------
g_T=firrcos(NumCoff,r_s/2,alpha*r_s,f_sample);%发送滤波器--升余弦滤波器
b=rand(1,4000);b(b>0.5)=1;b(b<=0.5)=0;%产生初始序列
%串并变换
a_2n=b(:,2:2:end);
a_2n_1=b(:,1:2:end);
%---二进制转四进制
a_2n_r1=reshape(a_2n,2,length(a_2n)/2);
a_2n_r2=reshape(a_2n_1,2,length(a_2n_1)/2);
b_r2n_1=rand(2,1000);
x2=rand(2,1000);
for i=1:1000
sym m;
m=a_2n_r1(1,i);
b_r2n_1(1,i)=m*(2.^m);
end
for i=1:1000
sym m;
m=a_2n_r1(2,i);
b_r2n_1(2,i)=m;
end
b_2n=sum(b_r2n_1);
for i=1:1000
sym m;
m=a_2n_r2(1,i);
x2(1,i)=m*(2.^m);
end
for i=1:1000
sym m;
m=a_2n_r2(2,i);
x2(2,i)=m;
end
b_2n_1=sum(x2);
%------------
%由于在最后一步由四进制转化为二进制这步还不能实现,
%故误码率是与原来转化成的四进制做对比
b_t(2,:)=b_2n;%b1的值的赋给b2的第一行从开始到结束。
b_t(1,:)=b_2n_1;
b_t1=reshape(b_t,1,length(b)/2);
%b_t1为四进制序列
%同相支路调制
b2=zeros(f_sample/r_s,NumBits);
b2(1,:)=b_2n;%b1的值的赋给b2的第一行从开始到结束。
b3=reshape(b2,1,f_sample/r_s*NumBits);%reshape函数变换特定矩阵,此处是把b2转换成了一维矩阵
s_2n=conv(b3,g_T);%同相支路发送信号
%与载波相乘
fc=100;
k=0:N_sample-1+NumCoff;
c1=cos(2*pi*fc*k*T_sample);
s_2n=s_2n.*c1;
%--------------------------------
%正交支路调制
b2=zeros(f_sample/r_s,NumBits);
b2(1,:)=b_2n_1;%b1的值的赋给b2的第一行从开始到结束。
b3=reshape(b2,1,f_sample/r_s*NumBits);%reshape函数变换特定矩阵,此处是把b2转换成了一维矩阵
s_2n_1=conv(b3,g_T);%正交支路发送信号
%与载波相乘
fc=100;
k=0:N_sample-1+NumCoff;
c2=-sin(2*pi*fc*k*T_sample);
s_2n_1=s_2n_1.*c2;
%------------figure(1)
subplot(2,1,1)
plot(s_2n)
title('同相调制信号时域波形');
ylabel('幅度');
subplot(2,1,2)
plot(s_2n_1)
title('正交调制信号时域波形');
ylabel('幅度');
%-------------------------------
s=s_2n+s_2n_1;%发送信号
%AWGN channel
%--------------------------------
N_0=10^(-7);
noise_w=wgn(1,length(s),N_0*f_sample,'linear');%产生一个m行n列的高斯白噪声的矩阵,p以dBW为单位指定输出噪声的强度。
r=s+noise_w;
figure(2)
subplot(2,1,1)
plot(s)
title('发送信号时域波形');
ylabel('幅度');
subplot(2,1,2)
plot(r)
title('接收信号时域波形');
ylabel('幅度');
%--------------------------------
%receiver
%-------------------------------
g_R=firrcos(NumCoff,r_s/2,alpha*r_s,f_sample);%接收滤波器
%-------------------------------
%同相解调
x_2n=r.*c1;
x_2n=conv(x_2n,g_R);
myeyediagram1=eyediagram(x_2n,1*f_sample/r_s);
%--------------------------------
%正交解调
x_2n_1=r.*c2;
x_2n_1=conv(x_2n_1,g_R);
myeyediagram2=eyediagram(x_2n_1,1*f_sample/r_s);
%--------------------------------
figure (5)
subplot(2,1,1)
plot(x_2n)
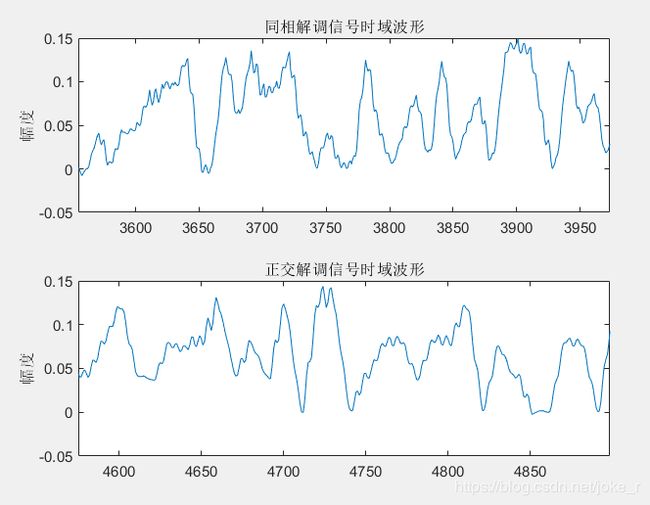
title('同相解调信号时域波形');
ylabel('幅度');
subplot(2,1,2)
plot(x_2n_1)
title('正交解调信号时域波形');
ylabel('幅度');
NumCoff=10;%number of coefficients of RRC
SamplingIns=NumCoff/2;
SamplingStart=NumCoff;
sample1=zeros(f_sample/r_s,NumBits);%抽样间隔为f_sample/r_s个点数
sample1(1,:)=ones(1,NumBits);
sample2=reshape(sample1,1,f_sample/r_s*NumBits);
sample3=zeros(1,length(x_2n));
sample3(NumCoff+1:NumCoff+f_sample/r_s*NumBits)=sample2;
%plot(sample3)
%2n 抽样
y_2n=x_2n.*sample3;
y_2n(:,all((y_2n==0),1))=[];%B = all(A, 1)返回一个行向量,可以认为all(A, 1)等价于all(A)
%根据眼图做出判决
%同相支路判决
b_r2n=rand(1,1000);
for i=1:1000
sym m;
sym n;
m=y_2n(i);
if(m>0.107)
b_r2n(i)=3;
else if(m>0.072)
b_r2n(i)=2;
else if(m>0.03)
b_r2n(i)=1;
else
b_r2n(i)=0;
end
end
end
end
%正交支路判决
y_2n_1=x_2n_1.*sample3;
y_2n_1(:,all((y_2n_1==0),1))=[];%B = all(A, 1)返回一个行向量,可以认为all(A, 1)等价于all(A)
b_r2n_1=rand(1,1000);
for i=1:1000
sym m;
sym n;
m=y_2n_1(i);
if(m>0.10)
b_r2n_1(i)=3;
else if(m>0.062)
b_r2n_1(i)=2;
else if(m>0.025)
b_r2n_1(i)=1;
else
b_r2n_1(i)=0;
end
end
end
end
%并串转换
b_r(2,:)=b_r2n;%b1的值的赋给b2的第一行从开始到结束。
b_r(1,:)=b_r2n_1;
b_r=reshape(b_r,1,length(b)/2);
%---------
b_t=sign(b);
BER1=length(find(b_t1~=b_r))/2000;
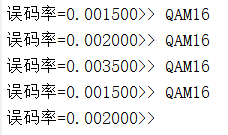
fprintf('误码率=%f',BER1);
%误码率曲线图
figure(6)
EbN0_dB = 0:0.1:25;
Eb_N0 = 10.^(EbN0_dB/10);
Eb_N0=(1/3)*Eb_N0;
BER = 1/2.*erfc(sqrt(Eb_N0));
BER=(2)*BER;
semilogy(EbN0_dB,BER)
axis([-6,22,0.000001,0.1]);
ylabel('误码率')
xlabel('E_b/N_0 (dB)')
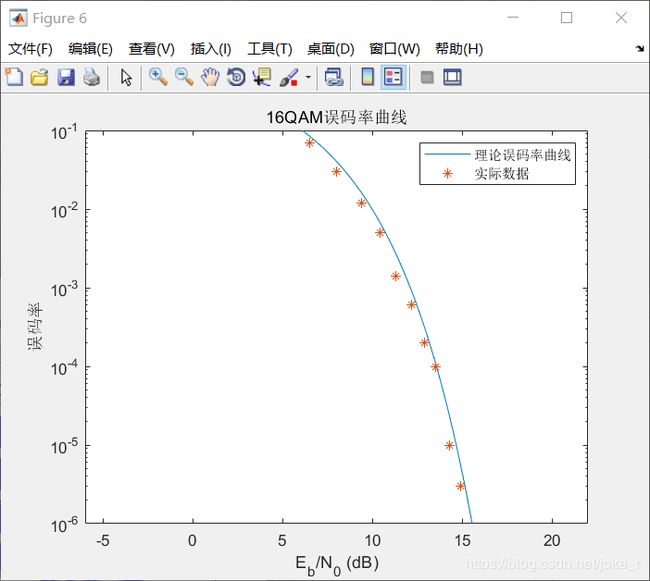
title('16QAM误码率曲线')
hold on
%----------------------
x1=[6.5 8 9.4 10.4 11.3 12.2 12.9 13.5 14.3 14.9 15.5];
y1=[0.07 0.03 0.012 0.005 0.0014 0.0006 0.0002 0.0001 0.00001 0.000003 0.0000008];
%figure (5)
semilogy(x1,y1,'*')%原来的折线
legend('理论误码率曲线','实际数据');
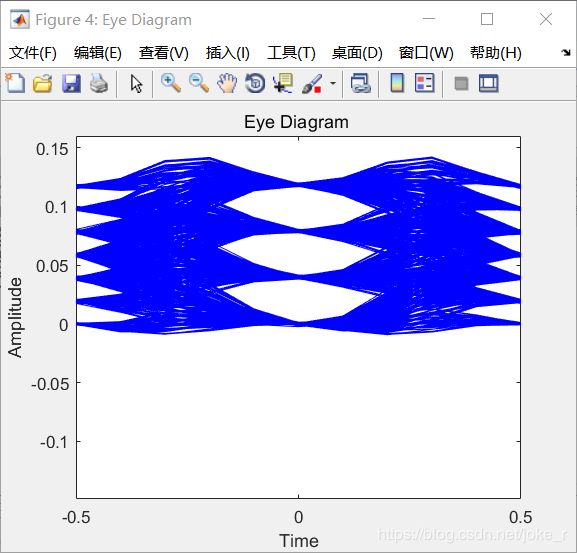
仿真结果:
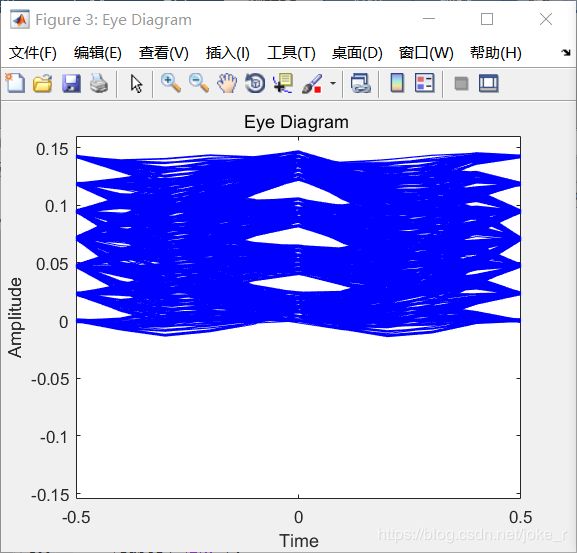
分析:16QAM信号是为联合控制了正弦载波幅度及相位的数字调制信号。可看作是4PAM与4ASK共同进行调制的信号。所以有 4 × 4 = 16 4\times 4=16 4×4=16 种信号变化。幅度四种,相位四种。仿真眼图看上去不太理想,张开的幅度比较小。所以,误码率也就不再为零了。
4.小结
上文的四个模拟仿真分别对应了基带,频带,相位调制,幅度调制,相位暨幅度调制。基带信号与频带信号的区别就是,在发送端乘上了一个正弦函数,使其搬移到高频处方便传输。同时发送滤波器必须近似为为理想低通滤波器,让发送信号变成一个带限信号以便于在带宽有限的信道上传输。除此之外,就是类似于模拟信号的幅度调制和角度调制了。这里只模拟了幅度和相位调制,频率调制则没有。
除此之外,无论带宽有限还是无限,基带还是频带我们都需要采用最佳接收方式,也就是接收滤波器和发送滤波器相匹配,或者采用相干解调方式。二者本质上一样。
通过这次仿真,深刻的了解到了单极性码和双极性码的区别,在于误码率和发送信号功率的抉择。同时也了解到为什么QPSK要用格雷码来转换二进制码,是为了降低误比特率。同时知晓了,同时也熟悉了QPSK与16QAM信号,发现矩形星座QAM最佳接收误符率与MASK的一样,取决于数字基带MPAM的误符率,而QPSK与2PSK的输入二进制信息速率相同的情况下,二者的发送功率相同,QPSK与2PSK的平均误码率也是相同的。