第七周工作总结——接收信号同步

1. 总述

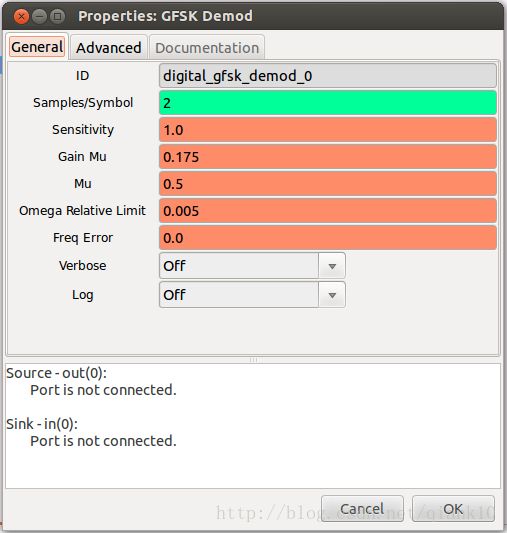
尽管Gnuradio提供了gfsk解调block，但是该block提供了许多貌似与解调无关的参数，block的属性窗口如下：

图中的Sample/Symbol参数指示了信号中每个码元的采样数；而sensitivity则用于指示解调的相位分辨率。而剩余四个参数（Gain Mu, Mu, Omega Relative Limit以及Freq Error）的用途就不那么清楚了。通过分析gfsk解调block的实现，我了解到该block在对gfsk信号解调之前，对信号进行了时钟和频率同步，上述四个参数即用于时钟同步。

2. 同步

无线通信的发射接收机之间往往是不同步的，包括时钟对齐、载波频率、采样等都具有一定的误差，这就导致接收机接收的信号产生了失真。因此接收机的主要工作之一就是消除这些误差，恢复原始信号。

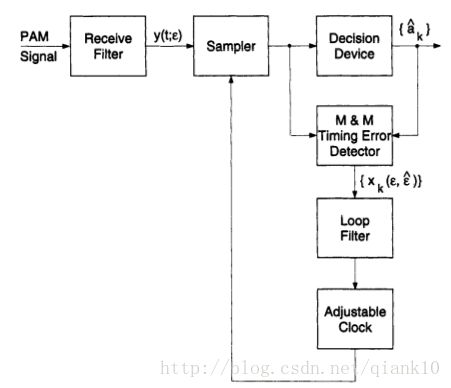
采用不同调制手段生成的信号，其接收端的同步算法往往是不同的，对于gfsk调制的离散信号而言，最合适的同步算法就是Mueller and Muller (M&M)算法。M&M同步算法是离散时间错误追踪（discrete-time, error-tracking）的算法，其原理图如下：

其中y是接收信号，一般数字信号的解调过程即为采样和判决，判决设备的输出a即为码元符号。当然，同步误差会降低判决的正确率，因此需要同步算法对其进行消除，而对同步误差的估计可以从采样设备输出和判决设备输出中得到。M&M算法的核心即通过采样输出和判决输出的线性组合指示同步误差的大小，该指示值将被反馈给采样设备，调整采样时钟，从而逐渐消除采样误差。关于M&M算法的参考文献如下：

[1] Digital Communication Receivers Synchronization, Channel Estimation, and Signal Processing
[2] Timing Recovery in Digital Synchronours Data Receivers

然而，SDR中信号的采样和对采样的操作是在不同的设备中完成的，信号采样通过外设（如HackRF one）中的ADC实现，而处理采样则是在其传输到PC后在Gnuradio中实现的，两者之间并没有反馈的功能（当然如果在外设的FPGA上编程也许可以实现反馈电路，这方面我没有接触过，并不了解）。这就导致上面的原理图中所示的反馈电路在SDR的框架下无法实现。

当然，Gnuradio的设计者给出了一种替代方案，既然SDR的采样无法改变，那就通过插值得到我们所需要的位置的采样，而这个位置是可以通过诸如M&M等同步算法确定的。这就是Gnuradio中实现gfsk信号同步的基本原理。

3. gfsk信号同步

下面介绍一下Gnuradio中的gfsk解调block的基本流程，block的主要实现代码如下：

        self._samples_per_symbol = samples_per_symbol
        self._gain_mu = gain_mu
        self._mu = mu
        self._omega_relative_limit = omega_relative_limit
        self._freq_error = freq_error
        self._differential = False
        
        if samples_per_symbol < 2:
            raise TypeError, "samples_per_symbol >= 2, is %f" % samples_per_symbol

        self._omega = samples_per_symbol*(1+self._freq_error)

        if not self._gain_mu:
            self._gain_mu = 0.175
            
        self._gain_omega = .25 * self._gain_mu * self._gain_mu 

	# Demodulate FM
	#sensitivity = (pi / 2) / samples_per_symbol
	self.fmdemod = analog.quadrature_demod_cf(1.0 / sensitivity)

	# the clock recovery block tracks the symbol clock and resamples as needed.
	# the output of the block is a stream of soft symbols (float)
	self.clock_recovery = digital.clock_recovery_mm_ff(self._omega, self._gain_omega,
                                                           self._mu, self._gain_mu,
                                                           self._omega_relative_limit)

        # slice the floats at 0, outputting 1 bit (the LSB of the output byte) per sample
        self.slicer = digital.binary_slicer_fb()

        if verbose:
            self._print_verbage()
         
        if log:
            self._setup_logging()

	# Connect & Initialize base class
	self.connect(self, self.fmdemod, self.clock_recovery, self.slicer, self)

Gnuradio中的gfsk解调block是一个复合block(hierarchical block)，复合block本质上是由多个block相连构成的不完整的流图。这里，gfsk解调block由三个子block构成，分别是quadrature_demod_cf、clock_recovery_mm_ff以及binary_slicer_fb。其中quadrature_demod_cf是调频解调模块，通过计算相邻采样的相位差（相当于求导）获得频率变化信息；clock_recovery_mm_ff是实现M&M算法的同步模块；而binary_slicer_fb则是二元判决模块，由于gfsk本质上是经过gaussian滤波的2fsk。下面介绍clock_recovery_mm_ff模块的具体实现，说明一下，这里的后缀ff表示该模块的输入输出都是浮点数，用以区别复数的情形。

clock_recovery_mm_ff的work函数如下：

int
    clock_recovery_mm_ff_impl::general_work(int noutput_items,
					    gr_vector_int &ninput_items,
					    gr_vector_const_void_star &input_items,
					    gr_vector_void_star &output_items)
    {
      const float *in = (const float *)input_items[0];
      float *out = (float *)output_items[0];

      int ii = 0; // input index
      int oo = 0; // output index
      int ni = ninput_items[0] - d_interp->ntaps(); // don't use more input than this
      float mm_val;

      while(oo < noutput_items && ii < ni ) {
	// produce output sample
	out[oo] = d_interp->interpolate(&in[ii], d_mu);
	mm_val = slice(d_last_sample) * out[oo] - slice(out[oo]) * d_last_sample;
	d_last_sample = out[oo];

	d_omega = d_omega + d_gain_omega * mm_val;
	d_omega = d_omega_mid + gr::branchless_clip(d_omega-d_omega_mid, d_omega_relative_limit);
	d_mu = d_mu + d_omega + d_gain_mu * mm_val;

	ii += (int)floor(d_mu);
	d_mu = d_mu - floor(d_mu);
	oo++;
      }

      consume_each(ii);
      return oo;
    }

我们可以看到参数mu, gain_mu, omega和gain_omega出现在上面的代码中，代码中的前缀d用于指明这些变量是私有的。从代码中我们可以大概知道这些参数的作用，mu是采样误差（-0.5~+0.5）；omega对应频率误差，当然，频率误差也体现在采样偏移上。代码中的mm_val变量即M&M算法得到的误差指示量：

	mm_val = slice(d_last_sample) * out[oo] - slice(out[oo]) * d_last_sample;

其中slice函数是简单的二元判决，out[oo]和d_last_sample分别是当前和上一个正确的采样值。而参数gain_mu和gain_omega分别是调节mu和omega时对mm_val进行加权的系数，这一点可以在代码中体现出来：

	d_omega = d_omega + d_gain_omega * mm_val;
	d_omega = d_omega_mid + gr::branchless_clip(d_omega-d_omega_mid, d_omega_relative_limit);
	d_mu = d_mu + d_omega + d_gain_mu * mm_val;

上述代码也为omega_relative_limit的作用提供了解释，开发者假设信号中的频率误差变化不大，一般在默认误差附近变化，且变化不会超过某个阈值，这个阈值就是omega_relative_limit。

综合考虑了时钟误差和频率误差后，我们可以计算出下一个采样的位置，由输入索引ii和采样偏移mu来确定：

	ii += (int)floor(d_mu);
	d_mu = d_mu - floor(d_mu);

这样，在下一次循环中，同步后的输出采样就可以通过插值滤波得到了：

out[oo] = d_interp->interpolate(&in[ii], d_mu);

现在只剩下了最后一个问题，即参数mu, omega, gain_mu和gain_omega是如何确定的？模块默认的参数值如下：

        mu = 0.5;
        gain_mu = 0.175;
        freq_error = 0.0;
        omega = samples_per_symbol * (1 + freq_error);
        gain_omega = 0.25 * gain_mu * gain_mu;
        omega_relative_limit = 0.005

• mu确定了采样误差的初始值，0.5对应了最差情况。
• freq_error定义了初始的频率误差，这里设为0。
• omega则是频率误差下造成的采样偏移。
• omega_relative_limit定义了omega的最大偏移值，为0.005。

上述几个参数的初始值我认为是比较合理的，至于gain_mu和gain_omega是如何确定的我就不太清楚了，如果有人知道这些值的来源，请帮忙指出，谢谢！