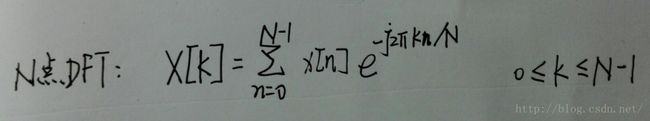DFT做频谱分析再理解
DFT再理解
2015.12.18
之前学习《信号与系统》的时候,对于用fft()函数分析离散、连续时间信号的频谱出来的结果一直一知半解,这学期学习了《数字信号处理》,学习了离散傅里叶变换(DFT),对之前的写的程序做进一步理解。
在此之前,先将CTFS、DTFS、CTFT、DTFT的公式列出来,方便理解:
注意:这里计算离散周期信号的傅里叶系数的公式前面少了一个N分之一,下面也会涉及到。
(一) 用DFT分析离散非周期信号的频谱(离散非周期的DTFT为连续周期的,以2*pi为周期)
比较DTFT和DFT公式可以发现:
N点DFT是DTFT结果在[0,2*pi]周期内N点采样;
所以,分析离散非周期信号的频谱的思路如下:
(1) 对已知的信号进行截短(如果本来就是有限长的则不用);
(2) 对截短的离散信号做N点DFT(这里的N应该大于离散信号的点数,N越大,在频域的采样就越密集);
(3) 将横坐标转换为【-pi,pi】,符合实际的情况(/N*2*pi)。
具体的解释见下面的代码(具体代码粘贴在最后面)。
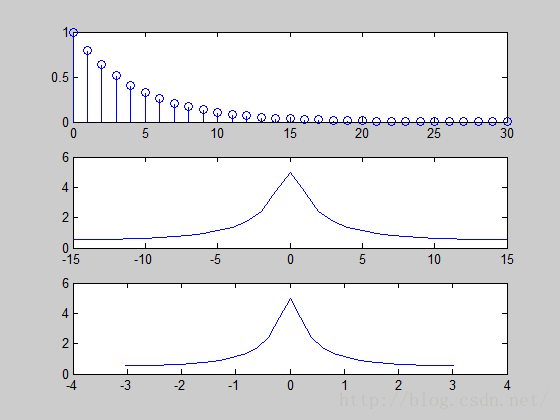
下面是一个例子:
运行结果如下:
(二) 用DFT分析离散周期信号的频谱(离散周期信号的DTFS为离散周期的,以基波周期N为周期)
比较DTFS和DFT公式,可以发现:
如上面提到的,上面的DTFS公式与实际的相差了N倍,所以在画频谱的时候需要考虑进去。
离散周期信号的基波周期为N,取其中N点做N点DFT相当于离散周期信号DTFS的一个N周期内的值。
所以,分析离散周期信号的频谱的思路如下:
(1) 确定基波周期N;
(2) 取离散周期信号的N个点,如【0,N-1】;
(3) 做N点DFT(幅度上要除以N,原因在DTFS公式比DFT公式前面多了一项1/N);
(4) 得到离散周期信号在一个基波周期内的傅里叶系数;
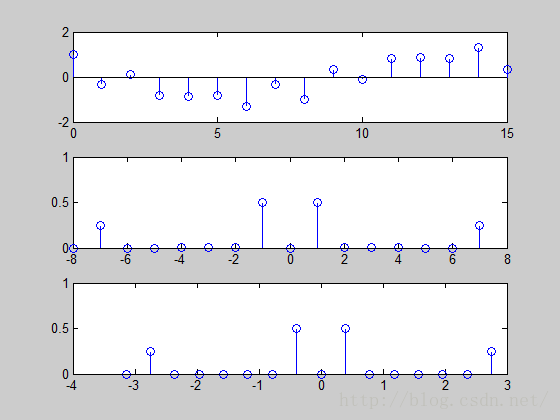
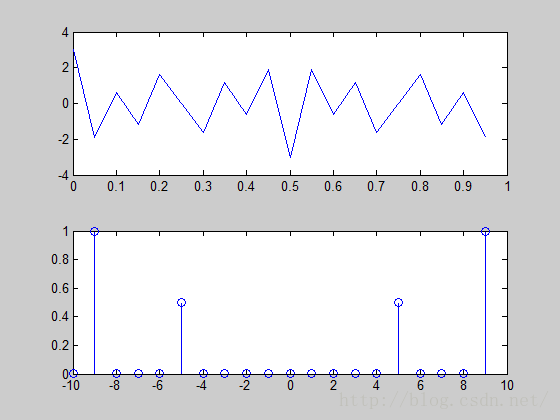
下面是一个例子:
(三) 用DFT分析连续非周期信号的频谱(连续非周期信号的CTFT为连续非周期的)
利用采样,将连续非周期信号,转换成离散非周期信号,对得到的离散非周期信号做DFT,类似于(一),最后再利用模拟频率与数字频率的关系(模拟频率乘以采样周期等于数字频率)将横坐标由数字频率转换为模拟频率:
分析连续非周期信号的频谱的思路如下:
(1) 根据需要截短(如果连续信号是无限长的);
(2) 估计信号的最高频率fm;
(3) 采样频率fs>2*fm;
(4) 按T(T=1/fs)对连续信号进行采样;
(5) 对采样后的信号(相当于离散非周期信号)做N点DFT(此处的N应该大于等于采样点数,而且越大越好,越大代表如(一)分析的,在频域上的采样就越密集,对离散非周期信号的频谱更好地逼近),DFT结果幅度上要除以T,这是采样导致的结果;
(6) 将横坐标转换成模拟频率(/N*2*pi*fs)。
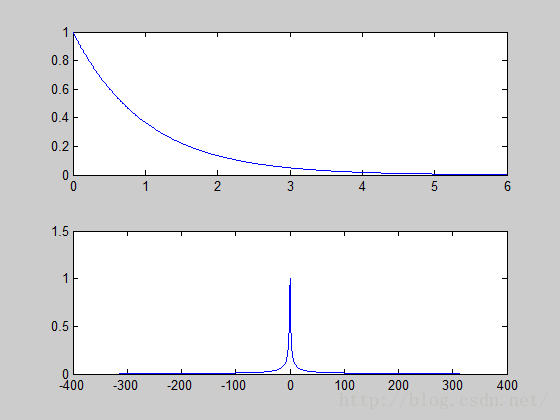
下面是一个例子:
(四) 用DFT分析连续周期信号的频谱(连续周期信号的CTFS为离散非周期)
对连续周期信号在一个或多个基波周期长度内进行采样,采样频率fs>2*fm,对采样点做等长(假设为N)的DFT(幅度上得除以N,原因同(二)),由于用了采样,所以同(三)一样需要将数字频率转换成模拟频率(/N*2*pi*fs)。
分析连续周期信号的频谱的思路如下:
(1) 确定基波周期To和最高频率fm,采样频率fs>2*fm;
(2) 对连续周期信号的一个周期(可以多个周期)以频率fs进行均匀采样,采样点数为N;
(3) 对采样点做N点DFT(幅度/N,原因同(二));
(4) 将横坐标转换成模拟频率(/N*2*pi*fs)。
下面是一个例子:
全部代码:
function test1
%%%%%%%%(1)离散非周期%%%%%%%%%%%%% x = 0.8.^n;(频谱为连续周期(周期为2*pi))
N = 31;%%%%%无限长的信号应根据需要先截断
n = 0:N-1;
x = 0.8.^n;
X = fft(x,N);%%%%%%对截断的离散信号做N点DFT相当于在其频谱的【0,2pi】区间做N点均匀采样
figure;
subplot(3,1,1);
stem(n,x);
subplot(3,1,2);
plot([-(N-1)/2:(N-1)/2],abs(fftshift(X)));%%%%%%此处画出来的频谱图的横坐标是对离散非周期信号的实际频谱在[-pi,pi]区间采样的点
subplot(3,1,3);
plot([-(N-1)/2:(N-1)/2]./N*2*pi,abs(fftshift(X)));%%%%%%此处将频谱的横坐标转化为[-pi,pi]区间,这才是实际情况(离散非周期信号的DTFT是连续周期的,以2pi为周期)
%%%%%%(2)离散周期%%%%%%%%%%%%% x =cos(pi/8*n+pi/3)+0.5cos(7*pi*n/8);(频谱为离散周期(周期为基波周期N))
%%%%%%%%确定信号的基波周期为16
N = 16;
n = 0:N-1;
x = cos(pi/8*n+pi/3)+0.5*cos(7*pi*n/8);
X = fft(x,N)/N;%%%%%%对截断的离散信号做N点DFT,得出的结果相当于是原周期信号在【0,N-1】的傅里叶系数,除以N表示DFT公式与离散周期信号傅立叶级数公式的关系所需;
figure;
subplot(3,1,1);
stem(n,x);
subplot(3,1,2);
stem([-N/2:N/2-1],abs(fftshift(X)));%%%%%%此处画出来的频谱图的横坐标是离散周期信号的CTFS(傅里叶系数,以N为周期),在[-N/2:N/2-1]的变化,即谐波次数(基波周期N=16的情况下)
subplot(3,1,3);
stem([-N/2:N/2-1]./N*2*pi,abs(fftshift(X)));%%%%%%此处画出来的频谱图的横坐标是将上面的谐波次数乘上基波频率2*pi/N
%%%%%%(3)连续非周期%%%%%%%%%%%%% x = exp(-1*t);(频谱为连续非周期)
%%%%%%取x的最高频率fm为25,根据奈奎斯准则,采样率取100>2*25
%%%%%此处的信号无限长,同样需要进行截短,这里去前6秒
fs = 100;
Tp = 6;
T = 1/fs;
t = 0:T:Tp;
x = exp(-1*t);
N = 1024;%%%%%%%进行DFT的点数,这里的N只要比采样点数多即可,越大越能够逼近
X = fft(x,N)*T;%%%%%%此处乘上T是由于对连续信号采样导致的频谱幅度变化。
subplot(2,1,1);
plot(t,x);
subplot(2,1,2);
%%%%%%此处画出来的频谱图的横坐标是[-N/2:N/2-1]*(2*pi/N)是对采样得到的离散非周期信号做频谱分析得到的数字角频率,乘上fs即除以采样周期T才得到模拟角频率
plot([-N/2:N/2-1]*(2*pi/N)*fs,abs(fftshift(X)));
%%%%%%%(4)连续周期%%%%%%%%%%%%% x =cos(10*pi*t)+2*cos(18*pi*t);(频谱为离散非周期)
%%%%%%%因为x的基波频率为2*pi,基波周期Tp为1s,最高次谐波为9,即最高频率为9Hz
%%%%%%%由奈奎斯采样准则确定出采样频率fs=20>2*9
fs = 20;
T = 1/fs;
Tp = 1;
N = Tp/T;
t = 0:T:Tp-T;
x = cos(10*pi*t)+2*cos(18*pi*t);
X = fft(x,N)/N;
subplot(2,1,1);
plot(t,x);
subplot(2,1,2);
stem([-N/2:N/2-1]/N*fs,abs(fftshift(X)));%%%%%%此处画出来的频谱图的横坐标是[-N/2:N/2-1]*(2*pi/N)是对采样得到的离散非周期信号做频谱分析得到的数字角频率,乘上fs即除以采样周期T才得到模拟角频率