模拟幅度调制相干解调系统抗噪声性能仿真分析
文章目录
- 1.引言
- 2.系统模型
- 2.1 模拟调制系统的基本系统模型
- 2.2 常规调幅(AM)
- 2.3 抑制载波双边带调幅(DSB-SC)
- 2.4 单边带调幅(SSB)
- 3.抗噪声性能理论分析
- 3.1 常规调幅(AM)
- 3.2 抑制载波双边带调幅(DSB-SC)
- 3.3 单边带调幅(SSB)
- 4.仿真实现与仿真结果
- 4.1 AM调制解调
- 4.1.1 系统仿真参数设置
- 4.1.2 生成基带信号与载波信号
- 4.1.3 产生噪声及通过系统
- 4.1.4 AM相干解调
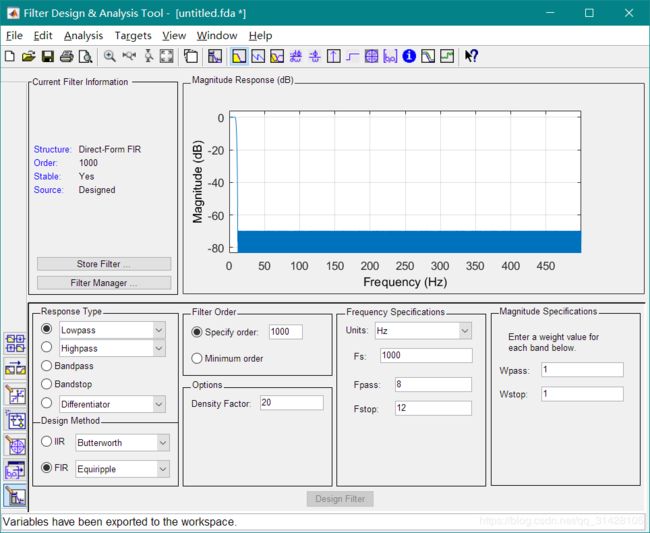
- 4.1.5 滤波器设置
- 4.2 DSB-SC调制解调
- 4.2.1 系统仿真参数设置
- 4.2.2 生成DSB-SC调制信号
- 4.2.3 DSB-SC相干解调
- 4.3 SSB调制解调
- 4.3.1 系统仿真参数设置
- 4.3.2 SSB调制与解调
- 5.小结
- 6.参考文献
1.引言
模拟调制技术在20世纪中曾有较大的应用,如军事通信、短波通信、模拟移动通信、模拟调频广播和模拟调幅广播等。虽然现在通信的发展趋势为数字化,但数字技术并不能完全替代模拟技术,而且模拟调制技术是通信理论的基本知识。模拟信号的载波调制电路里面经常要用到调制与解调,其中幅度调制就是用信号控制载波的幅度,使载波幅度岁调制信号而变化,主要包括模拟常规调幅(AM)、抑制载波双边带调幅(DSB-SC)、单边带调幅(SSB)。而在模拟信号的传输过程中,噪声的干扰总是不可避免的,因此我们在这里对模拟幅度调制相干解调系统抗噪声性能进行分析。分析的工具为MATLAB2016。
2.系统模型
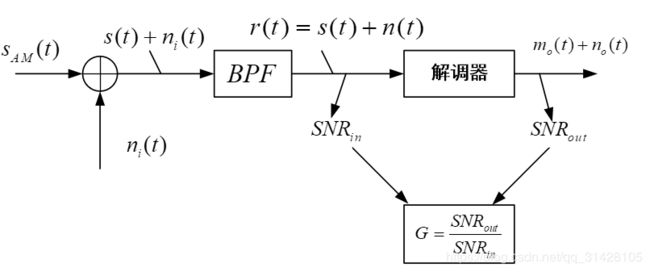
2.1 模拟调制系统的基本系统模型
在上图中, m ( t ) m(t) m(t)是带宽为 W W W、功率为 P m P_m Pm的模拟基带信号。 s ( t ) s(t) s(t)是带宽为 B B B、功率为 P R P_R PR的已调信号。本次实验考虑的已调信号包括 A M AM AM、 D S B − S C DSB-SC DSB−SC、 S S B SSB SSB。
设要传输的基带信号为 m ( t ) = c o s 2 π f m t − − − ( 2.1.1 ) m(t)=cos2\pi f_mt---(2.1.1) m(t)=cos2πfmt−−−(2.1.1)
其傅氏变换为 M ( f ) = 1 2 [ δ ( f − f m ) + δ ( f + f m ) ] − − − ( 2.1.2 ) M(f)= \frac{1}{2}[\delta(f-f_m)+\delta(f+f_m)]---(2.1.2) M(f)=21[δ(f−fm)+δ(f+fm)]−−−(2.1.2)
载波信号 c ( t ) c(t) c(t): c ( t ) = A c c o s 2 π f c t − − − ( 2.1.3 ) c(t)=A_ccos2\pi f_ct---(2.1.3) c(t)=Accos2πfct−−−(2.1.3)
A c A_c Ac为载波幅度, f c f_c fc为载波频率。 c ( t ) c(t) c(t)的傅氏变换为 C ( f ) = A c 2 [ δ ( f − f c ) + δ ( f + f c ) ] − − − ( 2.1.4 ) C(f)= \frac{A_c}{2}[\delta(f-f_c)+\delta(f+f_c)]---(2.1.4) C(f)=2Ac[δ(f−fc)+δ(f+fc)]−−−(2.1.4)
又由以上系统框图, m ( t ) m(t) m(t)经过调制器后得到已调信号 s ( t ) s(t) s(t),在这里先考虑无噪声传输的情况。
已知相干解调的原理是将调制的信号先乘以一个与高频载波信号 c ( t ) c(t) c(t)同频同相的接收机端载波信号 c ′ ( t ) c^{\prime}(t) c′(t): c ′ ( t ) = c o s 2 π f c t − − − ( 2.1.5 ) c^{\prime}(t)=cos2\pi f_ct---(2.1.5) c′(t)=cos2πfct−−−(2.1.5)
则经过相干解调的信号 s d ( t ) s_d(t) sd(t): s d ( t ) = m ( t ) c ′ ( t ) − − − ( 2.1.6 ) s_d(t)=m(t)c^{\prime}(t)---(2.1.6) sd(t)=m(t)c′(t)−−−(2.1.6)
最后将 s d ( t ) s_d(t) sd(t)经过一个低通滤波器LPF,即可得到解调信号
2.2 常规调幅(AM)
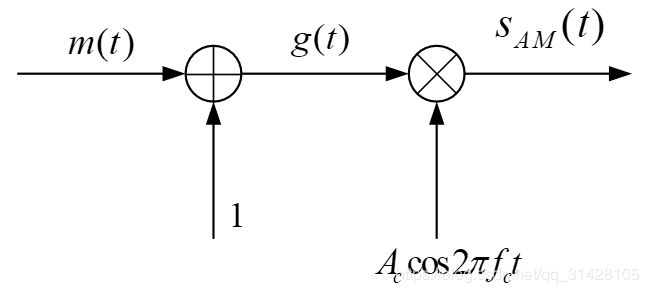
在AM调制中,幅度已调信号 s A M ( t ) s_{AM}(t) sAM(t)的时域表达式为: s A M ( t ) = A c [ 1 + a m ( t ) ] c o s 2 π f c t − − − ( 2.2.1 ) s_{AM}(t)=A_c[1+am(t)]cos2\pi f_ct---(2.2.1) sAM(t)=Ac[1+am(t)]cos2πfct−−−(2.2.1)
标量因子 a > 0 a>0 a>0称为调制指数或调幅系数。为了在解调时使用包络检波而不是真的恢复出原基带信号 m ( t ) m(t) m(t),要求 a ≤ 1 a\le 1 a≤1。
若 m ( t ) m(t) m(t)的频谱为 M ( f ) M(f) M(f),则 s A M ( t ) s_{AM}(t) sAM(t)的傅氏变换为: S A M ( f ) = A c 2 [ δ ( f − f c ) + M ( f − f c ) + δ ( f + f c ) + M ( f + f c ) ] − − − ( 2.2.2 ) S_{AM}(f)=\frac {A_c}{2}[\delta(f-f_c)+M(f-f_c)+\delta(f+f_c)+M(f+f_c)]---(2.2.2) SAM(f)=2Ac[δ(f−fc)+M(f−fc)+δ(f+fc)+M(f+fc)]−−−(2.2.2)

在AM相干解调系统模型中,带通滤波器BPF的带宽 B A M = 2 B B_{AM}=2B BAM=2B( B B B为 m ( t ) m(t) m(t)的带宽)。
而 s d ( t ) = s A M ( t ) c ′ ( t ) s_d(t)=s_{AM}(t)c^{\prime}(t) sd(t)=sAM(t)c′(t),即 s d ( t ) = A c 2 [ 1 + m ( t ) ] [ 1 + c o s 4 π f c t ] − − − ( 2.2.3 ) s_d(t)=\frac{A_c}{2}[1+m(t)][1+cos4\pi f_ct]---(2.2.3) sd(t)=2Ac[1+m(t)][1+cos4πfct]−−−(2.2.3)
其傅氏变换 S d ( f ) S_d(f) Sd(f): S d ( f ) = A c 2 M ( f ) + A c 4 [ M ( f − 2 f c ) + M ( f + 2 f c ) ] + A c 2 δ ( f ) + A c 4 [ δ ( f − 2 f c ) + δ ( f + 2 f c ) ] − − − ( 2.2.4 ) S_d(f)=\frac{A_c}{2}M(f)+\frac{A_c}{4}[M(f-2f_c)+M(f+2f_c)]+\frac{A_c}{2}\delta(f)+\frac{A_c}{4}[\delta(f-2f_c)+\delta(f+2f_c)]---(2.2.4) Sd(f)=2AcM(f)+4Ac[M(f−2fc)+M(f+2fc)]+2Acδ(f)+4Ac[δ(f−2fc)+δ(f+2fc)]−−−(2.2.4)
2.3 抑制载波双边带调幅(DSB-SC)
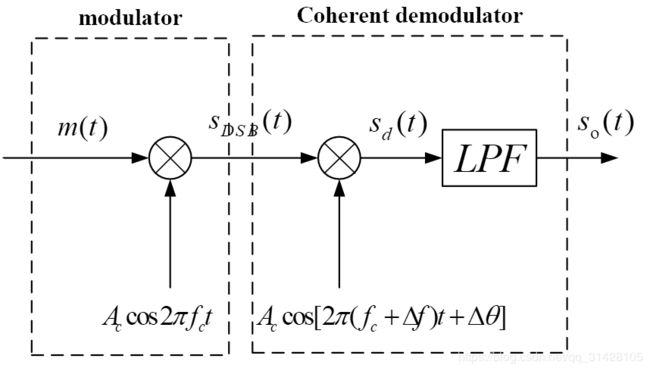
双边带调制,在幅度调制中,载波分量并不携带信息,将AM调制中的直流分类去掉,即为双边带调制。DSB-SC信号的时域表达式 s D S B ( t ) s_{DSB}(t) sDSB(t): s D S B ( t ) = A c m ( t ) c o s 2 π f c t − − − ( 2.3.1 ) s_{DSB}(t)=A_cm(t)cos2\pi f_ct---(2.3.1) sDSB(t)=Acm(t)cos2πfct−−−(2.3.1)
其傅氏变换为 S D S B ( f ) = A c 2 [ M ( f − f c ) + M ( f + f c ) ] − − − ( 2.3.2 ) S_{DSB}(f)=\frac{A_c}{2}[M(f-f_c)+M(f+f_c)]---(2.3.2) SDSB(f)=2Ac[M(f−fc)+M(f+fc)]−−−(2.3.2)
s D S B ( t ) s_{DSB}(t) sDSB(t)与恢复载波 A c c o s [ 2 π ( f c + Δ f ) t + Δ θ ] A_ccos[2\pi (f_c+\Delta f)t+\Delta \theta] Accos[2π(fc+Δf)t+Δθ]相乘的结果是: s d ( t ) = A c 2 2 m ( t ) { c o s ( 2 π Δ f t + Δ θ ) + c o s [ 2 π ( 2 f c + Δ f ) + Δ θ ] } − − − ( 2.3.3 ) s_d(t)=\frac{A_c^2}{2}m(t)\lbrace {cos(2\pi \Delta ft+\Delta \theta) +cos[2\pi (2f_c+\Delta f)+\Delta \theta ]} \rbrace---(2.3.3) sd(t)=2Ac2m(t){cos(2πΔft+Δθ)+cos[2π(2fc+Δf)+Δθ]}−−−(2.3.3)
经过低通滤波器LPF后,剩余已解调有效信号 s o ( t ) s_o(t) so(t): s o ( t ) = A c 2 2 m ( t ) c o s ( 2 π Δ f t + Δ θ ) − − − ( 2.3.4 ) s_o(t)=\frac{A_c^2}{2}m(t)cos(2\pi \Delta ft+\Delta \theta)---(2.3.4) so(t)=2Ac2m(t)cos(2πΔft+Δθ)−−−(2.3.4)
2.4 单边带调幅(SSB)
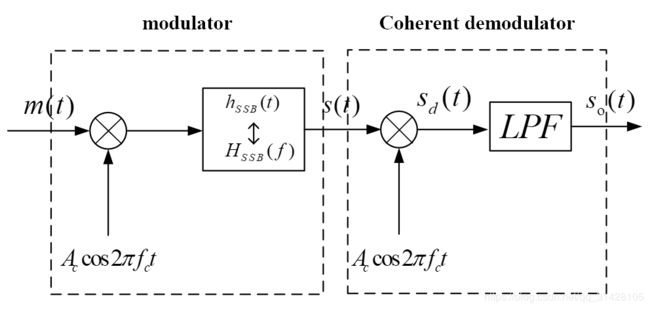
单边带调幅信号是只取DSB_SC信号中的上边带或下边带分量所得到的信号。产生SSB信号的一种基本方法为滤波法如图2.4.1modulator所示, H S S B ( f ) H_{SSB}(f) HSSB(f)为单边带滤波器的传递函数。分为下边带滤波器 H L S S B ( f ) H_{LSSB}(f) HLSSB(f)和上边带滤波器 H U S S B ( f ) H_{USSB}(f) HUSSB(f)。下边带滤波器为
H L S S B ( f ) = { 1 , ∣ f ∣ < f c 0 , ∣ f ∣ ≥ f c − − − ( 2.4.1 ) H_{LSSB}(f)= \begin{cases} 1,&|f|< f_c \\ 0,&|f|\ge f_c \end{cases}---(2.4.1) HLSSB(f)={1,0,∣f∣<fc∣f∣≥fc−−−(2.4.1)
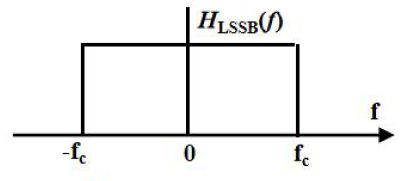
H L S S B ( f ) = 1 2 [ s g n ( f + f c ) − s g n ( f − f c ) ] − − − ( 2.4.2 ) H_{LSSB}(f)=\frac{1}{2}[sgn(f+f_c)-sgn(f-f_c)]---(2.4.2) HLSSB(f)=21[sgn(f+fc)−sgn(f−fc)]−−−(2.4.2)
上边带滤波器为
H U S S B ( f ) = { 1 , ∣ f ∣ > f c 0 , ∣ f ∣ ≤ f c − − − ( 2.4.3 ) H_{USSB}(f)= \begin{cases} 1,&|f|> f_c \\ 0,&|f|\le f_c \end{cases}---(2.4.3) HUSSB(f)={1,0,∣f∣>fc∣f∣≤fc−−−(2.4.3)
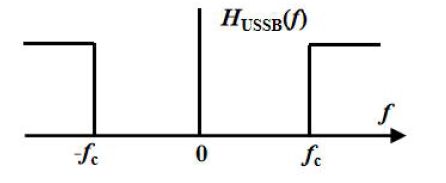
H U S S B ( f ) = 1 − H L S S B ( f ) − − − ( 2.4.4 ) H_{USSB}(f)=1-H_{LSSB}(f)---(2.4.4) HUSSB(f)=1−HLSSB(f)−−−(2.4.4)
经过单边带滤波器后 S S S B ( f ) S_{SSB}(f) SSSB(f)可表示为: S S S B ( f ) = 1 2 [ M ( f − f c ) + M ( f + f c ) ] H S S B ( f ) − − − ( 2.4.5 ) S_{SSB}(f)=\frac{1}{2}[M(f-f_c)+M(f+f_c)]H_{SSB}(f)---(2.4.5) SSSB(f)=21[M(f−fc)+M(f+fc)]HSSB(f)−−−(2.4.5)
下面分析单边带信号解调系统,可知其原理与DCB-SC相似。
3.抗噪声性能理论分析
3.1 常规调幅(AM)
由之前对系统模型的分析得式2.2.3和2.2.4,而通过带通滤波器的白噪声信号 n ( t ) n(t) n(t): n ( t ) = n c ( t ) c o s 2 π f c t − n s s i n 2 π f c t − − − ( 3.1.1 ) n(t)=n_c(t)cos2\pi f_ct-n_ssin2\pi f_ct---(3.1.1) n(t)=nc(t)cos2πfct−nssin2πfct−−−(3.1.1)
通过乘法器后: n d ( t ) = n c ( t ) c o s 2 2 π f c t − n s ( t ) s i n 2 π f c t c o s 2 π f c t t = 1 2 n c ( t ) + 1 2 n c ( t ) c o s 4 π f c t − 1 2 n s ( t ) s i n 4 π f c t − − − ( 3.1.2 ) n_d(t)=n_c(t)cos^2 2\pi f_ct-n_s(t)sin2\pi f_ctcos2\pi f_ctt=\frac{1}{2}n_c(t)+\frac{1}{2}n_c(t)cos4\pi f_ct-\frac{1}{2}n_s(t)sin4\pi f_ct---(3.1.2) nd(t)=nc(t)cos22πfct−ns(t)sin2πfctcos2πfctt=21nc(t)+21nc(t)cos4πfct−21ns(t)sin4πfct−−−(3.1.2)
输出噪声 n o ( t ) = 1 2 n c ( t ) − − − ( 3.1.3 ) n_o(t)=\frac{1}{2}n_c(t)---(3.1.3) no(t)=21nc(t)−−−(3.1.3)
输出端信号: m A M o ( t ) = A c 2 m ( t ) − − − ( 3.1.4 ) m_{AMo}(t)=\frac{A_c}{2}m(t)---(3.1.4) mAMo(t)=2Acm(t)−−−(3.1.4) n o ( t ) = 1 2 n c ( t ) − − − ( 3.1.5 ) n_o(t)=\frac{1}{2}n_c(t)---(3.1.5) no(t)=21nc(t)−−−(3.1.5)
则输入信噪比为: S N R i n = P S a m P N = A c 2 2 [ 1 + P m ] 2 n 0 B − − − ( 3.1.6 ) SNR_{in}=\frac{P_{Sam}}{P_N}=\frac {\frac {A_c^2}{2}[1+P_m]}{2n_0B}---(3.1.6) SNRin=PNPSam=2n0B2Ac2[1+Pm]−−−(3.1.6)
输出信噪比为: S N R o u t = P S o P N o = A c 2 P m 2 n 0 B − − − ( 3.1.7 ) SNR_{out}=\frac {P_{So}}{P_{No}}=\frac {A_c^2P_m}{2n_0B}---(3.1.7) SNRout=PNoPSo=2n0BAc2Pm−−−(3.1.7)
可得 G A M = S N R o u t S N R i n = 2 P m 1 + P m − − − ( 3.1.8 ) G_{AM}=\frac {SNR_{out}}{SNR_{in}}=\frac {2P_m}{1+P_m}---(3.1.8) GAM=SNRinSNRout=1+Pm2Pm−−−(3.1.8)
3.2 抑制载波双边带调幅(DSB-SC)
根据2.3对DSB-SC系统模型的分析,再对噪声进行分析 n ( t ) = n c ( t ) c o s 2 π f c t − n s s i n 2 π f c t − − − ( 3.2.1 ) n(t)=n_c(t)cos2\pi f_ct-n_ssin2\pi f_ct---(3.2.1) n(t)=nc(t)cos2πfct−nssin2πfct−−−(3.2.1)与式3.1.1相同,可见两个解调系统的带通滤波器BPF带宽 B D S B = 2 B B_{DSB}=2B BDSB=2B( B B B为 m ( t ) m(t) m(t)的带宽),对噪声起到相同的作用。 n d ( t ) n_d(t) nd(t)和 n o ( t ) n_o(t) no(t)与式3.1.2和3.1.3相同。
∴ \therefore ∴ S N R i n = P D S B i n P N = A c 2 P m 2 2 n 0 B − − − ( 3.2.2 ) SNR_{in}=\frac {P_{DSBin}}{P_N}=\frac{\frac {A_c^2P_m}{2}}{2n_0B}---(3.2.2) SNRin=PNPDSBin=2n0B2Ac2Pm−−−(3.2.2)
S N R o u t = P D S B o u t P N o = A c 2 P m 4 2 n 0 B − − − ( 3.2.3 ) SNR_{out}=\frac {P_{DSBout}}{P_{No}}=\frac{\frac {A_c^2P_m}{4}}{2n_0B}---(3.2.3) SNRout=PNoPDSBout=2n0B4Ac2Pm−−−(3.2.3)
∴ \therefore ∴ G D S B − S C = S N R o u t S N R i n = 2 − − − ( 3.2.4 ) G_{DSB-SC}=\frac {SNR_{out}}{SNR_{in}}=2---(3.2.4) GDSB−SC=SNRinSNRout=2−−−(3.2.4)
3.3 单边带调幅(SSB)
对噪声的分析与3.1和3.2相同,结果也相同。直接分析输入输出信噪比。
S N R i n = P S S B i n P N = A c 2 P m 4 n 0 B − − − ( 3.3.1 ) SNR_{in}=\frac {P_{SSBin}}{P_N}=\frac{\frac {A_c^2P_m}{4}}{n_0B}---(3.3.1) SNRin=PNPSSBin=n0B4Ac2Pm−−−(3.3.1)
S N R o u t = P S S B o u t P N o = 1 4 A c 2 P m 4 1 4 n 0 B = S N R i n − − − ( 3.3.2 ) SNR_{out}=\frac {P_{SSBout}}{P_{No}}=\frac{\frac{1}{4}\frac {A_c^2P_m}{4}}{\frac{1}{4}n_0B}=SNR_{in}---(3.3.2) SNRout=PNoPSSBout=41n0B414Ac2Pm=SNRin−−−(3.3.2)
∴ \therefore ∴ G S S B = S N R o u t S N R i n = 1 − − − ( 3.3.3 ) G_{SSB}=\frac {SNR_{out}}{SNR_{in}}=1---(3.3.3) GSSB=SNRinSNRout=1−−−(3.3.3)
4.仿真实现与仿真结果
4.1 AM调制解调
4.1.1 系统仿真参数设置
T_stop=0.5;%截止时间
T=T_stop-T_start;%仿真持续时间
T_sample=1/1000;%采样间隔
f_sample=1/T_sample; % 采样速率
N_sample=T/T_sample;% 采样点数
fm=10;%调制信号频率
fc=100;%载波频率
n=0:N_sample;
4.1.2 生成基带信号与载波信号
mt=cos(2*pi*fm*n*T_sample);
ct=cos(2*pi*fc*n*T_sample);
则AM调制信号 s ( t ) s(t) s(t)为:
st=(1+mt).*ct;
对信号做傅氏变换,观察其时域波形与频谱
f_res=f_sample/length(st);%频率分辨率
f_max=f_res*length(st)/2;%最大频率
F=abs(fft(st));
F_rearrange=[F(length(st)/2+1:length(st)-1),F(1:length(st)/2)];
4.1.3 产生噪声及通过系统
noise_i=wgn(1,length(st),-33);
noise=conv(noise_i,Bandpass);
PSD_Noise_i=abs(fft(noise)).^2*T_sample/T/f_sample;
figure(2);
f_res=f_sample/length(noise);%频率分辨率
f_max=f_res*length(noise)/2;%最大频率
F1_rearrange=[PSD_Noise_i(length(noise)/2+1:length(noise)-1),PSD_Noise_i(1:length(noise)/2)];
plot((-length(noise)/2+2:length(noise)/2-2)*f_res,F1_rearrange(1:length(noise)-3));
title('PSD-Noise-i');
P_noise_i=sum(PSD_Noise_i)/length(PSD_Noise_i)*f_sample;
P_in=P_st/P_noise_i;
4.1.4 AM相干解调
sdt=st.*ct;
c1t=conv(ct,Bandpass);
ndt=noise.*c1t;
sot=conv(sdt,Lowpass);
not=conv(ndt,Lowpass);
figure(3);
f_res=f_sample/length(sot);%频率分辨率
F=abs(fft(sot));
F_rearrange=[F(length(sot)/2+1:length(sot)-1),F(1:length(sot)/2)];
subplot(2,1,1);
plot((-length(sot)/2+1:length(sot)/2-1)*f_res,F_rearrange(1:length(sot)-1));
title('So(f)');
PSD_sot=abs(fft(sot)).^2*T_sample/T/f_sample;
P_sot=sum(PSD_sot)/length(PSD_sot)*f_sample;
f_res=f_sample/length(not);%频率分辨率
PSD_Noise_o=abs(fft(not)).^2*T_sample/T/f_sample;
F1_rearrange=[PSD_Noise_o(length(not)/2+1:length(not)-1),PSD_Noise_o(1:length(not)/2)];
subplot(2,1,2);
plot((-length(not)/2+2:length(not)/2-2)*f_res,F1_rearrange(1:length(not)-3));
title('PSD-Noise-o');
P_not=sum(PSD_Noise_o)/length(PSD_Noise_o)*f_sample;
P_out=P_sot/P_not;
4.1.5 滤波器设置
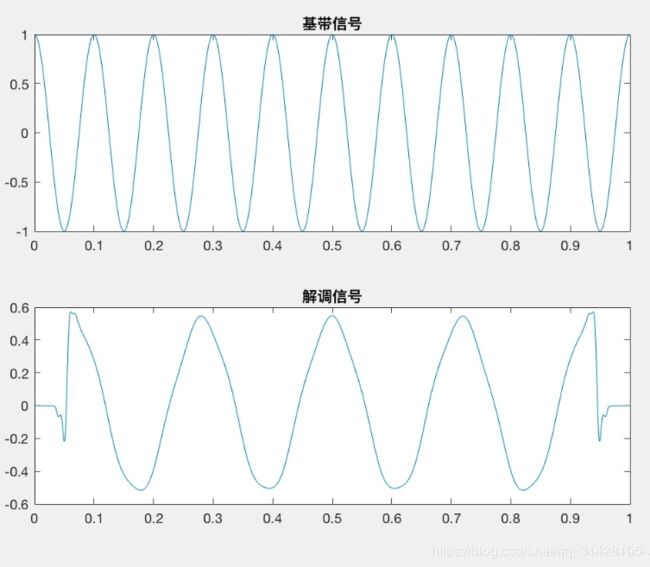
分析:
调制过程即为频谱搬移的过程,且未产生新的频率分量,而相干解调后得出的波形与频谱都与原基带信号有一定的差异,时域波形为有限的信号,在一定的时间内解调出来的信号与基带信号误差较小,而在时限外则误差较大,时域波形趋于平稳直至消失,从而导致其频域波形有较大的误差。
4.2 DSB-SC调制解调
4.2.1 系统仿真参数设置
T_stop=0.5;%截止时间
T=T_stop-T_start;%仿真持续时间
T_sample=1/1000;%采样间隔
f_sample=1/T_sample; % 采样速率
N_sample=T/T_sample;% 采样点数
fm=10;%调制信号频率
fc=100;%载波频率
n=0:N_sample;
4.2.2 生成DSB-SC调制信号
m=cos(2*pi*fm*n*T_sample);
dsb=m.*cos(2*pi*fc*n*T_sample);
f_res=f_sample/N_sample;%频率分辨率
f_max=f_res*N_sample/2;%最大频率
F=abs(fft(m));
F_rearrange=[F(N_sample/2+1:N_sample-1),F(1:N_sample/2)];
F=abs(fft(dsb));
F_rearrange=[F(N_sample/2+1:N_sample-1),F(1:N_sample/2)];
4.2.3 DSB-SC相干解调
%解调
nn=0:5633;
mm=2*dsb.*cos(2*pi*100*n*T_sample);
mm=conv(mm,DSBNum);
F=abs(fft(m));
F_rearrange=[F(N_sample/2+1:N_sample-1),F(1:N_sample/2)];
F=abs(fft(mm));
F_rearrange=[F(N_sample/2+1:N_sample-1),F(1:N_sample/2)];
分析:
与AM系统相类似,调制过程即为频谱搬移的过程,且未产生新的频率分量,而相干解调后得出的波形与频谱都与原基带信号有一定的差异,而频谱图则误差较大只包含了一半的冲击信号。这是因为仿真所用滤波器只有正频率,所以只有一半,导致失真。
4.3 SSB调制解调
4.3.1 系统仿真参数设置
T_stop=0.5;%截止时间
T=T_stop-T_start;%仿真持续时间
T_sample=1/1000;%采样间隔
f_sample=1/T_sample; % 采样速率
N_sample=T/T_sample;% 采样点数
fm=10;%调制信号频率
fc=100;%载波频率
n=0:N_sample;
4.3.2 SSB调制与解调
mt=cos(2*pi*10*n*T_sample);
ct=cos(2*pi*100*n*T_sample);
s1t=mt.*ct;
st=conv(s1t,Lowpass1);
figure(1);
subplot(2,1,1);
n1=0:length(st)-1;
plot(n1*T_sample,st);
title('s(t)时域波形');
f_res=f_sample/length(st);%频率分辨率
f_max=f_res*length(st)/2;%最大频率
F=abs(fft(st));
F_rearrange=[F(length(st)/2+1:length(st)-1),F(1:length(st)/2)];
subplot(2,1,2);
plot((-length(st)/2+2:length(st)/2-2)*f_res,F_rearrange(1:length(st)-3));
title('s(t)频域波形');
PSD_st=abs(fft(st)).^2*T_sample/T/f_sample;
P_st=sum(PSD_st)/length(PSD_st)*f_sample;
%%noise的创建
noise_i=wgn(1,length(st),-33);
noise=conv(noise_i,Bandpass);
PSD_Noise_i=abs(fft(noise)).^2*T_sample/T/f_sample;
figure(2);
f_res=f_sample/length(noise);%频率分辨率
f_max=f_res*length(noise)/2;%最大频率
F1_rearrange=[PSD_Noise_i(length(noise)/2+1:length(noise)-1),PSD_Noise_i(1:length(noise)/2)];
plot((-length(noise)/2+2:length(noise)/2-2)*f_res,F1_rearrange(1:length(noise)-3));
title('PSD-Noise-i');
P_noise_i=sum(PSD_Noise_i)/length(PSD_Noise_i)*f_sample;
P_in=P_st/P_noise_i;
%%解调
c1t=cos(2*pi*100*n1*T_sample);
sdt=st.*c1t;
c2t=conv(c1t,Bandpass);
ndt=noise.*c2t;
sot=conv(sdt,Lowpass);
not=conv(ndt,Lowpass);
figure(3);
f_res=f_sample/length(sot);%频率分辨率
F=abs(fft(sot));
F_rearrange=[F(length(sot)/2+1:length(sot)-1),F(1:length(sot)/2)];
subplot(2,1,1);
plot((-length(sot)/2+2:length(sot)/2-2)*f_res,F_rearrange(1:length(sot)-3));
title('So(t)');
PSD_sot=abs(fft(sot)).^2*T_sample/T/f_sample;
P_sot=sum(PSD_sot)/length(PSD_sot)*f_sample;
f_res=f_sample/length(not);%频率分辨率
PSD_Noise_o=abs(fft(not)).^2*T_sample/T/f_sample;
F1_rearrange=[PSD_Noise_o(length(not)/2+1:length(not)-1),PSD_Noise_o(1:length(not)/2)];
subplot(2,1,2);
plot((-length(not)/2+2:length(not)/2-2)*f_res,F1_rearrange(1:length(not)-3));
title('PSD-Noise-o');
P_not=sum(PSD_Noise_o)/length(PSD_Noise_o)*f_sample;
P_out=P_sot/P_not;
%%输出输入功率比值
G=P_out/P_in;
分析:
由仿真结果易得,SSB调制与解调与DSB基本一模一样,只是差了一个边带的问题,不过也正是由于这个问题就导致二者的增益比恰好是。SSB系统的误差较前两个系统的都大,时域波形存在较大的失真,得出的解调波形角频率与幅度都与基带信号不符,解调信号的频谱也出现了偏移与缺失,并且分析结果,可初步认为是在产生与解调SSB信号时运用了多次滤波器而导致的。
5.小结
通过本次的仿真实验可以得出在AM、DSB-SC、SSB这三个系统中DSB-SC的解调增益最大且为定值2,而SSB系统的解调增益也为定值1,可见,DSB-SC系统的抗干扰能力较SSB系统更强,而AM相干解调系统的解调增益不为定值,且其大小随着基带信号功率的变化而变化但小于2,即DSB-SC系统的抗干扰能力最强,AM系统的抗干扰能力与基带信号的功率相关,且功率越大抗干扰能力越强,SSB系统的抗干扰能力为DSB-SC系统的一半。
6.参考文献
周烔槃.通信原理.北京:北京邮电大学出版社,2015