(AtCoder - 1974)いろはちゃんとマス目 / Iroha and a Grid(乘法逆元+组合计数)

前言

一道花了很长时间搞懂的题

题目

We have a large square grid with H rows and W columns. Iroha is now standing in the top-left cell. She will repeat going right or down to the adjacent cell, until she reaches the bottom-right cell.
However, she cannot enter the cells in the intersection of the bottom A rows and the leftmost B columns. (That is, there are A×B forbidden cells.) There is no restriction on entering the other cells.
Find the number of ways she can travel to the bottom-right cell.
Since this number can be extremely large, print the number modulo 10^9+7.

题目链接

题目链接

题目大意

给你一个矩形,高H,宽W，然后在它的左下角有一个高为a,宽为b的子矩形,现在有一个人想走最短距离从左上角(1,1)走到右下角(H,W)且不经过左下角的矩形,求总方案数，由于答案可能很大,答案要模(10^9+7)。

数据范围

1≦H,W≦100,000 1 ≦ H , W ≦ 100 , 000
1≦A<H 1 ≦ A < H
1≦B<W 1 ≦ B < W

错误思路

考试时看到这道题,根本就没有想到正解！
而我写出一个dp递推式：

f[i][j]=f[i][j−1]+f[i−1][j] f [ i ] [ j ] = f [ i ] [ j − 1 ] + f [ i − 1 ] [ j ]

((1<=i<=H−aand1<=j<=W)or(H−a+1<=i<=HandW−b+1<=j<=W)) ( ( 1 <= i <= H − a a n d 1 <= j <= W ) o r ( H − a + 1 <= i <= H a n d W − b + 1 <= j <= W ) )

Markdown太深奥,我不会用….凑合看吧
边界是

f[i][1]=1(1<=i<=H−a) f [ i ] [ 1 ] = 1 ( 1 <= i <= H − a )

f[1][j]=1(1<=j<=W) f [ 1 ] [ j ] = 1 ( 1 <= j <= W )

但是想想,这种方法虽然空间上可以开滚动数组优化到O(n)级别,但是,时间上优化不了啊！还是O(n^2)级别,所以就TLE了

思路

Find（规律）

好了,正解降临！
如果没有左下角的矩形,我们是不是稍稍举个例子就能发现一点规律？
我们举一个H为4，W为5,到每个点方案数的例子：

看看看！看到没有那里有一个(4,6,4,1)是不是很熟悉？？好像是(1,4,6,4,1)吧？
好像我们在哪里见到过，杨辉三角！

我们就可以对刚刚那个例子操作一下：

是不是就是杨辉三角放倒了？
然后我们知道杨辉三角与组合(C)密切相关,于是我们就可以开始考虑组合方面的问题了.

组合计数

如上图,我们可以将s->t的路径分为s->i->t，i在H-a那一行,那么我们就显然可以得出i在横向位置方面的取值范围:

b+1<=i<=W b + 1 <= i <= W

①s->i
我们可以知道,s->i的总步数，在横向上移动步数,纵向上移动步数是固定的：
s->i纵向上步数：H-a-1
s->i横向上步数：i-1
s->i总步数：H-a+i-2
那么我们或许不能理解怎么算,那我们可以想象一下(imagine!):

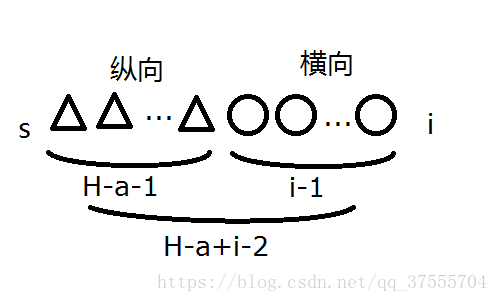
图中三角形代表往下走一步,圆形代表往右走一步,那么不妨让每次操作记为(1,2,…,H-a+i-2)，一共有这么多次,而我们要在其中选H-a-1个放H-a-1个三角形,那么剩下的是不是就都是圆形？H-a+i-2中选出H-a-1个,是不是就是C(H-a+i-2,H-a-1)或者是C(H-a+i-2,i-1)

②i->t
跟①一样我们来计算一下i->t的步数:
i->t纵向上步数：a
i->t横向上步数：W-i
i->t总步数：a+W-i
But
我们可以发现,如果我们这样干的话会重复计数,比如当前i再往右走一步,就和i+1的方案数重复了于是,到了i只能往下走.于是我们可一发现,这里(H-a+1,i)->(H,W)的方案数就是(H-a,i)->(H,W)的方案数，所以纵向上是a-1步而不是a步,于是这里应该为：
i->t纵向上步数：a-1
i->t横向上步数：W-i
i->t总步数：W+a-i-1
所以应该是：C(W+a-i-1,a-1)或C(W+a-i-1,W-i)(计算方法同上)

总方案就是

Sum{C(H−a+i−2,H−a−1)∗C(W+a−i−1,a−1)}(b+1<=i<=W) S u m { C ( H − a + i − 2 , H − a − 1 ) ∗ C ( W + a − i − 1 , a − 1 ) } ( b + 1 <= i <= W )

乘法逆元

这个嘛,哼哼哼,学了之后发现MOD是’套路’质数后就简单许多,这里使用来算C(排列)的,乘法逆元部分详见博主另一篇博客,自我感觉比较详细~~..,好吧,我承认,我把最重要的另一部分放在了另一篇博客增加阅读量……那篇博客中这道题会出现成为两道乘法逆元实现例子之一…(**超级打广告**)

代码

#include  
#include
#include  
#include  
#include  
#include  
#include  
#include 
#include
#include
#include 
using namespace std; 
#define MOD 1000000007
#define MAXN 100000
#define LL long long
#define INF 0x3f3f3f3f
LL read(){ 
    LL f=1,x=0; 
    char c=getchar(); 
    while(c<'0'||'9'if(c=='-')f=-1;c=getchar();} 
    while('0'<=c&&c<='9'){x=x*10+c-'0';c=getchar();} 
    return f*x; 
}
LL n,h,w,a,b,s[2*MAXN+5]={1},inv[2*MAXN+5];
LL QuPow(LL x,LL y){//快速幂
    LL ret=1;
    while(y){
        if(y&1) ret=ret*x%MOD;
        x=x*x%MOD;
        y>>=1;
    }
    return ret;
}
void Prepare(){//乘法逆元处理
    for(int i=1;i<=2*MAXN;i++) s[i]=s[i-1]*i%MOD;
    inv[0]=1;
    inv[2*MAXN]=QuPow(s[2*MAXN],MOD-2);
    for(int i=2*MAXN-1;i>=1;i--)
        inv[i]=inv[i+1]*(i+1)%MOD;
    return ;
}
LL C(LL m,LL n){//计算排列
    return s[m]*inv[n]%MOD*inv[m-n]%MOD;
}
int main(){
    LL ans=0;
    Prepare();
    h=read(),w=read(),a=read(),b=read();
    for(int i=b+1;i<=w;i++)//推导计数方法
        ans=(ans+C(h-a+i-2,i-1)*C(a+w-i-1,a-1)%MOD)%MOD;
    printf("%lld\n",ans);
    return 0;
}