【数据结构】--- 二叉树的递归遍历和非递归遍历【C语言实现】
目录
1. 创建一颗二叉树
2.递归前序遍历二叉树
3.递归中序遍历二叉树
4.递归后序遍历二叉树
5. 测试递归打印二叉树代码
6. 非-递归前序遍历二叉树
7. 非-递归实现中序遍历二叉树
8. 非 - 递归实现后序遍历【较为复杂的方法】
9. 非 - 递归实现后序遍历【简单的方法】
10. 二叉树的层次遍历
11. 最后:附全部代码:
对于二叉树的非递归 深度优先遍历,使用的都是栈
对于二叉树的层次遍历,使用的是队列
1. 创建一颗二叉树
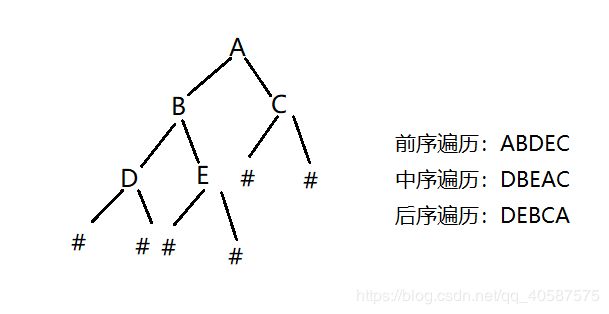
依据前序遍历创建二叉树:,树结构如上图所示
输入: ABD##E##C##
#include
#include
// 二叉树的实现
// 定义 二叉树的 结构体
typedef struct node{
char data;
struct node *left;
struct node *right;
}Node, *Tree;
// 依据前序遍历创建二叉树
// 根左右: ABD##E##C##
Tree create_tree(){
Node *root = NULL;
char ch;
scanf("%c", &ch); // 输入 ABD##E##C##
if (ch != '#'){
root = (Node*)malloc(sizeof(Node));
root->data = ch;
root->left = create_tree(); // 递归创建
root->right = create_tree();
}
else{
root = NULL;
}
return root;
}
2.递归前序遍历二叉树
// 递归前序遍历二叉树
void preOrderRec(Tree root){
if (root != NULL){
printf(" %c - ", root->data);
preOrderRec(root->left);
preOrderRec(root->right);
}
}3.递归中序遍历二叉树
// 递归中序遍历二叉树
void inOrderRec(Tree root){
if (root != NULL){
inOrderRec(root->left);
printf(" %c - ", root->data);
inOrderRec(root->right);
}
}4.递归后序遍历二叉树
void backOrderRec(Tree root){
if (root != NULL){
backOrderRec(root->left);
backOrderRec(root->right);
printf(" %c - ", root->data);
}
}5. 测试递归打印二叉树代码
int main(){
printf("starting ------ \n");
Tree root = create_tree();
printf("递归前序遍历--- \n");
preOrderRec(root);
printf("\n");
printf("递归中序遍历--- \n");
inOrderRec(root);
printf("\n");
printf("递归后序遍历--- \n");
backOrderRec(root);
printf("\n");
return 0;
}6. 非-递归前序遍历二叉树
前序遍历顺序是:根-左-右
先打印根节点的值,由于栈是先进后出,所以先将 右子树放进去,再将左子树放进去
// 非-递归前序遍历二叉树
void preOrderNRec(Tree root){
Tree stack[MAXSIZE], node;
int k = -1;
if (root == NULL){
printf("tree is empty-- \n");
return;
}
else{
k++;
// 仿照一个栈
stack[k] = root; // 将根节点入栈
while (k > -1){
//出栈
node = stack[k--];
printf(" %c - ", node->data);
// 先把右子树放进去,栈是先进去后出,所以下面的左子树先出
if (node->right != NULL){
stack[++k] = node->right;
}
if (node->left != NULL){
stack[++k] = node->left;
}
}
}
}7. 非-递归实现中序遍历二叉树
中序遍历的非递归方式实现思想是:
1. 从根结点开始,遍历左孩子同时压栈,当遍历结束,说明当前遍历的结点没有左孩子,
2. 从栈中取出来调用操作函数,然后访问该结点的右孩子,继续以上重复性的操作。
// 非-递归实现中序遍历二叉树
void inOrderNRec(Tree root){
Tree stack[MAXSIZE], node;
int top = 0;
// 判断树是否为空
if (root == NULL){
printf("tree is empty-- \n");
return;
}
node = root;
while (node != NULL || top > 0){
// 将所有的左子树节点入栈
while (node != NULL){
stack[++top] = node;
node = node->left;
}
// 如果右节点为空的话,执行下列语句
node = stack[top--];
printf(" %c - ", node->data);
// 扫描右节点
node = node->right;
}
}8. 非 - 递归实现后序遍历【较为复杂的方法】
void backOrderNRec(Tree root){
Node *p = root;
Node *stack[MAXSIZE];
int num = 0;
Node *have_visited = NULL;
while (NULL != p || num>0)
{
while (NULL != p)
{
stack[num++] = p;
p = p->left;
}
p = stack[num - 1];
if (NULL == p->right || have_visited == p->right)
{
printf(" %c - ", p->data);
num--;
have_visited = p;
p = NULL;
}
else
{
p = p->right;
}
}
}9. 非 - 递归实现后序遍历【简单的方法】
非递归实现后序遍历还是很复杂的,变来变去,指来指去的
但是,我发现一种简单的方法
我们知道 后序遍历的顺序为:
后序:左->右->根
那么可以把后序当作:根->右->左,最后再反转回来即可。
由于我们是使用的栈,所以先保存根节点, 然后先放进去 左节点,再放 进去 右节点
void backOrderNRecSimple(Tree root){
Tree stack[MAXSIZE], node;
int top = 0;
int count = 0;
char array[MAXSIZE]; // 使用一个数组来保存数据,方便最后数组的反转
if (root == NULL){
printf("tree is empty-- \n");
return;
}
else{
top++;
// 仿照一个栈
stack[top] = root; // 将根节点入栈
while (top > 0){
//出栈
node = stack[top--];
array[count++] = node->data; // 将其保存在一个数组当中
// 先把右子树放进去,栈是先进去后出,所以下面的左子树先出
if (node->left != NULL){
stack[++top] = node->left; // 入栈
}
if (node->right != NULL){
stack[++top] = node->right;
}
}
}
// 反转数组,输出
for (int i = count-1; i >= 0; i--){
printf(" %c - ", array[i]);
}
}附上java代码,更为简单:
ArrayList postOrder(TreeNode root) {
ArrayList list = new ArrayList();
if (root != null) {
Stack stack = new Stack();
stack.push(root);
while (!stack.isEmpty()) {
TreeNode node = stack.pop();
list.add(node.val);
if (node.left != null) {
stack.push(node.left);
}
if (node.right != null) {
stack.push(node.right);
}
}
//反转
Collections.reverse(list);
}
return list;
}
10. 二叉树的层次遍历
层次遍历使用的是 队列来实现
void Level_traversal(Tree root){
if (root == NULL){
printf("tree is empty-- \n");
return;
}
Tree stack[MAXSIZE], node;
node = root;
int front = 0; // 使用 front, rear模拟队列
int rear = 0;
stack[rear++] = node;
while (front != rear){
node = stack[front++]; // 模拟队列,先获取front当前元素,然后在指向 front ++ 位元素
printf(" %c - ", node->data);
// 左右子树入队列
if (node->left != NULL){
stack[rear++] = node->left;
}
if (node->right != NULL){
stack[rear++] = node->right;
}
}
}
11. 最后:附全部代码:
#include
#include
#define MAXSIZE 100
// 二叉树的实现
// 定义 二叉树的 结构体
typedef struct node{
char data;
struct node *left;
struct node *right;
}Node, *Tree;
// 依据前序遍历创建二叉树
// 根左右: ABD##E##C##
Tree create_tree(){
Node *root = NULL;
char ch;
scanf("%c", &ch); // 输入 ABD##E##C##
if (ch != '#'){
root = (Node*)malloc(sizeof(Node));
root->data = ch;
root->left = create_tree(); // 递归创建
root->right = create_tree();
}
else{
root = NULL;
}
return root;
}
// 递归前序遍历二叉树
void preOrderRec(Tree root){
if (root != NULL){
printf(" %c - ", root->data);
preOrderRec(root->left);
preOrderRec(root->right);
}
}
// 非-递归前序遍历二叉树
void preOrderNRec(Tree root){
Tree stack[MAXSIZE], node;
int top = 0;
if (root == NULL){
printf("tree is empty-- \n");
return;
}
else{
top++;
// 仿照一个栈
stack[top] = root; // 将根节点入栈
while (top > 0){
//出栈
node = stack[top--];
printf(" %c - ", node->data);
// 先把右子树放进去,栈是先进去后出,所以下面的左子树先出
if (node->right != NULL){
stack[++top] = node->right; // 入栈
}
if (node->left != NULL){
stack[++top] = node->left;
}
}
}
}
// 递归中序遍历二叉树
void inOrderRec(Tree root){
if (root != NULL){
inOrderRec(root->left);
printf(" %c - ", root->data);
inOrderRec(root->right);
}
}
// 非-递归实现中序遍历二叉树
void inOrderNRec(Tree root){
Tree stack[MAXSIZE], node;
int top = 0;
// 判断树是否为空
if (root == NULL){
printf("tree is empty-- \n");
return;
}
node = root;
while (node != NULL || top > 0){
// 将所有的左子树节点入栈
while (node != NULL){
stack[++top] = node;
node = node->left;
}
// 如果右节点为空的话,执行下列语句
node = stack[top--];
printf(" %c - ", node->data);
// 扫描右节点
node = node->right;
}
}
// 递归后序遍历二叉树
void backOrderRec(Tree root){
if (root != NULL){
backOrderRec(root->left);
backOrderRec(root->right);
printf(" %c - ", root->data);
}
}
// 非 - 递归实现后序遍历
void backOrderNRec(Tree root){
Node *p = root;
Node *stack[MAXSIZE];
int num = 0;
Node *have_visited = NULL;
while (NULL != p || num>0)
{
while (NULL != p)
{
stack[num++] = p;
p = p->left;
}
p = stack[num - 1];
if (NULL == p->right || have_visited == p->right)
{
printf(" %c - ", p->data);
num--;
have_visited = p;
p = NULL;
}
else
{
p = p->right;
}
}
}
void backOrderNRecSimple(Tree root){
Tree stack[MAXSIZE], node;
int top = 0;
int count = 0;
char array[MAXSIZE]; // 使用一个数组来保存数据,方便最后数组的反转
if (root == NULL){
printf("tree is empty-- \n");
return;
}
else{
top++;
// 仿照一个栈
stack[top] = root; // 将根节点入栈
while (top > 0){
//出栈
node = stack[top--];
array[count++] = node->data; // 将其保存在一个数组当中
// 先把右子树放进去,栈是先进去后出,所以下面的左子树先出
if (node->left != NULL){
stack[++top] = node->left; // 入栈
}
if (node->right != NULL){
stack[++top] = node->right;
}
}
}
// 反转数组,输出
for (int i = count-1; i >= 0; i--){
printf(" %c - ", array[i]);
}
}
// 层次遍历,打印出二叉树的值
void Level_traversal(Tree root){
if (root == NULL){
printf("tree is empty-- \n");
return;
}
Tree stack[MAXSIZE], node;
node = root;
int front = 0; // 使用 front, rear模拟队列
int rear = 0;
stack[rear++] = node;
while (front != rear){
node = stack[front++]; // 模拟队列,先获取front当前元素,然后在指向 front ++ 位元素
printf(" %c - ", node->data);
// 左右子树入队列
if (node->left != NULL){
stack[rear++] = node->left;
}
if (node->right != NULL){
stack[rear++] = node->right;
}
}
}
int main(){
printf("starting ------ \n");
Tree root = create_tree();
printf("递归前序遍历--- \n");
preOrderRec(root);
printf("\n");
printf("递归中序遍历--- \n");
inOrderRec(root);
printf("\n");
printf("递归后序遍历--- \n");
backOrderRec(root);
printf("\n");
printf("------------------\n");
printf("非递归实现前序遍历--- \n");
preOrderNRec(root);
printf("\n");
printf("非递归实现中序遍历--- \n");
inOrderNRec(root);
printf("\n");
printf("非递归实现后序遍历--- \n");
backOrderNRec(root);
printf("\n");
printf("非递归实现后序遍历 简单的方法 --- \n");
backOrderNRecSimple(root);
printf("\n");
printf("层次遍历 --- \n");
Level_traversal(root);
printf("\n");
// ABD##E##C##
return 0;
}