R语言对数据进行非参数检验
假设检验:参数检验运用样本的统计量来估计总体的参数,如用样本均值估计总体均值,用样本标准差估计总体标准差。
非参数检验则不考虑数据的具体值,而更多地运用了数据大小排序的信息,因此不可能以此估计总体的参数
1.原假设和备择假设
同时在实际应用中,我们有不同的需求,因此又有双侧检验和单侧检验的区分。
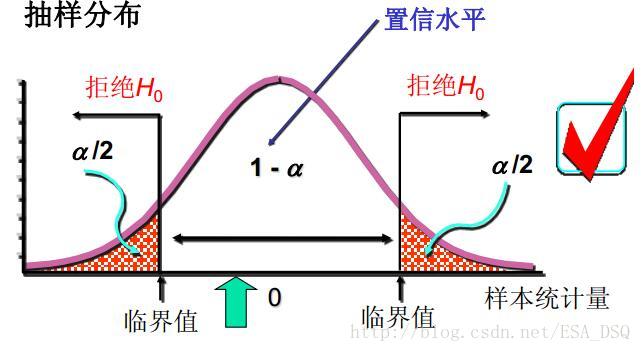
- 双侧检验——备择假设没有特定的方向性,并含有符号“=”的假设检验,称为双侧检验或双尾检验(two-tailed test)
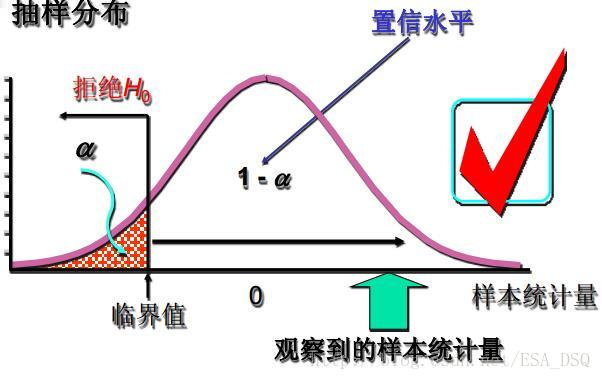
- 单侧检验——备择假设具有特定的方向性,并含有符号“>”或“<”的假设检验,称为单侧检验或单尾检验(one-tailed test)。其中备择假设的方向为“<”,称为左侧检验,备择假设的方向为“>”,称为右侧检验。
原假设与备择假设形式:
双侧检验:
左侧检验:
2.非参数检验:
1.正态W检验
例1. 已知15名学生体重如下,问是否服从正态分布
![]()
解:
R语言代码:
w <- c(75.0, 64.0, 47.4, 66.9, 62.2, 62.2, 58.7, 63.5,
66.6, 64.0, 57.0, 69.0, 56.9, 50.0, 72.0)
shapiro.test(w)
P值>0.05,接受原假设,认为来自正态分布总体。
例2 :H0:数据集服从正态分布
H1:数据集不服从正态分布
#是否服从正态分布
#随机抽取3000个样本
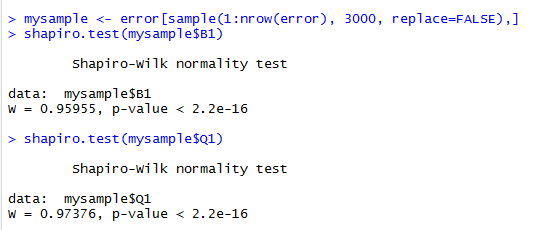
mysample <- error[sample(1:nrow(error), 3000, replace=FALSE),]
shapiro.test(mysample$B1)
shapiro.test(mysample$Q1)#显示p值小于2.2e-16,因此认为不服从正太分布
2.Kolmogorov-Smirnov 检验
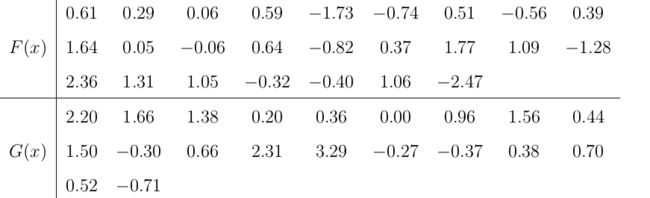
例3. 假定从分布函数未知的F(x)和G(x)的总体中分别抽出25个和20个观察值的随即样品,其数据由下表所示。现检验F(x)和G(x)是否相同。
R语言代码:
X<-scan( )
0.61 0.29 0.06 0.59 -1.73 -0.74 0.51 -0.56
1.64 0.05 -0.06 0.64 -0.82 0.37 1.77
2.36 1.31 1.05 -0.32 -0.40 1.06 -2.47
0.39 1.09 -1.28
Y<-scan( )
2.20 1.66 1.38 0.20 0.36 0.00
0.96 1.56 0.44 1.50 -0.30 0.66
2.31 3.29 -0.27 -0.37 0.38 0.70
0.52 -0.71
ks.test(X,Y)
P值>0.05,无法拒绝原假设,说明F(x)和G(x)分布函数相同。
例子:
> ks.test(error$B1,error$Q1)
Two-sample Kolmogorov-Smirnov test
data: error$B1 and error$Q1
D = 0.11508, p-value < 2.2e-16
alternative hypothesis: two-sided Two-sample Kolmogorov-Smirnov test
data: error$B1 and error$Q1
D = 0.11508, p-value < 2.2e-16
alternative hypothesis: two-sidedP值<0.05,可以拒绝原假设,说明B1,Q1分布函数相同。
3.列联表数据的检验
例4. 为了研究吸烟是否与患肺癌相关,对63位肺癌患者及43名非肺癌患者(对照组)调查了其中的吸烟人数,得到2x2列联表,如下表所示
解:
进行Pearson卡方检验
R语言代码:
x<-c(60, 3, 32, 11)
dim(x)<- c(2,2)
chisq.test(x,correct = F)
P值<0.05,拒绝原假设,认为吸烟与患肺癌相关。
4.符号检验
例5. 用两种不同的饲料养猪,其增重情况如下表所示。试分析两种饲料养猪有无显著差异。
R语言代码:
x<-scan()
25 30 28 23 27 35 30 28 32 29 30 30 31 16
y<-scan()
19 32 21 19 25 31 31 26 30 25 28 31 25 25
binom.test(sum(x
sum(x < y)表示样品X小于样品Y的个数。计算出P值大于0.05,无法拒绝原假设,可以认为两种饲料养猪无显著差异。
例子6:H0:两组数据无显著的差别
H1:两组数据有明显的差别
binom.test(sum(error$B1> binom.test(sum(error$B1P<0.05,所以拒绝原假设,接受两组数据有明显的差别
在符号检验法中,只计算符号的个数,而不考虑每个符号差所包含的绝对值的大小,因此常常使用弥补了这个缺点的wilcoxon符号秩检验。
5.符号秩检验
在R语言中进行符号秩检验可以使用wilcox.test( )
wilcox.test(x, y = NULL,
alternative = c("two.sided", "less", "greater"),
mu = 0, paired = FALSE, exact = NULL, correct = TRUE,
conf.int = FALSE, conf.level = 0.95, ...)
n为整数向量,表示试验的次数,当x为矩阵时,该值无效.
p为向量,表示试验成功的概率,必须与x有相同的维数,且值在0至1之间,默认值为NULL.
alternative为备择假设选项,取"two.sided"(默认值)表示双侧检验;取"less"表示备择假设为“<”的单侧检验,取"greater"表示备择假设为“>”的单侧检验.
conf.level为0~1之间的数值(默认值为0.95),表示置信水平,它将用于计算比率p或比率差p1-p2的置信区间.
correct为逻辑变量,表示是否对统计量作连续修正,默认值为TRUE.
其中x,y是观察数据构成的数据向量。alternative是备择假设,有单侧检验和双侧检验,mu待检参数,如中位数M0.paired是逻辑变量,说明变量x,y是否为成对数据。exact是逻辑变量,说明是否精确计算P值,当样本量较小时,此参数起作用,当样本两较大时,软件采用正态分布近似计算P值。correct是逻辑变量,说明是否对P值的计算采用连续性修正,相同秩次较多时,统计量要校正。conf.int是逻辑变量,说明是否给出相应的置信区间。
------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
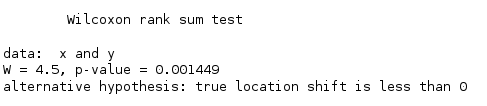
例7. 今测得10名非铅作业工人和7名铅作业工人的血铅值,如下表所示。试用Wilcoxon秩和检验分析两组工人血铅值有无差异。
解:进行Wilcoxon秩和检验R语言同样可以使用wilcox.test( )
R语言代码:
x<-c(24, 26, 29, 34, 43, 58, 63, 72, 87, 101)
y<-c(82, 87, 97, 121, 164, 208, 213)
wilcox.test(x,y,alternative="less",exact=FALSE,correct=FALSE)
P值小于0.05,拒绝原假设,即铅作业工人血铅值高于非作业工人。
例子2:H0:两组数据无显著的差别
H1:两组数据有明显的差别
> wilcox.test(error$B1,error$Q1,alternative="two.sided",exact=FALSE,correct=TRUE)
Wilcoxon rank sum test with continuity correction
data: error$B1 and error$Q1
W = 2103600000, p-value = 1.606e-10
alternative hypothesis: true location shift is not equal to 0P<0.05,所以拒绝原假设,两组数据是有差别的
6.二元数据相关检验
例8 .某种矿石中两种有用成分A,B,取10个样品,每个样品中成分A的含量百分数x(%),及B的含量百分数y(%)的数据下表所示,对两组数据进行相关性检验。
解:进行相关性检验,在R语言中可以使用cor.test( )
cor.test(x, y,
alternative = c("two.sided", "less", "greater"),
method = c("pearson", "kendall", "spearman"),
exact = NULL, conf.level = 0.95, ...)
#其中x,y是数据长度相同的向量,alternative是备择假设,缺省值为"two.sided",method是检验方法,缺省值是Pearson检验,conf.level是置信区间水平,缺省值为0.95
cor.test( )还有另一种使用格式
cor.test(formula, data, subset, na.action, ...) #其中formula是公式,形如'~u+v' , 'u', 'v' 必须是具有相同长度的数值向量,data是数据框,subset是可选择向量,表示观察值的子集。
假设此例中两组数据均来自正态分布,使用pearson相关性检验,
R语言代码:
ore<-data.frame(
x=c(67, 54, 72, 64, 39, 22, 58, 43, 46, 34),
y=c(24, 15, 23, 19, 16, 11, 20, 16, 17, 13)
)
cor.test(ore$x,ore$y)
可见P值<0.05,拒绝原假设,认为X与Y相关。
![]()