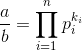Educational Codeforces Round 85 (Rated for Div. 2)

http://codeforces.com/contest/1334

---

A - Level Statistics

阅读理解题。

满足第一个数字大于等于第二个数字，第一个数字和第二个数字都递增，第一个数字的增量不能小于第二个数字的增量就是 YES

#include 
#define ll long long
#define sc scanf
#define pr printf
using namespace std;
const int MAXN = 2e5 + 5;
int aa[105][2];
int main()
{
	int T = 1;
	sc("%d", &T);
	while (T--)
	{
		int n;
		sc("%d", &n);
		int a, b, q, w;
		n--;
		sc("%d%d", &q, &w);
		for (int i = 0; i < n; i++)
		{
			sc("%d%d", &aa[i][0], &aa[i][1]);
		}
		if (q < w)
		{
			pr("NO\n");
			goto qwe;
		}
		for (int i = 0; i < n; i++)
		{
			a = aa[i][0];
			b = aa[i][1];
			if (a < b)
			{
				pr("NO\n");
				goto qwe;
			}
			if (b < w || a < q)
			{
				pr("NO\n");
				goto qwe;
			}
			if (a - q < b - w)
			{
				pr("NO\n");
				goto qwe;
			}
			q = a, w = b;
		}
		pr("YES\n");
		qwe:;
	}
}

B - Middle Class

贪心，找到最多的人，使得他们的平均值大于 x

#include 
#define ll long long
#define sc scanf
#define pr printf
using namespace std;
const int MAXN = 1e5 + 5;
ll a[MAXN];
int main()
{
	int T = 1;
	sc("%d", &T);
	while (T--)
	{
		int n; ll x;
		sc("%d%lld", &n, &x);
		ll sum = 0;
		for (int i = 1; i <= n; i++)
			sc("%lld", &a[i]);
		sort(a + 1, a + 1 + n, greater());
		ll num = 0;
		while (num < n)
		{
			num++;
			sum += a[num];
			if (sum < x * num)
			{
				pr("%lld\n", num - 1);
				goto qwe;
			}
		}
		pr("%d\n", n);
	qwe:;
	}
}

C - Circle of Monsters

算出上一个爆炸后，下一个爆炸需要的花费和，然后枚举从哪个位置开始即可

#include
#define ll long long
using namespace std;
const int N = 3e5 + 10;
ll a[N], b[N], sum;
int main()
{
	int T;
	scanf("%d", &T);
	while (T--) {
		int n;
		scanf("%d", &n);
		for (int i = 1; i <= n; i++)
			scanf("%lld %lld", &a[i], &b[i]);
		sum = max(0LL, a[1] - b[n]);
		for (int i = 2; i <= n; i++)
			sum += max(0LL, a[i] - b[i - 1]);
		ll ans = sum + a[1] - max(0LL, a[1] - b[n]);
		for (int i = 2; i <= n; i++)
			ans = min(ans, sum + a[i] - max(0LL, a[i] - b[i - 1]));
		printf("%lld\n", ans);
	}
}

D - Minimum Euler Cycle

规律题。

感觉Note已经暗示的很明显了，比如 5 的构造方法就是

1 2 1 3 1 4 1 5

2 3 2 4 2 5

3 4 3 5

4 5

1

除了最后一个 1 需要特判，其他的都可以直接算出来

#include 
#define ll long long
#define sc scanf
#define pr printf
using namespace std;
const int MAXN = 3e5 + 5;
ll a[MAXN], b[MAXN];
bool book[MAXN];
int main()
{
	int T = 1;
	sc("%d", &T);
	while (T--)
	{
		ll n, l, r;
		sc("%lld%lld%lld", &n, &l, &r);
		ll sum = 1;
		for (int i = 1; i < n; i++)
		{
			if (sum + (n - i) * 2 >= l)
			{
				for (int j = i + 1; j <= n; j++)
				{
					if (sum >= l && sum <= r)
						pr("%d ", i);
					sum++;
					if (sum >= l && sum <= r)
						pr("%d ", j);
					sum++;
					if (sum > r)
						goto qwe;
				}
			}
			else
			{
				sum = sum + (n - i) * 2;
			}
			if (sum > r)
				break;
		}
		if (sum == r)
			pr("1 ");
	qwe:;
		pr("\n");
	}
}

E - Divisor Paths

有个结论：          （不会证）

所以我们只需要考虑这个数字有几种方法到达他的那个因数

考虑到每一条边都是除以一个质因数，所以只需要将  质因数分解，求出不同排列的个数即可

，

由于每个点都是 D 的因数，所以没有必要每次都枚举要求的点的因数，直接在 D 的因数里面找是他因数的个数即可

#include 
#define ll long long
#define sc scanf
#define pr printf
using namespace std;
vectorv;
void get(ll n)
{
	for (ll i = 2; i * i <= n; i++)
	{
		if (n % i == 0)
		{
			while (n % i == 0)
				n /= i;
			v.push_back(i);
		}
	}
	if (n > 1)
		v.push_back(n);
}
ll gcd(ll a, ll b)
{
	return b == 0 ? a : gcd(b, a % b);
}
ll fac[105], inv[105];
const ll mod = 998244353;
ll num[30];
ll power(ll a, ll b)
{
	ll res = 1;
	while (b)
	{
		if (b & 1)
			res = res * a % mod;
		a = a * a % mod;
		b >>= 1;
	}
	return res;
}
void init()
{
	fac[0] = fac[1] = 1;
	inv[0] = inv[1] = 1;
	for (int i = 2; i <= 100; i++)
	{
		fac[i] = fac[i - 1] * i % mod;
		inv[i] = power(fac[i], mod - 2);
	}
}
ll calc(ll a, ll b)
{
	memset(num, 0, sizeof(num));
	int cnt = 0;
	for (int i = 0; i < v.size(); i++)
	{
		while (a % v[i] == 0)
		{
			cnt++;
			num[i]++;
			a /= v[i];
		}
		while (b % v[i] == 0)
		{
			cnt--;
			num[i]--;
			b /= v[i];
		}
	}
	ll ans = fac[cnt];
	for (int i = 0; i < v.size(); i++)
		if (num[i])
			ans = ans * inv[num[i]] % mod;
	return ans;
}
int main()
{
	init();
	ll d;
	sc("%lld", &d);
	get(d);
	int q;
	sc("%d", &q);
	while (q--)
	{
		ll a, b;
		sc("%lld%lld", &a, &b);
		ll c = gcd(a, b);
		ll ans = calc(a, c) * calc(b, c) % mod;
		pr("%lld\n", ans);
	}
}