2019杭电多校第五场
没有完成签到……
场上三题:
1004:equation
给你n个ai和bi,给你C,求解方程:
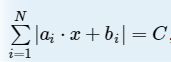
画个图可以发现,每两个零点之间的区域都对应一个一元一次方程,把这些零点排序之后可以很容易得到每个区间的方程,每个区间都解一个一元一次方程,然后判断解是否在这个区间内。要特判a=0的情况。
#include
#define ll long long
#define P pair
using namespace std;
const int maxn = 1e5 + 50;
struct node{
ll a, b;
bool operator < (const node& x){
return -b*x.a < -x.b*a;
}
}e[maxn];
ll C;
int n;
vector ans;
int main()
{
int T;
cin>>T;
while(T--){
cin>>n>>C;
ans.clear();
ll a = 0, b = 0;
for(int i = 0; i < n; ++i) {
scanf("%lld%lld", &e[i].a, &e[i].b);
a -= e[i].a;
b -= e[i].b;
}
sort(e, e+n);
int bad = 0;
if(a < 0){
if( (C-b)*e[0].a >= -e[0].b*a ) ans.push_back( P(b-C, -a) );
}
else if(a == 0){
if(C == b) bad = 1;
}
else{
if((C-b)*e[0].a <= -e[0].b*a) ans.push_back( P(C-b, a) );
}
for(int i = 0; i < n-1; ++i){//n-1个间隔
a += 2*e[i].a;
b += 2*e[i].b;
if(e[i].a == e[i+1].a && e[i].b == e[i+1].b) continue;
if(a < 0){
if((C-b)*e[i+1].a >= -e[i+1].b*a && (C-b)*e[i].a < -e[i].b*a ){
ans.push_back(P(b-C, -a));
}
}
else if(a == 0){
if(C == b) bad = 1;
}
else{
if((C-b)*e[i+1].a <= -e[i+1].b*a && (C-b)*e[i].a > -e[i].b*a){
ans.push_back(P(C-b, a));
}
}
}
a += 2*e[n-1].a;
b += 2*e[n-1].b;
if(a < 0){
if( (C-b)*e[n-1].a < -e[n-1].b*a ) ans.push_back( P(b-C, -a) );
}
else if(a == 0){
if(C == b) bad = 1;
}
else{
if((C-b)*e[n-1].a > -e[n-1].b*a) ans.push_back( P(C-b, a) );
}
if(bad){
printf("-1\n"); continue;
}
printf("%d", ans.size());
for(int i = 0; i < ans.size(); ++i){
a = ans[i].first;
b = ans[i].second;
if(a == 0){
printf(" 0/1");continue;
}
if(b < 0) b*=-1, a*=-1;
ll t = __gcd(abs(a), abs(b));
b/=t; a/=t;
printf(" %lld/%lld",a, b);
}
cout<
1005:permutation 1
你需要求一个长度为n的排列,使得这个排列的差分数组在所有差分数组中的字典序为第k大。k<=(10000,n!)
看到k最多为10000,意味着暴搜最多搜到10000个叶子。考虑搜索方式。
我们枚举当前位置i填的数字ai与第一位数字a1的差值。
设第一个数为a1,你要填的当前位置是i,你要让 a i − a i − 1 a_i-a_{i-1} ai−ai−1最小,由因为前面的差值都固定了,也就是 a 2 − a 1 , a 3 − a 2 . . , a i − 1 − a i − 2 a_2-a_1,a_3-a_2..,a_{i-1}-a_{i-2} a2−a1,a3−a2..,ai−1−ai−2这些都固定了,相当于你只要让 a i − a 1 a_i-a_1 ai−a1最小,也就让 a i − a i − 1 a_i-a_{i-1} ai−ai−1最小了。每次选择一个差值之后都可能改变下一个位置可以枚举的上界/下界。每次搜到的结果都是除了前面搜到的结果之外字典序最小的。搜到k个的时候跳出,就得到了 a n s ans ans数组,其中 a n s i = a i − a 1 ans_i=a_i-a_1 ansi=ai−a1
Σ a n s i = a 2 + a 3 + . . . + a n − ( n − 1 ) ∗ a 1 = n ( n + 1 ) / 2 − n ∗ a 1 \Sigma ans_i=a_2+a_3+...+a_n-(n-1)*a_1=n(n+1)/2-n*a_1 Σansi=a2+a3+...+an−(n−1)∗a1=n(n+1)/2−n∗a1,解出a1,得到整个排列。
#include
#define ll long long
using namespace std;
int n, k;
set s;
int ans[25];
int cur;
void dfs(int pos, int up, int down){
if(pos == n){
cur++;return;
}
for(int i = down; i <= up; ++i){
if(s.count(i)) continue;
ans[pos] = i;
s.insert(i);
int mi = max(1, 1-i);
int mx = min(n, n-i);
dfs(pos+1, min(up,n-mi), max(down, 1-mx));
s.erase(i);
if(cur == k) return;
}return;
}
int a[25];
int main()
{
int T;cin>>T;
while(T--){
scanf("%d%d", &n, &k);
cur = 0;
s.clear();
s.insert(0);
dfs(1, n - 1, 1 - n);
int sum = 0;
for(int i = 1; i < n; ++i) sum += ans[i];
ans[0] = n*(n+1)/2 - sum;
ans[0]/=n;
printf("%d",ans[0]);
for(int i = 1; i < n; ++i){
printf(" %d", ans[i]+ans[0]);
}printf("\n");
}
}
1007:permutation 2
可以抽象成一条链,每次可以往左/右跳一格或者两格,每个点只能跳一次,求x到y的路径数。
画一画可以发现如果x左边有数字,那么x把左边访问完再回到x+1的路线只能有一条。访问y右边也同理。
如果x左边要访问,访问完以后一定会回x+1,如果y右边有数,要访问完切回到y就必须先到y+1。那么问题变成:
从1到n,每次可以向左/右跳1/2格,要访问所有中间点,求路径数。
设dp[n]为这个问题的解,则dp[n]=dp[n-1]+dp[n-3]。
各种情况讨论讨论。注意x和y相邻且左右都有数要输出0.
#include
#define ll long long
using namespace std;
const ll mod = 998244353;
const int maxn = 1e5 + 50;
ll dp[maxn];
int main()
{
dp[1] = dp[2] = dp[3] = 1;
for(int i = 4; i < maxn; ++i) dp[i] = (dp[i-1] + dp[i-3])%mod;
int T;cin>>T;
while(T--){
int n, x ,y;
scanf("%d%d%d",&n, &x, &y);
if(x > y) swap(x, y);
if(y == x+1){
if(x == 1||y == n) printf("1\n");
else printf("0\n");
continue;
}
if(x == 1 && y == n){
printf("%lld\n", dp[y-x+1]);
}
else if(x == 1|| y == n){
printf("%lld\n",dp[y-x]);
}
else{
printf("%lld\n", dp[y-x-1]);
}
}
}