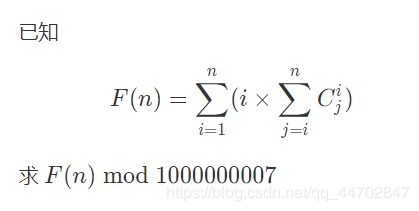字节跳动-文远知行杯 广东工业大学第十四届程序设计竞赛 菜鸡的艰难之旅

字节跳动-文远知行杯 广东工业大学第十四届程序设计竞赛

A- hzy 和 zsl 的生存挑战

32.82% 1000ms 65536K

zsl 和 hzy 来到了臭臭城堡，打算挑战臭臭城堡的大魔王 hyz ，大魔王 hyz 准备让他们进行这样的一个挑战：

挑战开始，zsl 和 hzy 两个人各自来到一间密室，期间两人无法以任何形式交流，期间两人无法以任何形式交流
大魔王 hyz 会随机在两个人的脑海里各发送一个数字，00 或者是 11
zsl 和 hzy 需要猜对对方听到的数字才算通关（当然是在各自的密室中回答的，也就是说回答的时候，zsl 听不到 hzy 的回答，同样，hzy 也听不到 zsl 的），但是大魔王 hyz 觉得人生不能过于无敌，因此降低难度，只要两个人中有一个人答对就算是通关
进行挑战之前，zsl 和 hzy 讨论并制定了一个详细的作战方案，使得自己通关的几率最高，并开始了这次挑战……

显然大魔王 hyz 给这两个人出的数字所有可能的情况有 0000， 0101， 1010， 1111 四种，请按上述枚举的顺序，计算所有情况下 zsl 和 hzy 通关的几率。

Input

(空)

Output

输出四个答案，每个答案后面跟随一个换行符并且保留两位小数位，分别对应 0000， 0101， 1010， 1111的情况下，zsl 和 hzy 通关的几率

样例输入

(空)

样例输出

1.00
0.00
0.50
0.55 (输出仅做格式参考,不保证正确性)

大声bb

这题我还没弄清楚题意呢队友就说全部输出0.75就完事了，我一听这么有自信啊，交呗
结果就，WA，氦，分析了半小时得出这是妥妥的水题，
两个聪明的人加上一个心善的大魔王，只要一个人报听到的数字，另一个人报与听到的数字相反的数字就能百分之百通过啦
AC代码就是直接输出四个1.00

C- 超级无敌简单题

32.74% 1000ms 65536K

通常来说，题面短的题目一般都比较难，所以我要把题面写得很长很长。

通常来说，题面短的题目一般都比较难，所以我要把题面写得很长很长。

通常来说，题面短的题目一般都比较难，所以我要把题面写得很长很长。

鸽子数字由以下过程定义：从任何正整数开始，将数字替换为其各个数位的平方和，并重复该过程，直到该数字等于 11。如果不能，则这个数字不是鸽子数。

例如 77 是鸽子数，因为 7 \to 49 \to 97 \to 130 \to 10 \to 17→49→97→130→10→1

( 7 \times 7 = 497×7=49 , 4 \times 4 + 9 \times 9 = 97 , 9 \times 9 + 7 \times 7 = 130 \cdots4×4+9×9=97,9×9+7×7=130⋯如此类推）

显然 11 是第一个鸽子数。

有 QQ 个询问，每个询问给出一个数 kk ，你需要输出第 kk 个鸽子数。

Input

第一行一个 QQ ，代表询问的个数（ Q \le 100000Q≤100000 ）接下来 QQ 行，每行一个数字 kk（ kk < 150000150000）

Output

每行输出一个数，代表第 kk 个鸽子数

样例输入

2
1
2

样例输出

1
7

大声BB

这题刚拿到的时候想直接暴力，然后打代码的时候发现暴力不起来
原因：不是鸽子数没法直接判断啊omg
后来咬咬牙决定直接判断次数超过20次就拜拜了您
比心A

#include
#include
#include
#include
using namespace std;

long long int G[150005]={0};
long long x=1,y;

void f(){
    for(int i=1;x<150000;i++){
        long long a=i;
        long long k=0;
        int cnt=0;
        while(1){
            if(cnt>=20) break;
            while(a){
               long long b=a%10;
               k=k+b*b;
               a/=10;
            }
            if(k==1){
                G[x++]=i;
                break;
            }
            a=k;
            cnt++;
            k=0;
        }
    }
}
int main()
{
    f();
    int Q,i;
    scanf("%d",&Q);
    while(Q--){
        int k;
        scanf("%d",&k);
        printf("%lld\n",G[k]);
    }
    return 0;
}

G- 简单数学题

30.62% 2000ms 65536K

Input

多组输入，每组输入占一行，包含一个整数 n(1≤n≤10 ^18 )数据不超过 300000组。

Output

对于每组输入，输出一行，包括一个数代表答案。

样例输入

5
100

样例输出 复制

129
660756544

大声BB

这是一道数学题呀，(其实我一直再找规律ahhh好痛苦)
先是发现杨辉三角，然后交，W
然后想办法改进，然后发现也许有更好的办法
幸好我的杨辉三角写的不是很正，然后勉强发现规律，再然后发现规律
然后快速幂运算，然后交，A的时候太开心了咯
期间尝试了各种乱七八糟的思路
导致交上去的代码有一些奇怪的注释
em删掉了一些，保留了一小点点（就是为了证明数学题好痛苦55555）

#include
#include
#include
#include
#include
#include
using namespace std;
typedef long long ll;
const ll mod = 1000000007;
int poww(ll a, ll b) {
    int ans = 1;
	ll  base = a;
    while(b > 0) {
        if(b & 1) {
            ans = (ans * base) % mod;
        }
        base *= base;
        base %= mod;
        b >>= 1;
    }
    return ans % mod;
}
int main()
{
	ll n;
	while(scanf("%lld",&n)!=EOF){
		int ans = 0;
		ll i,j;
//		for(i = 1; i <= n; i++){
//			ans = (ans + i * poww(i-1)) % mod;
//		}
		ans = (n-1) % mod * poww(2,n) % mod +1 ; 
		printf("%d\n",ans);
	}
    return 0;
}