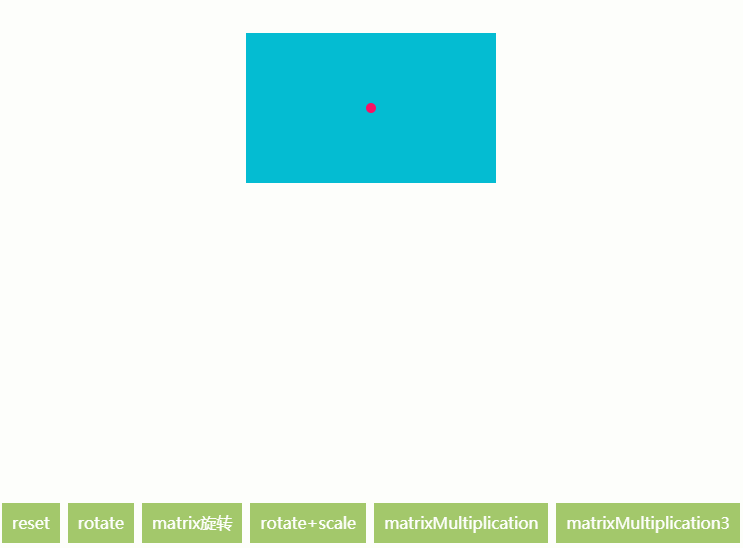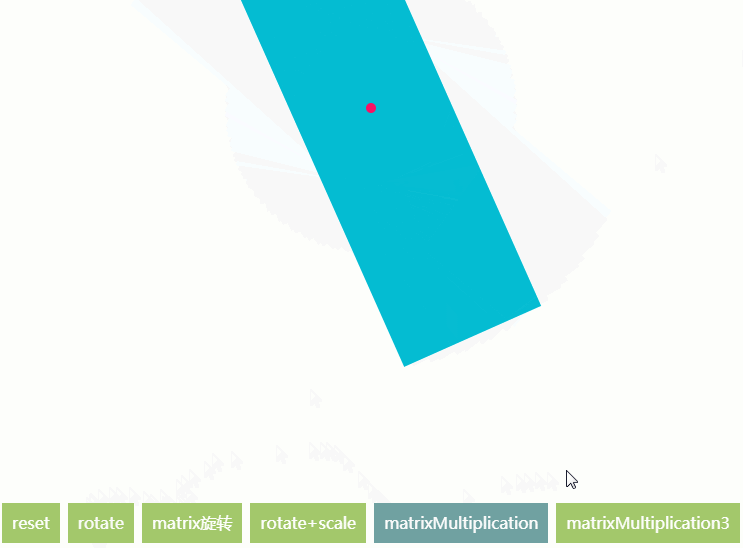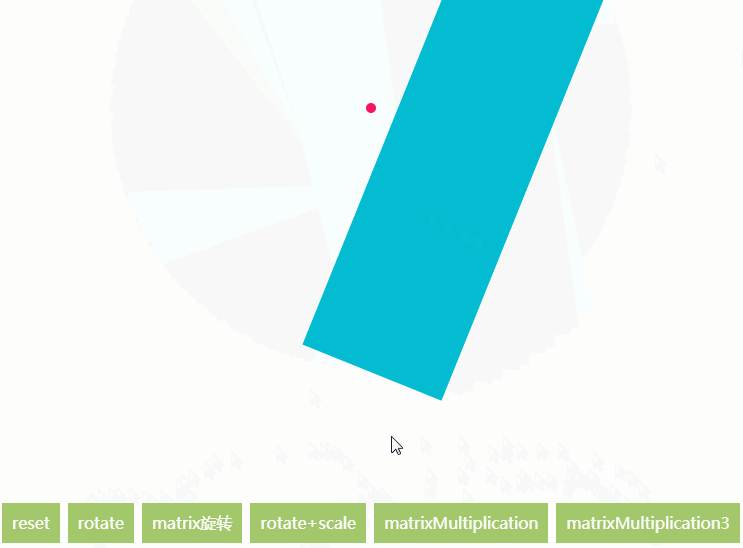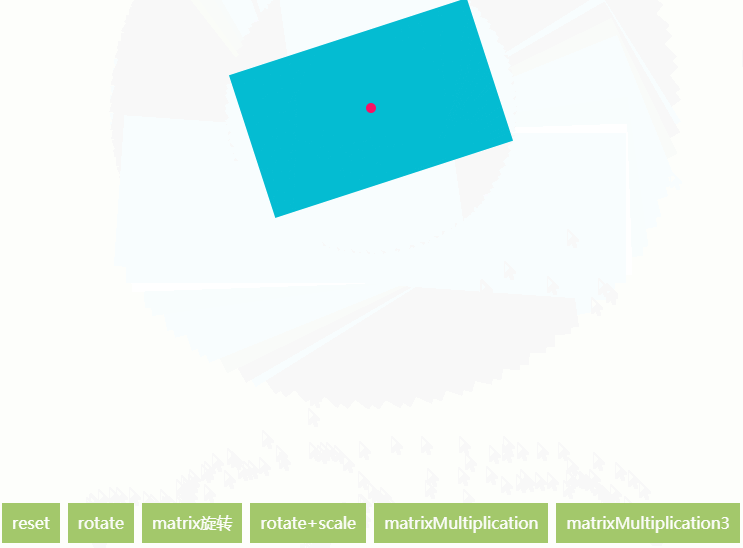
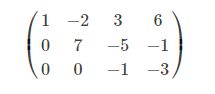对于大多数做动效的人来说,canvas实际应用一般都是2D平面视觉动效,而3D,一般会出动webgl(或者threejs or pixi等,pixi本人也没用过未曾学过),而webgl写起来有点忧伤…繁琐,还要自己写顶点着色器与片元着色器,本人稍微学过一些webgl,从入门到放弃(不过一定会重拾)。
有些时候,我们仅仅是想实现一些3D视觉,但又不想为了一个视觉而加入一个巨大的库(比如threejs),那么这篇文章对你来说可能会有所收获,学会这些,你将对threejs里一些绘制方式的实现有所了解(为什么plane几何体也需要片段参数?为什么全景里纹理贴图总能看出变形无法避免?)
本文将教你从零实现canvas 2d api 实现 3D 图片旋转视觉,相信我,我会讲解的非常详细(特别是对于能用在应用上的知识),毕竟,这是我曾经的分享,图跟demo都是改过一次又一次的
平面透视视觉:
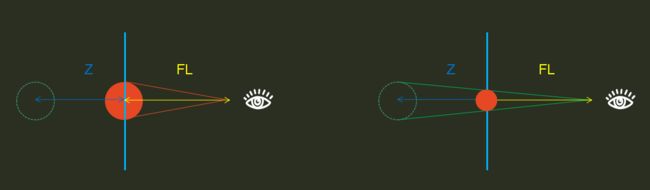
近者大而远着小乎,对于一个图形而言,在空间内,大小不变的情况下,随着Z轴的正向运动(指向屏幕),那么我们会看到物体变得越来越小,反之则越来越大;而对于我们代码而言,需要关心的,是它现在应该绘制成多大。那么对此我们需要推导出一个“缩放比例”
以上图为例,同一个圆,它位于屏幕的大小,我们将它的单位定为1单位,那么在它延Z轴方向运动的时候(左图圆形虚线处),它的投影,在我们视觉当中应该为右图大小,那么此时它的缩放比例((我真的好想好想吐槽这所谓的markdown,该有的都没有啊))
scale = fl / (fl + z)
这条公式怎么得到的?
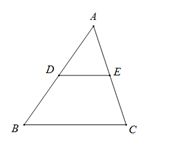
上图为相似三角形,假设BC为原来圆形的大小(参照上一幅图右侧),DE则为投影大小,那么根据相似三角形等比关系,DE:BC = FL : (FL + Z),而我们将原来圆形的大小定为1单位,即BC = 1,那么DE = FL / (FL + Z)
在得到缩放比例后,那么对应的,图形在3D世界中的大小及坐标轴对应参数也可以轻易的得到,将圆图形的大小,x,y坐标均乘以缩放比例,就能得到在Z轴上运动时,物体此时的大小及位置参数(pos_为原图形参数)
x = pos_x * scale;
y = pos_y * scale;
size = pos_size * scale;
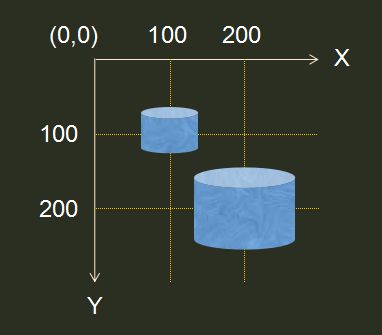
此时应该有同学发现一个问题,那就是canvas的起始坐标是在(0,0)位置上,那往Z轴正方向运动不就挪到屏幕外边去了?因此,为了方便理解,我们将原点挪到canvas中心上,也就是需要加上canvas长宽各一半
那么描述图形位置代码则变为(centerX = canvas.cilentWidth / 2,centerY同理,其实如果图形处于中心点,那么此图形实际只会有一个缩放效果,而不会有位置变化关系,有疑惑的同学可以自己演算一下就知道我说的什么了,上图如果白色圆形想变化出这四个位置,其实并不能在原点上,这里只是给同学们做一个图从视觉上联想一下结果):
x = pos_x * scale + centerX;
y = pos_y * scale + centerY;
上面这么一丢丢知识能干嘛?那就来个例子让大家可以用在应用里吧,一个很常见的粒子透视视觉
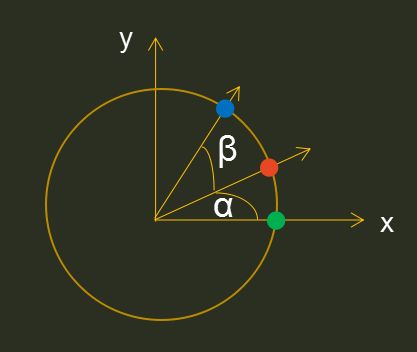
旋转后坐标计算:
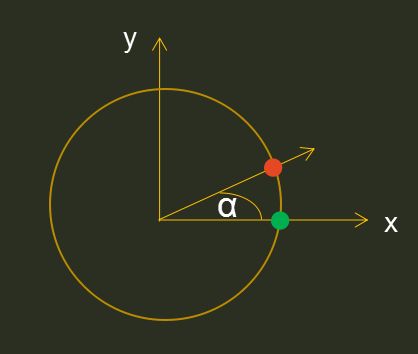
- 有过canvas2D开发经验的童鞋应该有学过如果计算旋转后坐标,旋转α度,则公式为:
x = r * cosα, y = r * sinα;
而在α角度基础上再旋转β度,则公式变成
x' = r * cos(α+β) , y' = r * sin(α+β)-
那么根据三角函数两角和差公式,则2转变为(这里的减加符号打不出来,只能截图,ppt里我是截图旋转图片,因为实在找不到这个符号):
将3代入2,可得:
x' = r * (cosαcosβ - sinαsinβ ), y' = r * (sinαcosβ + cosαsinβ)将1代入4,可得(结论,重点,高中知识忘记的现在也已经一步步重新推出来了,这是Z轴旋转计算公式):
x' = xcosβ - ysinβ, y' = ycosβ + xsinβ
上面就这么两个知识点能干哈?又得给出粒子demo来让大家学以致用了
回到我们最原始的需求上,因为需要完成平面图片的3D旋转视觉,所以需要获取图片的长宽,确定四个顶点位置,将顶点进行连接(lineTo)填充(fill),绘制成平面进行旋转,如果上面的知识你都学会了那这里比上面的demo复杂度还要低很多很多,直接上代码:
这里的关键代码是以下两部分:
上面要注意一点,我们将原点定在canvas中间,所以4个顶点在坐标上的表示(他们对应象限的正负符号)
以上代码是对上面两个知识点的应用,关于旋转与投影。
==================================================================
到这里,我们已经完成图片外形上的3D旋转视觉了,接下来只要把图片放进去,就大功告成,距离目标仅有一步之遥啦!
然而,现实总是这么残酷,下面的分享属于放弃系列,部分包含webgl的基础知识点,非战斗人员请尽快撤离
平面贴图实现思路:
现在我们来梳理一下思路:
- 加载图片,获取图片长宽,确定原始图片的四个顶点在当前canvas上的位置
- 将四个顶点绕Y轴旋转,并不停的重新计算四个顶点当前坐标,将其连接填充
- 根据观察,图形在旋转的时候多为梯形,那么我们需要将图形进行变形
- canvas api中,如果需要使用图片,需要用到drawImage()方法
CanvasRenderingContext2D.drawImage() 是 Canvas 2D API 中的方法,它提供了多种方式来在Canvas上绘制图像。
语法:
context.drawImage(image, x, y);
context.drawImage(image, x, y, width, height);
context.drawImage(img, sx, sy, swidth, sheight ,x, y, width, height);
参数 描述
img -- 规定要使用的图像、画布或视频。
sx -- 可选。开始剪切的 x 坐标位置。
sy -- 可选。开始剪切的 y 坐标位置。
swidth -- 可选。被剪切图像的宽度。
sheight -- 可选。被剪切图像的高度。
x -- 在画布上放置图像的 x 坐标位置。
y -- 在画布上放置图像的 y 坐标位置。
width -- 可选。要使用的图像的宽度。(伸展或缩小图像)
height -- 可选。要使用的图像的高度。(伸展或缩小图像)
而我们需要旋转图片,也就是需要用到该方法来进行图片绘制,那么此时将出现以下问题
drawImage()方法只能传入x, y及大小,而无法以4个顶点的方式传入绘制图片,而我们获取到的是四个投影后的顶点坐标。
那么我们来解决这一系列问题
- 图形旋转的时候,基本为梯形,那么此时我们需要将图形进行变形,也就是使用skew()来对图形进行变形,但我们得到的是顶点信息,而不是这个图形变形在xy轴上变化的角度有多少,所以我们需要使用的是canvas更加底层的方法 - 矩阵转换transform()方法。
但这里又引发了另外一个问题:矩阵转换只能做刚体变换(缩放、位移、旋转)及仿射变换(倾斜),这两种变换方式的特性是平行四边形变换后依然为平行四边形,无法实现投影变换(梯形) -
有稍微看过webgl知识的同学应该知道,任何图形都能通过点、线、面(三角片元)结合而成,例如我们上面的图形旋转,使用的就是点、线连接而成的结果,那么我们只需要应用webgl渲染原理思路,将图形切分为两个三角片元,再使用drawImage()方法,再使用一个clip()方法来进行裁切,就能完成投影变换
根据上图,每次都将两个矩阵转换后的图形重合,绿色不重合部分留上部分(或下部分),就能得到一个投影转换结果出来(ppt里不知道怎么对图形进行裁切,自行脑补吧,这里脑补量不大)
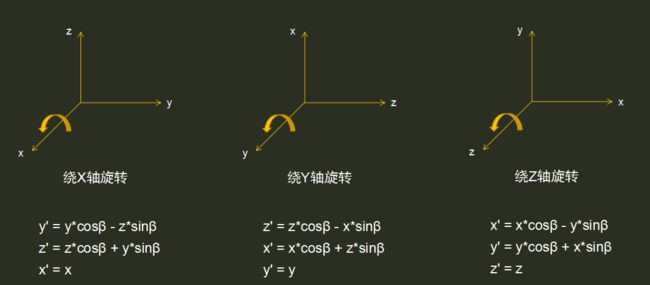
矩阵变换基础知识:
常用矩阵变换主要有以下四种,这里不对其原理进行解释,有兴趣的童鞋自行百度。
由于2d平面只有xy,所以跟webGL不同,这里是没有z轴的,所以呢,矩阵第三列并非z组成的矢量,而是对应webGL矩阵中的第四个分量,也叫常量项。
canvas 2d api中需要操作矩阵,需要使用transform方法
画布上的每个对象都拥有一个当前的变换矩阵。transform() 方法替换当前的变换矩阵。它会在前一个变换矩阵上构建。如果想要每一次操作都还原为初始矩阵(即transform(1,0,0,1,0,0)),需要使用setTransform()方法
语法:
context.transform(a,b,c,d,e,f);
参数 描述
a -- 水平缩放绘图
b -- 水平倾斜绘图
c -- 垂直倾斜绘图
d -- 垂直缩放绘图
e -- 水平移动绘图
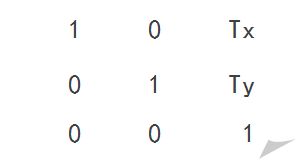
f -- 垂直移动绘图
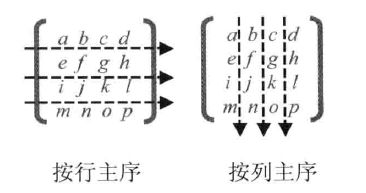
根据上图我们也知道了一件事,那就是transform()方法在数组中存储的矩阵元素是按列主序
这里对到有webGL基础的同学需要关注下,因为webGL中传递的矩阵元素是 按行主序的,只是我们可能会对齐为下面这种形式(比如下面这个旋转矩阵,对比一下上面的旋转矩阵图示,但它是个数组,所以传入顺序是 按行主序)
矩阵计算:
原坐标进行变化后,对应的矩阵计算请看下图,已经用颜色表明了应该哪个元素乘以哪个值
那么一个图形,如果先旋转再缩放,矩阵计算又该怎么算?请看下图,需要拆分成两步,先计算旋转矩阵乘以缩放矩阵,得到的矩阵再乘以原xy值
稍微说一下吧Ra、Rc、Re怎么来的吧,下面的Rb到Rf请自行演算,看结果是否与我图片上的一致
Ra = cosβ* Sx + (-sinβ) * 0 + 0 * 0 = cosβ * Sx
Rc = cosβ* 0 + (-sinβ) * Sy + 0 * 0 = -sinβ * Sy
Re = cosβ* 0 + (-sinβ) * 0 + 0 * 0 = 0
例子又来啦…看一下根据上面的知识,我们是否已经可以实现使用transform来实现api中的方法了呢?
reset
rotate
matrix旋转
rotate+scale
matrixMultiplication
matrixMultiplication3
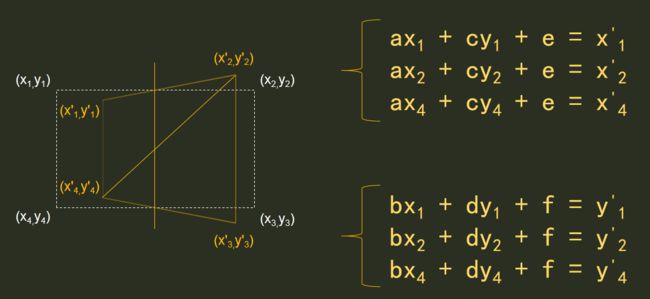
三元一次方程计算矩阵6个参数:
上面已经对矩阵转换的知识做好了铺垫,前面也已经实现了获取图形旋转时候的xy坐标,那么接下来就需要解决一个问题,我们应该如何将计算出来的旋转后xy坐标改变成可以传入矩阵当中的数值
先说一下思路吧,我们需要获取的矩阵变化当中的ace和bdf,初中知识也知道,要求三个未知数至少需要三个三元一次方程,而在我们对梯形切割成三角形后,三个顶点刚好满足三个参数,足以形成三个三元一次方程(如果这句话看着觉得难消化直接看图吧)
这里只对左上三角形写了六个三元一次方程,右下角的三角形可以自行画葫芦。来到这一步就完了吗?话说我们怎么解?
我们大多数人知道的解法就是消元,也就是先把其中一条方程改写成只含有一个未知数的方式,求解,然后计算剩下两个未知数。
来到这里,我们就会发现,如果用我们初中所学的顺序消元来计算的话将会特别繁琐(式子极长)。我们说到底就是要求矩阵的秩(ace、bdf),那么有一种特别符合要求的消元法就是用来解决这个问题的:高斯消元法
高斯消元法
我这里用这个词去网上查了一番,发现复制粘贴严重,都是同一套说法,相信数学基础不好的同学点开就要关闭了。所以我这里以结果倒推,让大家知道为了结果我们需要做什么
高斯消元,说到底就是要得到行阶梯形矩阵,我这里拿网上的图来说吧,以下图为例,(这里我忘记数学里叫啥了,反正就是未知数前面的系数)把系数拿出来,便可以获得一个增广矩阵(这部分的知识,所说的系数对应上面三角形位置对应三元一次方程.jpg,学完这部分将其代入我们就能得到矩阵的秩 -- ace、bdf)
// 三元一次方程组 //增广矩阵
2x + 3y + z = 11 2 3 1 11
x -2y + 3z = 6 => 1 -2 3 6
3x + 8y -2z = 13 3 8 -2 13
我们所需要做的就是将增广矩阵化简成下面的三角形式(数学基础较好的会知道这个不是最终标准型,但这里其实算到这里即可,后面的依旧使用代入法计算就行)
教学开始:就用上面的三元一次方程,用程序一步步来求解
/* step1 设定一组基础三元一次方程 */
let arr1 = [2, 3, 1, 11];
let arr2 = [1, -2, 3, 6];
let arr3 = [3, 8, -2, 13];
/* step2 数组排序,将方程的x值按照从大到小排序,因为我们看到上图最后一行的被消掉最多元的,这步操作也是为了减小放大系数 */
let originArr = [arr1, arr2, arr3];
// 重排,将三组三元一次方程按照未知数X的大小从大到小排列
originArr .sort(function (a, b) {
return b[0] - a[0];
})
/* step3 消除第二行 arr2 ,第三行 arr3 的 x 元 */
let [a1, a2, a3] = originArr;
let arr_2_f = a2[0];
let arr_3_f = a3[0];
for (let i = 0; i < 4; i++) {
a2[i] = a2[i] * a1[0] - a1[i] * arr_2_f;
a3[i] = a3[i] * a1[0] - a1[i] * arr_3_f;
}
/* step4 第三行 arr3 的 y 元 */
let arr_3_s = a3[1];
for (let i = 1; i < 4; i++) {
a3[i] = a3[i] * a2[1] - a2[i] * arr_3_s;
}
/* step5 计算出x, y, z的值 */
let z = a3[3] / a3[2];
let y = (a2[3] - z * a2[2]) / a2[1];
let x = (a1[3] - z * a1[2] - y * a1[1]) / a1[0];
console.log({x, y, z});
这里说一下为什么要用x和y的系数互相乘,而不是简单的除去最小公约数,因为会导致一个问题,那就是小数点,而彼此扩大对方系数倍数,这个值一定会是整数,用例子来说吧,比方下面两组数(随便乱写出来的),要消除第一行,我们可以第一行缩小4减去第二行即可,但是这个时候我们会计算出小数点的系数出来,那么就会增大误差,甚至出现无尽小数
4 3 6 13 => 1 0.75 1.5 3.25 // 小数点出来了,误差也随之而来
1 5 8 11
反之互相扩大对方x的系数
4 3 6 13 => 4 3 6 13 // 全部乘以1
1 5 8 11 => 4 20 32 44 // 全部乘以4
消除第二行x元,也就是上面的第一行减去第二行
0 -17 -26 -31 // 消元后依然能保持整数系数
完成高斯消元后,我们已经能将图片切分为两个三角形,使用transform和clip来进行图片旋转
这里的代码跟上面讲解的代码不一致,因为有关注这篇文章的人应该知道这篇文章被我晾了一整年了,不想重新实现,所以代码都是以前的,但是上面讲解的代码是我重新敲出来
旋转图片

通过上面的演示结果其实我们也可以看得出,由于矩阵转换加拼接的图片旋转,从视觉上一直总是一边大一边小,这也就是为什么全景里纹理贴图总能看出变形的原因,因为合并后的三角片元实际上并非同样的矩阵相乘结果(不明白这句话重新回去看一下上面那个绿色和橙色的梯形,两者实际上会得到两个不一致的矩阵,一个是大梯形一个是小梯形),而解决这个问题的方案就是想threejs一样,增加足够多的片元,那么转换出来的矩阵就会越接近,视觉上变形感知也会越小。因此最后一步就是将图片分解为足够多的三角片元
增加切割面获取多顶点位置
继续未完待续…最近没时间,就差一丢丢会写完的