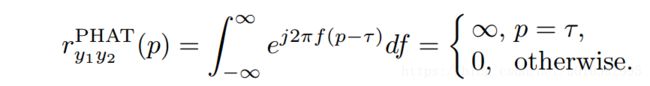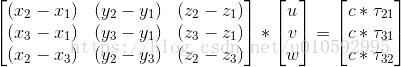麦克风阵列声源定位 GCC-PHAT
麦克风阵列声源定位(一)
利用麦克风阵列可以实现声源到达方向估计(direction-of-arrival (DOA) estimation),DOA估计的其中一种方法是计算到达不同阵元间的时间差,另外一种可以看这里,这篇主要介绍经典的GCC-PHAT方法
背景
简单说明问题背景,信号模型如下图,远场平面波,二元阵列
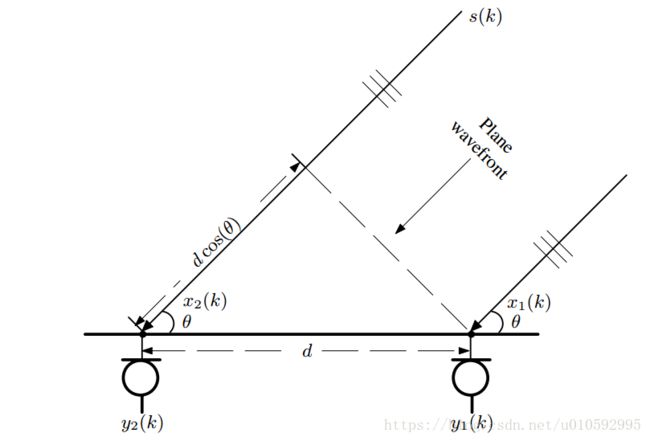
要计算得到 θ \theta θ,其实就是要求两个阵元接收到的信号时间差,现在问题变成到达时间差估计(Time-Difference-of-Arrival Estimation),因此,基于延时估计的DOA方法,其实也可以看做是分两步进行的,第一步是估计延时,第二步是计算角度,与之相对应的基于空间谱估计的DOA方法就是一步完成的。下面就分两步进行介绍
##1.延时估计
###1.1.互相关函数(cross-correlation function
计算 y 1 ( k ) y_1(k) y1(k)与 y 2 ( k ) y_2(k) y2(k)的时间差,可以计算两个信号的互相关函数,找到使互相关函数最大的值即是这两个信号的时间差
离散信号的互相关函数
R ( τ ) = E [ x 1 ( m ) x 2 ( m + τ ) ] R(\tau)=E[x_1(m)x_2(m+\tau)] R(τ)=E[x1(m)x2(m+τ)]
求时间差就是找到互相关函数最大时的点
D = a r g m a x R ( n ) D=argmaxR(n) D=argmaxR(n)
说的那么简单,那就用代码验证下
%%
% Load the chirp signal.
load chirp;
c = 340.0;
Fs = 44100;
%%
d = 0.25;
N = 2;
mic = phased.OmnidirectionalMicrophoneElement;
% array = phased.URA([N,N],[0.0724,0.0418],'Element',mic);
array = phased.ULA(N,d,'Element',mic);
%%
% Simulate the incoming signal using the |WidebandCollector| System
% object(TM).
arrivalAng = 42;
collector = phased.WidebandCollector('Sensor',array,'PropagationSpeed',c,...
'SampleRate',Fs,'ModulatedInput',false);
signal = collector(y,arrivalAng);
x1 = signal(:,1);
x2 = signal(:,2);
N =length(x2);
xc = xcorr(x1,x2,'biased');
[k,ind] = max(xc);
an = acos((ind-N)/Fs*340/d)*180/pi
xc12 = zeros(2*N-1,1);
m = 0;
for i = -(N-1):N-1
m = m+1;
for t = 1:N
if 0<(i+t)&&(i+t)<=N
xc12(m) = xc12(m) + x2(t)*x1(t+i);
end
end
end
xc12 = xc12/N;
以上程序中的循环就是上面的定义公式,运行程序可以看到循环部分计算的互相关与直接调用matlab的xcorr结果相同(注意matlab中互相关默认没做归一化),找到互相关函数的最大值就可以得到时间差
1.2.广义互相关(generalized cross-correlation)
理论上使用上面个介绍的CCF方法就可以得到时间差,但是实际的信号会有噪声,低信噪比会导致互相关函数的峰值不够明显,这会在找极值的时候造成误差。
为了得到具有更陡峭极值的互相关函数,一般在频域使用一个加权函数来白化输入信号,这就是经典的广义互相关方法。
由维纳-辛钦定理可知,随机信号的自相关函数和功率谱密度函数服从一对傅里叶变换的关系,即 x 1 、 x 2 x_1、x_2 x1、x2的互功率谱可由下式计算
P ( ω ) = ∫ − ∞ + ∞ R ( τ ) e − j ω τ d τ P(\omega)=\int_{-\infty }^{+\infty }R(\tau)e^{-j\omega\tau}d\tau P(ω)=∫−∞+∞R(τ)e−jωτdτ
R ( τ ) = ∫ − ∞ + ∞ P ( ω ) e j ω τ d ω R(\tau)=\int_{-\infty }^{+\infty }P(\omega)e^{j\omega\tau}d\omega R(τ)=∫−∞+∞P(ω)ejωτdω
这一步是把互相关函数变换到了频域,哦对,上面说到是想白化互相关函数,那就把上面第二式添加一个系数
R ~ ( τ ) = ∫ − ∞ + ∞ A ( ω ) P ( ω ) e j ω τ d ω \tilde{R}(\tau)=\int_{-\infty }^{+\infty }A(\omega)P(\omega)e^{j\omega\tau}d\omega R~(τ)=∫−∞+∞A(ω)P(ω)ejωτdω
设计不同的频域系数 A ( ω ) A(\omega) A(ω)对应着不同方法,这里只介绍 PHAT(phase transform)方法,即取系数如下:
A ( ω ) = 1 ∣ P ( ω ) ∣ A(\omega) = \frac{1}{\left | P(\omega) \right |} A(ω)=∣P(ω)∣1
基本思想就是求时间差只需要相位信息,舍弃不相关的幅度信息以提高健壮性,可以看到当 A ( ω ) = 1 A(\omega)=1 A(ω)=1的情况下就是经典互相关
P ( ω ) P(\omega) P(ω)为复数,可以表示为 ∣ P ( ω ) ∣ ∗ e − j ω p \left |P(\omega)\right |*e^{-j\omega p} ∣P(ω)∣∗e−jωp,去掉幅度信息后,就只剩相位信息 e − j ω p e^{-j\omega p} e−jωp了,要得到相位信息,可以用 P ( ω ) a b s ( P ( ω ) ) \frac{P(\omega)}{abs(P(\omega))} abs(P(ω))P(ω)计算,也可以直接用matlab中的angle函数计算,即 a n g l e ( P ( ω ) ) angle(P(\omega)) angle(P(ω)),
具体得到更陡峭的峰值的理论解释如下,详情参见《麦克风阵列信号处理》P198
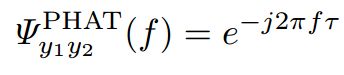
几行代码验证下:
x1 = [1,2,3,7,9,8,3,7]';
x2 = [4,5,6,5,4,3,8,2]';
[tau,R,lag] = gccphat(x1,x2)
N = length(x1)+length(x2)-1;
NFFT = 32;
P = (fft(x1,NFFT).*conj(fft(x2,NFFT)));
A = 1./abs(P);
R_est1 = fftshift(ifft(A.*P));
range = NFFT/2+1-(N-1)/2:NFFT/2+1+(N-1)/2;
R_est1 = R_est1(range);
R_est2 = fftshift(ifft(exp(1i*angle(P))));
R_est2 = R_est2(range);
可以看到,三种不同写法得到的R_est1 、R_est2 与matlab自带函数gccphat计算得到的R相等。
那上面例子中的宽带语音信号,用GCC-PHAT方法得到具有陡峭峰值互相关函数,找到互相关最大时的点,结合采样频率 F s 与 与 麦 克 风 间 距 d Fs与与麦克风间距d Fs与与麦克风间距d,就可以得到方向信息。频域计算互相关参考另一篇博客
##2.角度计算
上面的内容计算了两个麦克风的延时,实际中假设阵列中麦克风个数为 N N N,则所有麦克风间两两组合共有 N ( N − 1 ) / 2 N(N-1)/2 N(N−1)/2对,记第 k k k个麦克风坐标为 ( x k , y k , z k ) (x_k,y_k,z_k) (xk,yk,zk),声源单位平面波传播向量 u ⃗ = ( u , v , w ) \vec{u}=(u,v,w) u=(u,v,w),如果麦克风 k , j k,j k,j之间的延时为 τ k j \tau_{kj} τkj,则根据向量关系有下式,其中c为声速,
c ∗ τ k j = − ( x k ⃗ − x j ⃗ ) ∗ u ⃗ c*\tau_{kj} = -(\vec{x_k}-\vec{x_j})*\vec{u} c∗τkj=−(xk−xj)∗u
这样看起来不够直观,那就代入坐标写成标量形式如下:
c ∗ τ k j = u ∗ ( x k − x j ) + v ∗ ( y k − y j ) + w ∗ ( z k − z j ) c*\tau_{kj}=u*(x_k-x_j)+v*(y_k-y_j)+w*(z_k-z_j) c∗τkj=u∗(xk−xj)+v∗(yk−yj)+w∗(zk−zj)
当有多个麦克风时,每两个麦克风就可以得到一组上式, N 个 麦 克 风 就 会 有 N ∗ ( N − 1 ) / 2 个 等 式 N个麦克风就会有N*(N-1)/2个等式 N个麦克风就会有N∗(N−1)/2个等式,声源单位传播向量 u ⃗ = ( u , v , w ) \vec{u}=(u,v,w) u=(u,v,w) 有三个未知数,因此最少只需要三组等式,也就是三个麦克风就可以计算出声源方向,这里就先假定 N = 3 N=3 N=3,可以得到方程组如下:
c ∗ τ 21 = u ∗ ( x 2 − x 1 ) + v ∗ ( y 2 − y 1 ) + w ∗ ( z 2 − z 1 ) c*\tau_{21}=u*(x_2-x_1)+v*(y_2-y_1)+w*(z_2-z_1) c∗τ21=u∗(x2−x1)+v∗(y2−y1)+w∗(z2−z1)
c ∗ τ 31 = u ∗ ( x 3 − x 1 ) + v ∗ ( y 3 − y 1 ) + w ∗ ( z 3 − z 1 ) c*\tau_{31}=u*(x_3-x_1)+v*(y_3-y_1)+w*(z_3-z_1) c∗τ31=u∗(x3−x1)+v∗(y3−y1)+w∗(z3−z1)
c ∗ τ 23 = u ∗ ( x 2 − x 3 ) + v ∗ ( y 2 − y 3 ) + w ∗ ( z 2 − z 3 ) c*\tau_{23}=u*(x_2-x_3)+v*(y_2-y_3)+w*(z_2-z_3) c∗τ23=u∗(x2−x3)+v∗(y2−y3)+w∗(z2−z3)
写成矩阵形式
求出 u ⃗ = ( u , v , w ) \vec{u}=(u,v,w) u=(u,v,w) 后,由正余弦关系就有了角度值了
θ = a c o s ( 1 w ) \theta=acos(\frac{1}{w}) θ=acos(w1)
α = a c o s ( u s i n ( a c o s ( 1 w ) ) ) \alpha=acos(\frac{u}{sin(acos(\frac{1}{w}))}) α=acos(sin(acos(w1))u)
当麦克风数量 N > 3 N>3 N>3时,其实所有组合信息对于角度值的计算是有冗余的,这个时候可以求出所有组合的角度值,然后利用最小二乘求出最优解,这样可以利用到所有的麦克风的信息来提高角度估计的稳定性
References:
- J. Benesty, J. Chen, and Y. Huang, Microphone Array Signal Processing. Berlin, Germany: Springer-Verlag, 2008.
- J. Dibiase. A High-Accuracy, Low-Latency Technique for Talker Localization in Reverberent Environments using Microphone Arrays. PhD thesis, Brown University, Providence, RI, May 2000.
- J.-M. Valin, F. Michaud, J. Rouat, D. Letourneau, Robust Sound Source Localization Using a Microphone Array on a Mobile Robot. Proc. IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), pp. 1228-1233, 2003.