稀疏矩阵的存储格式
题注:看到网上有这方面的东西,但是不多,映像当中,中文的版本只有一个,讲解不够清楚,而且还有错误的地方,在经过查阅资料之后将存储格式中最为重要也是中文版本中的所有重新进行说明,以期望对大家有所帮助吧!分割区中的部分为本人改造版本,其余引用自他人:稀疏矩阵的存储格式(Sparse Matrix Storage Formats)Sason
对于稀疏矩阵,仅仅存储非零元素可是矩阵操作效率更高。现有很多种稀疏矩阵的存储方式,但是多数采用相同的基本技术,即存储矩阵所有的非零元素到一个线性数组中,并提供辅助数组来描述元数组中非零元素的位置。
以下是几种常见的稀疏矩阵存储格式:
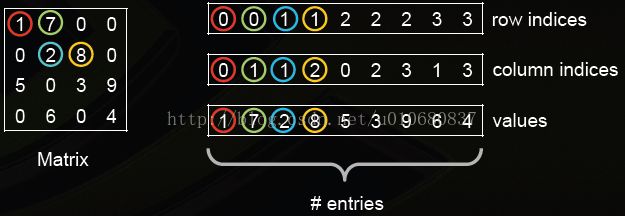
1.Coordinate Format(COO)
这种存储方式的主要优点是灵活、简单。仅存储非零元素以及每个非零元素的坐标。
使用3个数组进行存储:values, rows, and column indices
- values: 实数或复数数据,包括矩阵中的非零元素, 顺序任意。
- rows: 数据所处的行 。 columns indices: 数据所处的列。
--------------------------------------------------------------------分割区开始----------------------------------------------
2.Diagonal Storage Format(DIA)
首先,左边的矩阵的主对角线是<1234>,在右边的矩阵中发现第二列就是<1234>,如果在左边的矩阵中,将主对角线向右上角移动一个单位,则变成了<789>,在右边的矩阵中可以看到第三列是<798*>,下来解释一下为什么是<798*>,而不是<*789>,注意到左边的矩阵中,7是位于最上方的,这就是原因,然后来看,在左边矩阵中,主对角线向左下角移动两个单位,就会有<5,6>出现,根据以上的解释,当然在右边的压缩矩阵中,就会出现<**56>.以上右边的矩阵我们成为values;
我们还需要一个向量来表示values中每一列对应原矩阵中主对角线的什么位置上,此向量我们称为distance,如果位于主对角线上,distance[i]=0,如<789>,那它的distance[i] = 1 ,<56>,它的distance[i] = -2。
3.Compressed Sparse Row Format(CSR)
****这个format ,nice !
values and column indices 的意思十分明白,不解释,row offsets需要解释一下,row offsets[0 2 4 7 9],其中要是写成这样看会如何呢,values[0, 2 4 7 9],(当然是没有values[9]),那values[0] is 1, values[2] is 2, values[4] is 5, values[7] is 6, values[9] is out of index. row offsets 的作用是记录values中的值位于原矩阵中哪个行的作用,有行的索引,有column indices 就可以满足了。
###CSC基本和上面的类似,只不过是将左边的按照列优先算的。
6.Block Compressed Sparse Row Format(BSR)
这个很简单,链接在此,一看便会了。
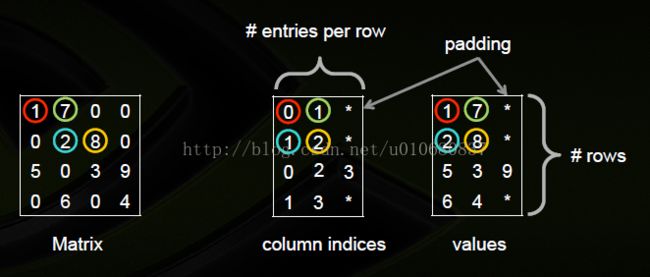
7.ELLPACK(ELL)
网上汉文中的版本就是这张图错误,致使很多人没能将这张解释清楚。修正后的版本很容易弄懂,就不多言了。
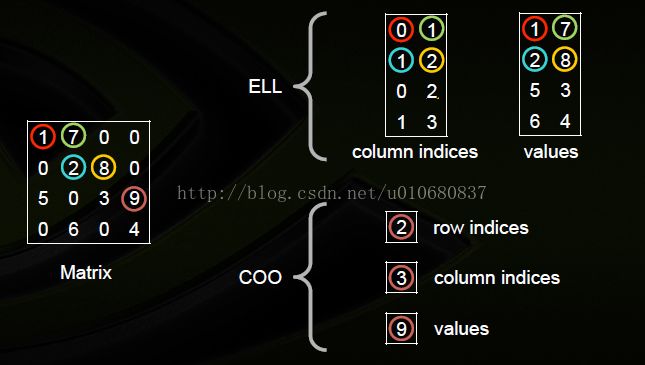
8.Hybrid(HYB)
这张图也是修正后的版本,原因也是由于ELL错误造成的。
该格式就是ELL+COO两种格式结合而成。
这些应用的实例在python的scipy包中有实现,详细应用查看,请点击
----------------------------------------------------------------分割区尾--------------------------------------------------------------
选择稀疏矩阵存储格式的一些经验:
1. DIA和ELL格式在进行稀疏矩阵-矢量乘积(sparse matrix-vector products)时效率最高,所以它们是应用迭代法(如共轭梯度法)解稀疏线性系统最快的格式;
2. COO和CSR格式比起DIA和ELL来,更加灵活,易于操作;
3. ELL的优点是快速,而COO优点是灵活,二者结合后的HYB格式是一种不错的稀疏矩阵表示格式;
4. 根据Nathan Bell的工作,CSR格式在存储稀疏矩阵时非零元素平均使用的字节数(Bytes per Nonzero Entry)最为稳定(float类型约为8.5,double类型约为12.5),而DIA格式存储数据的非零元素平均使用的字节数与矩阵类型有较大关系,适合于StructuredMesh结构的稀疏矩阵(float类型约为4.05,double类型约为8.10),对于Unstructured Mesh以及Random Matrix,DIA格式使用的字节数是CSR格式的十几倍;
5. 从我使用过的一些线性代数计算库来说,COO格式常用于从文件中进行稀疏矩阵的读写,如matrix market即采用COO格式,而CSR格式常用于读入数据后进行稀疏矩阵计算。
参考:
稀疏矩阵的存储格式(Sparse Matrix Storage Formats)
Sparse Matrix Representations & Iterative Solvers Lesson 1 --- Nathan Bell [nvida]
Sparse Matrix-Vector Multiplications on Graphics Processors Mhd. Amer Wafai [Master Thesis Nr.2938]
ELL_Matrix Class