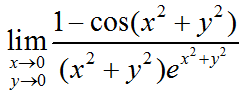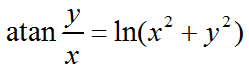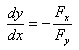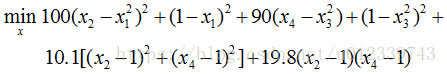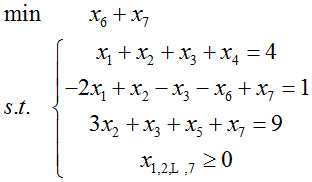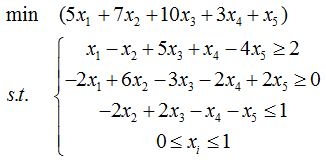Matlab在科学计算中的应用（学习笔记）

MATLAB和Mathematica、Maple并称为三大数学软件。它在数学类科技应用软件中在数值计算方面首屈一指。MATLAB可以进行矩阵运算、绘制函数和数据、实现算法、创建用户界面、连接其他编程语言的程序等，主要应用于工程计算、控制设计、信号处理与通讯、图像处理、信号检测、金融建模设计与分析等领域。

---

目录

---

MATLAB1

varargin（可变输入参数个数）

编写一个矩阵相加函数mat_add() ，使其具体的调用格式为A=mat_add(A1 ,A2 ,A3 ,…) ， 要求该函数能接受任意多个矩阵进行加法运算。（注：varargin 变量的应用）

function A = mat_add(varargin)
    try,A = 0;
        for i = 1:length(varargin),A = A + varargin{i};end
    catch,error(lasterr);end
end

limit（求极限）

试求出如下极限。

syms x y;
fc=(1-cos(x^2+y^2))*exp(x^2+y^2)/(x^2+y^2);
limit(limit(fc,x,0),y,0)

diff（求导数）

试求出下面函数的导数。

syms x y; 
f=atan(y/x)-log(x^2+y^2);
f1=simplify(-diff(f,x)/diff(f,y))

注：隐函数导数公式

int（积分）

syms x y t
f=int(exp(-t^2),t,0,x*y);
x/y*diff(f,x,2)-2*diff(diff(f,x),y)+diff(f,y,2)
simplify(ans)

taylor（幂级数）

试求出下面函数的Taylor幂级数展开。

syms x a; 
f=exp(-5*x)*sin(3*x+sym(pi)/3);
taylor(f,x,a,'Order',4)

注：这里展开前4项。

symsum（递推式求和）

试求出下面的极限。

syms k n;
limit(n*symsum(1/(n^2+k*pi),k,1,n),n,inf)

quadgk@（二重积分与匿名函数）

计算被积函数

在[0,1）区间上的积分。

f = (@(x)exp(x).*log(x));
q = quadgk(f,0,1)

integral3（三重积分）

f = @(x,y,z) y.*sin(x)+z.*cos(x);
q = integral3(f,0,pi,0,1,-1,1)

MATLAB2

solve（解方程，vpa精确度）

求解下面的联立方程，并检验得出的高精度数值解（准解析解）的精度。

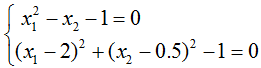
syms x1 x2;
[r1,r2]=solve(x1^2-x2-1==0,(x1-2)^2+(x2-0.5)^2-1==0);
vpa(r1),vpa(r2)

Jacobi、Gauss-Seidel（迭代法求解方程组）

用Jacobi、Gauss-Seidel迭代法求解方程组

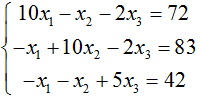
给定初值为

Jacobi迭代法

% jacobi.m
function y=jacobi(a,b,x0)
D=diag(diag(a));  U=-triu(a,1); L=-tril(a,-1);
B=D\(L+U);   f=D\b;
y=B*x0+f;
n=1;
while norm(y-x0)>=1.0e-6
    x0=y;
    y=B*x0+f;
    n=n+1;
end
n

>> a=[10,-1,-2;-1,10,-2;-1,-1,5];b=[72;83;42];
>> jacobi(a,b,[0;0;0])

Gauss-Seidel迭代法

% gauss_seidel.m
function y=gauss_seidel(a,b,x0)
D=diag(diag(a));U=-triu(a,1);L=-tril(a,-1);
G=(D-L)\U  ;f=(D-L)\b;
y=G*x0+f;  n=1;
while norm(y-x0)>=1.0e-6
    x0=y;
    y=G*x0+f;
    n=n+1;
end
n

>> a=[10,-1,-2;-1,10,-2;-1,-1,5];b=[72;83;42];
>> gauss_seidel(a,b,[0;0;0])

MATLAB3

fminunc（无约束最优化）

试求解下面的无约束最优化问题。

 f=inline(['100*(x(2)-x(1)^2)^2+(1-x(1))^2+',...
'90*(x(4)-x(3)^2)+(1-x(3)^2)^2+',...
'10.1*((x(2)-1)^2+(x(4)-1)^2)+',...
'19.8*(x(2)-1)*(x(4)-1)'],'x');
x=fminunc(f,ones(4,1))

linprog（线性规划）

试求解此线性规划问题：

f=[0,0,0,0,0,1,1];
Aeq=[1 1 1 1 0 0 0; -2 1 -1 0 0 -1 1; 0 3 1 0 1 0 1];
Beq=[4; 1; 9]; xm=[0;0;0;0;0;0;0]; A=[]; B=[];
x=linprog(f,A,B,Aeq,Beq,xm)

fmincon（线性规划）

试求解下面的非线性规划问题。

% exc6fun6.m
% 可以用下面的语句描述目标函数
function y=exc6fun6(x)
    y=exp(x(1))*(4*x(1)^2+2*x(2)^2+4*x(1)*x(2)+2*x(2)+1);
end

% exc6fun6a.m
% 也可以写出约束函数
function [c,ce]=exc6fun6a(x)
    ce=[];
    c=[x(1)+x(2); x(1)*x(2)-x(1)-x(2)+1.5; -10-x(1)*x(2)];
end

A=[]; B=[]; Aeq=[]; Beq=[]; xm=[-10; -10]; xM=[10; 10];
x0=(xm+xM)/2;
ff=optimset; ff.TolX=1e-10; ff.TolFun=1e-20;
x=fmincon('exc6fun6',x0,A,B,Aeq,Beq,xm,xM,'exc6fun6a',ff)
% i=1; x=x0;
% while (1)
%     [x,a,b]=fmincon('exc6fun6',x,A,B,Aeq,Beq,xm,xM,'exc6fun6a',ff);
%     if b>0, break; end
%     i=i+1;
% end
% x,i % 循环次数为5

注：这里本来想将上面两个函数写为匿名函数。结果跑结果出错了。

bintprog（0-1规划）

试求解0－1线性规划问题。

% 下面的语句利用MATLAB 7.0 提供的新函数
f=[5 7 10 3 5]; B=[-2; 0; 1];
A=[-1 1 -5 -1 4; 2 -6 3 2 -2; 0 -2 2 -1 -1];
x=bintprog(f,A,B,[],[])'

MATLAB4

normfit（置信区间）

某研究者对随机抽取的一组保险丝进行了实验，测出使保险丝烧断的电流值为10.4, 10.2,12.0, 11.3, 10.7, 10.6, 10.9, 10.8, 10.2, 12.1，假设这些值满足正态分布，试在置信水平 的条件下求出这些保险丝的溶断电流及其置信区间。

x=[10.4,10.2,12,11.3,10.7,10.6,10.9,10.8,10.2,12.1];
[m1,s1,ma,sa]=normfit(x,0.05); ma

jbtest检验

假设测出某随机变量的12 个样本为9.78, 9.17, 10.06, 10.14, 9.43, 10.60, 10.59, 9.98, 10.16,10.09, 9.91, 10.36，试求其方差及方差的置信区间。

% 先假设该随机变量满足正态分布，则可以用下面的语句进行检验
% h为测试结果,若h=0,则可以认为X是服从正态分布的;若h=1,则可以否定X服从正态分布
x=[9.78,9.17,10.06,10.14,9.43,10.6,10.59,9.98,10.16,10.09,9.91,10.36];
[H,p,c,d]=jbtest(x,0.05); H
% 经确认满足正态分布，所以用normfit() 函数即可以求出方差及方差的置信区间
[m1,s1,ma,sa]=normfit(x,0.05); s1,sa

References:
[1] 张敏洪老师的《Matlab在科学计算中的应用》PPT以及课后作业题
[2] 百度百科，MATLAB，https://baike.baidu.com/item/MATLAB，2018-5-22

©qingdujun
2018-5-22 于北京 怀柔