【GAN ZOO】Precomputed Realtime Texture Synthesis with Markovian Generative Adversarial 用MGAN预训练实时纹理合成
原文地址 https://link.springer.com/chapter/10.1007/978-3-319-46487-9_43
补充材料和代码 https://github.com/chuanli11/MGANs。
摘要
本文提出了马尔可夫生成对抗网络(MGANs),一种用于训练有效纹理合成的生成神经网络的方法。尽管深度神经网络方法最近在合成质量方面表现出显著的结果,但它们仍然具有相当大的计算成本(低分辨率图像的运行时间)。作者的论文解决这个效率问题。与之前工作中的数值反卷积不同,作者预先计算了一个前馈跨步卷积网络,该网络捕捉马尔可夫块的特征统计量,并能够直接生成任意维度的输出。这种网络可以直接将棕色噪声解码为逼真的纹理细节,或者将照片直接解码为艺术画。通过对抗训练,作者获得的图像质量可与近期的神经纹理合成方法相媲美。由于生成时不再需要优化,因此本文方法运行时的性能(25MHz下的0.25M像素图像)显著优于先前的神经纹理合成器(速度提高至少500倍)。作者将这个想法应用于纹理合成,样式转换和视频风格化。
关键词: Texture synthesis, Adversarial Generative Networks
1、引言
图像合成是计算机图形学和视觉中的一个经典问题[6,33]。关键的挑战是以简明,可学习的模式捕捉复杂类别图像的结构,并找出用于学习这些模型和合成新图像数据的高效算法。大多数传统的“纹理合成”方法使用马尔科夫随机场(MRF)模型来解决复杂性约束,该模型通过局部像素块的统计来表征图像。
最近,基于深度神经网络的生成模型已经展示了图像合成的新视角[10,8,11]。深度结构可以捕捉对象类中的外观变化,并具有超像素级的能力。但是,从有限的训练数据中可以学到多少结构还有很大的局限性。目前,有两类主要的“深层”生成模型:1)生成完整图像的全图像模型[10,3];2)合成纹理的马尔可夫模型[8,21]。
第一类的全图像模型通常被设计为经过特殊训练的自动编码器[16,11]。结果令人印象深刻,但局限于相当小的图像(通常约64×64像素),细节保真度有限。第二类是深度马尔可夫模型,仅捕获局部块的统计信息,并将它们组装成高分辨率图像。因此,细节的保真度是好的,但如果应该重现非平凡的整体结构,则需要额外的指导[6,12,1,8,21]。本论文讨论了第二种深度马尔可夫纹理合成的方法。
以前的这种类型的神经方法[8,21]建立在去卷积框架之上[37,25]。这很自然地提供了块和复杂的复用的混合,允许重用像VGG网络[30]这样的大型,受过判别训练的神经网络的错综复杂的多层次特征表示,并将它们重新用于图像合成。稍后会提到这个方面,这对高质量结果是非常重要的(图10)。 Gatys等人[8]通过用更高级的特征向量的全局高斯模型建模块统计来开创这种方法,并且Li等人[ [21]利用扩展的局部神经激活块字典,视觉现实主义的折衷灵活性。
深马尔可夫模型能够产生显着的视觉效果,远远超过传统的像素级MRF方法。不幸的是,反卷积方法的运行时成本仍然非常高,需要迭代反向传播以估计特征激活(更高网络层)的pre-image(像素)。在对高级功能修补程序的MRF进行建模的最昂贵的情况下,高端GPU需要几分钟才能合成低分辨率图像(例如512×512像素图像)。
因此,作者的论文的目的是提高深马尔可夫纹理合成的效率。关键的想法是通过将一个跨越式卷积网络[31,29]应用于反演过程来预先计算网络的反演,该反演过程纯粹以前馈方式进行。尽管接受了固定大小的块的训练,但生成的网络可以生成任意维度的连续图像,而无需任何额外的优化或混合,从而生成具有特定风格和高性能的高质量纹理合成器2。
作者使用对抗训练来训练卷积网络[29],它可以保持图像质量,类似于原始的昂贵的优化方法。因此,作者获得了显着的提速:作者的GPU实现在40ms内(在nVidia TitanX上)计算512 512个图像。关键的限制当然是为每种纹理风格预先计算前馈卷积网络。尽管如此,对于许多潜在的应用来说,这仍然是一个有吸引力的交换,例如来自艺术形象或视频风格的领域。作者在实验中探索一些这些应用。
2、相关工作
反卷积网络已经被用于可视化深层特征和对象类。Zeiler等[37]在像素级别反向投影神经激活函数。Mahendran等[ 23 ]从中间层中的神经编码重构图像。近来的努力都是为了提高效率,并提高可视化的准确性[ 26,36 ]。Mordvintsev等显示了反卷积类特定激活函数如何从网络中创造能够以假乱真的图像[18 ]。这项工作得到了广泛的认同。获得可视模式方法的复杂度很高,因此已经刺激了一些新的生成模型的出现:Gatys等[ 8,7 ]提出通过全局统计高层神经网络特征向量的协方差,在艺术特征变换上得到了很好的效果。统计模型有一些局限性:强迫去统计每一个特征向量,会生成一些从没有在实际数据中出现过的特征模式组合,这使得学习得到的纹理有一些不合理。这可以通过块特征来代替点特征的方式局部解决 [21 ]。在某些情况下这种方法可以有照片般逼真的合成,但这种方法同时也降低了模型的不变性,因为简单的像素块字典通常是确定的。在理论方面,谢等人[34]提出生成随机域模型可以从判别神经网络中导出,并且在无监督的纹理合成上有所运用。
完整图像方法采用受过专门训练的自动编码器作为生成网络[ 16 ]。例如,生成对抗网络使用两个网络:一个作为判别器,另一个作为生成器,通过玩极大极小游戏以迭代地改进模型[10 ]。该模型被扩展为一个拉普拉斯金字塔[ 9 ]。Radford等[ 29 ]提出了一套架构精炼方法[ 29 ]以稳定该模型的性能,并表明,该生成器具有矢量算术性质。对抗网络的一个重要优势在于它提供感知度量指标[ 20, 4 ],允许自动编码器更有效地训练。这些模型也可以通过语义赋值[ 35 ]、图像说明[ 24 ]、三维数据[ 5, 17 ]、时间/空间状态[ 11, 13, 27 ]等方法来增强。
Ulyanov等[ 32 ]和Johnson等[ 14 ]提出了Gatys方法的快速实现。他们的方法采用与质感损失来训练预计算解码器,并在运行时获得了显著增益(高解码器复杂度降低了他们的速度)。本论文的主要区别是采用Li [21 ] 所提出的方法,使用特征块统计数据,以此能够更真实的再现一些纹理分布。
3、模型
首先在概念上阐述本文方法的动机。基于统计的方法[ 8,32 ]利用高斯模型将图匹配源的分布(输入相片或噪声信号)和目标(纹理)的分布相匹配(如图 1 的第一个图所示)。然而,现实世界的数据并不总是符合高斯分布。相反,它们往往对应于一个复杂的非线性流形。对抗性训练[ 10 ]可以通过判别网络识别这样的流形(图 1 的第二个),并通过投影加强其生成能力(图 1 的第三个)。作者在与内容对应的马尔可夫像素块适用对抗性训练(图 1 的第四个),这样学习可以专注于相同语境下的上下文的描绘,而不是上下文混合与不同描绘之间的映射。

图1 Motivation:现实世界的数据并不总是符合高斯分布(第一个图),而是一个复杂的非线性流形(第二个图)。作者通过对抗学习,得到图像投影到那个流形的的上下文相关像素块。
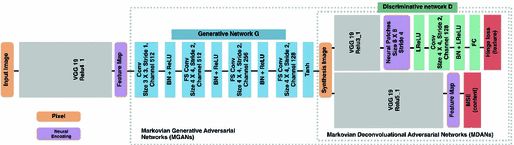
图2 本文的模型包含生成网络(蓝块)和判别网络(绿块)。
作者应用马尔可夫像素块判别训练(紫色块作为判别网络的输入)。
图 2 可视化本文的流程,它扩展了李的基于块拼贴的合成算法[ 21 ]。作者先更换了补丁字典(包括迭代最近邻搜索)用连续判别网络 D D D(绿块)学习区分不适当合成的像素块与真实的像素块(在VGG_19和Relu3_1上,紫块)。用VGG_19编码相同图像的第二比较层(下面的流程 D D D ),Relu5_1可以被选择用于指导。如果在VGG网络上(用梯度从判别器和可选地从引导内容)运行去卷积,将得到解卷积图像合成器,作者称之为马尔可夫解卷积对抗性网络(MDANs)。
MDANs是很慢的。因此,作者目标是额外生成网络 G G G(蓝色块)。它通过VGG_19层Relu4_1将图像直接解码为所需要的合成图像。在训练过程中,作者不改变VGG_19网络(灰色块),只优化 D D D 和 G G G 。作者将整个架构称为马尔可夫生成对抗网络(MGANs)。
3.1 马尔可夫解卷积对抗性网络(MDANs)
MDANs的纹理合成是由对抗训练驱动的解卷积过程:一个判别网络 D D D (在图2中的绿色块)被训练去区分合成图像与实例图像,并在relu3_1和VGG_19使用规则采样进行输出(紫色块)。它输出每个像素块的的分类评分 s = ± 1 s= ± 1 s=±1 ,表示该像素块的真实程度( s = 1 s= 1 s=1 是真的)。从合成图像采样的每个像素块, 1 − s 1 - s 1−s 是它要最小化的语义损失。去卷积处理逐像素反向传播这,一损失像Radford等[ 20 ]的方法一样,作者使用批标准化和leaky ReLU来优化训练 D D D 。
从形式上说,作者将具有某种结构的图像记为 x t ∈ R ω t × h t x_t\in\mathbb R^{\omega_t×h_t} xt∈Rωt×ht,将合成图像记为 x ∈ R ω × h x\in\mathbb R^{\omega×h} x∈Rω×h 。作者通过随机噪声初始化无指导的合成图像 x x x ,或者在某些有监督的情况下,用某些有内容的图像 x c ∈ R ω × h x_c\in\mathbb R^{\omega ×h} xc∈Rω×h 来初始化。去卷积过程迭代进行,以最小化以下的能量:
(1) x = arg min x E t ( Φ ( x ) , Φ ( x t ) ) + α 1 E c ( Φ ( x ) , Φ ( x c ) ) + α a Υ ( x ) x=\arg\min_x E_t(\Phi(x),\Phi(x_t))+\alpha_1E_c(\Phi(x),\Phi(x_c))+\alpha_aΥ(x)\tag{1} x=argxminEt(Φ(x),Φ(xt))+α1Ec(Φ(x),Φ(xc))+αaΥ(x)(1)
E t E_t Et 用于指代结构上的损失,其中 Φ ( x ) \Phi(x) Φ(x) 是VGG_19经过relu3_1输出的特征图。作者从 Φ ( x ) \Phi(x) Φ(x) 中采样像素块,并且用Hinge Loss计算他们标签的损失:
(2) E t ( Φ ( x ) , Φ ( x t ) ) = 1 N ∑ i = 1 N max ( 0 , 1 − s i ) E_t(\Phi(x),\Phi(x_t))=\frac 1 N\sum_{i=1}^N\max(0,1-s_i)\tag{2} Et(Φ(x),Φ(xt))=N1i=1∑Nmax(0,1−si)(2)
s i s_i si 表示第 i i i 个神经块的分类分数, N N N 是 Φ ( x ) \Phi(x) Φ(x) 全部采样块的数目。判别网络是这样被训练的:他们的参数被随机初始化,然后在每一次去卷积之后被更新,然后在合成图像的结果上越来越好。
公式(1)中的额外的正则化器 Υ ( x ) Υ(x) Υ(x) 是像素的一个平滑先验[23],使用 E t E_t Et 和 Υ ( x ) Υ(x) Υ(x) 可以使得随机的纹理变得有结构(如图3)。通过最小化加性内容损失 E c E_c Ec ,神经网络可以生成语义上与引导图像 x c x_c xc 相关的图像(如图4)。这种内容损失是两个特征图 Φ ( x ) \Phi(x) Φ(x) 与 Φ ( x c ) \Phi(x_c) Φ(xc) 之间的均方误差。作者将权值设定为 α 1 = 1 \alpha_1=1 α1=1 , α 2 = 0.0001 \alpha_2=0.0001 α2=0.0001 ,使用ADAM优化(学习率0.02,momentum设置为0.5)去最小化公式1。要注意每一个神经块都通过反向传播得到关于 D D D 的导数。为了在相邻的块中有一致的传播,作者使用texture optimization[18]中的方法优化梯度的输出。

图3 使用MDANs在未经引导情况下的纹理合成。对于每一个情况中,第一图像是样例的结构,另两个是合成的结果。图片来源:[ 34 ]的‘常春藤’,Flickr用户erwin brevis的“gell”,葛饰北斋的‘神奈川冲浪里’,Kandinsky的‘作品七号’。
3.2 马尔科夫生成对抗网络(MGANs)
MDANs需要多次迭代和每个输出图像独立运行。作者训练一个变分自动编码器(VAE),将特征图直接映射到解码像素。目标的例子(纹理照片)从MDANs获得。生成器 G G G 以VGG_19经过Relu4_1激活的结果作为输入,然后通过一个普通的卷积,然后经过fractional-strided卷积(FS CONV)对图片进行解码。尽管生成器是按照具有固定大小的输入被训练的,它可以自然延伸到任意尺寸的图像。
如Dosovitskiy [ 4 ] 所指出的,找到一个很好用于训练自动编码器的度量是极为重要的:使用合成图像与像素级的目标图像之间的欧几里德距离(图 5,像素变分自动编码器)产生过度平滑的图像。在神经编码级别比较可以改进结果(图 5,神经变分自动编码器)对抗性训练能够进一步提高生成结果的质量(图 5,MGANs)。
本文的做法是类似于经典生成对抗性网络(GANs)[ 10 ],最关键的区别是不在整张图像上进行操作,而是从相同图像中得到的很多像素块。这样利用块之间的上下文的对应关系,使得学习目标类分布[10 ]或内容不相关的数据之间的映射[22]变得更容易更有效。另外还将Sigmoid和二进制交叉熵准则 [29 ] 更换为max margin标准(Hinge loss)。这避免了 D D D 的消失梯度问题。这比Radfort的情况更困难[29],因为训练数据有较少多样性。因此,Sigmoid函数可以容易地饱和。
图 5(MGANs)显示了制作毕加索的“自画像1907年”的风格画网络的结果。在训练过程中,作者随机从CelebA数据选择了75张人脸的照片[22 ],并额外从公开数据中选择了25张非名人照片。在实验中,作者调整所有的照片的最大尺寸为384个像素。作者通过旋转和尺度变换将每张图片重复九倍,以进行数据增强。作者通过128-128 croppings定期抽样子窗口以进行批处理。共有24506个训练示例,每一个被看作从relu3_1层采样的神经块作为 D D D 的输入。

图5 使用MGANs学习从VGG_19编码的样式照片。参考纹理是利用MDANs学习的毕加索“自画像1907”。作者在训练和测试数据比较MGANs、Pixel VAE和Neural VAE的结果。

图6 MGANs的训练期间的中间解码结果。MDANs的参考样式纹理是毕加索的“自画像1907年”。
图 5(顶行,MGANs)显示本文的生成网络用于训练照片的解码结果。底行显示了网络概括很好地测试数据。值得注意的是,用于测试图像的MDANs图像从未在训练中使用。然而,用 G G G 直接解码产生的非常好的近似。MDANs和MGANs之间的主要区别是:MDANs更好的保存输入图像的内容,MGANs生成的是有一种风格的结果。这是因为MGANs用许多图像的训练,因此学到的最频繁的特征。另一个明显的区别是MDANs创造更多的天然背景(如带平面的着色区域),由于它的迭代优化训练。尽管有这样的缺陷,该MGANs模型产生具有速度快2500倍,并且效果相当的结果。
图 6 显示了一些MGANs的中间结果。很显然,训练越多,解码器效果更好。100个批次后,网络能够学习整体颜色,能够得到有强烈反差的区域。经过300个批次的网络开始产生纹理。经过1000个批次,就会学到如何画眼睛。进一步的培训能够删除一些幻影伪像的结果。模型所生成的结果相对于测试数据测试数据(右边)效果不错。
4、实验分析
作者通过研究一些超参数(层分类,块大小)和模型的复杂性(在网络中的层数,每层中的通道的数量)。虽然有可能不适合所有纹理通用优化设计,作者的研究揭示模型一般的行为的一些情况。为公平的比较,在本研究的例子纹理被固定到128×128像素,合成输出被固定到256×256个像素。
可视化解码器的特点: 作者在图 7 可视化了学习到的解码器 G G G 。这些特征被直接从one-hot输入矢量解码。单个修补程序类似但不是很忠实地匹配示例的纹理(由于编码的半分布式和非线性)。然而,相似性强大到足以合成新的图像。

图7 可视化的生成网络学习过程。图片来源:[ 34 ]的‘常春藤’,Flickr用户erwin brevis的“gell”,Katsushika Hokusai的‘神奈川冲浪里’。
**参数:**在这里,我们尝试不同的输入层的判别网络。要做到这一点,作者运行没有指导的纹理合成与判别器 D D D ,取VGG_19的relu2_1,relu3_1,和relu4_1分别作为输入。使用16,8和4三种块大小,所以它们相同的32像素大小的感受域。前三个结果示于图8显示:
较低的层(relu2_1)产生更清晰的外观,但在损失了一定结构;
高层(relu4_1)保留粗结构较好,但在用于引导场景有僵化的风险;
relu3_1提供质量和灵活性之间的良好平衡。
然后,像素块尺寸的影响如下:将输入层 D D D 固定为relu3_1,比较4、16、8三个块尺寸的结果。最后结果在图8显示。这样的像素块大小改变也影响模型的刚性:较小的块增加了灵活性;更大的块有利于维护结构。

图9 不同深度的判别神经网络。输入纹理是来自“ropenet”的‘常春藤’[14,23 ],和毕加索的‘自画像1907’。
复杂性: 现在研究(1)在网络中的层的数量和(2)在每个层中的信道数的影响。
作者首先通过去除卷积层改变 D D D 。这样做可以降低网络深度,并且因此降低合成的质量(第一列,图 9)。
将这一卷积层重新加入能够产生更加平滑的合成(第二列,图 9)。
然而,生成质量并不随着卷积层的增加而改善(第三列,图 9)。
测试 D D D ,有4,64,和128个信道的卷积层,作者观察到,降低通道数量通常导致更坏的结果(第四列,图 9),但64个信道和128个信道(第二列VS第五列)之间没有显着性差异。最佳的复杂性还取决于实际的纹理。例如,常春藤纹理是相当简单的,所以4个64个通道之间的差异仅是微不足道的。
接着,作者固定判别网络,改变 G G G 。移除所述第一层的卷积时,或减少所有层的信道数目时有一些质量的损失,但作者注意到随着 G G G 的质量提高,效果的改进非常有限。差别并不十分显著。因为所有这些网络都由同一个判别网络 D D D 驱动。没有进一步改进表明来自解卷积过程的一些非平凡信息无法通过前馈过程恢复。尤其,fractionally strided卷积不能够为最大池化层的非线性行为建模,因此经常产生其他模式。这些在同源、没什么纹理的地区很明显。为了避免这些人工产物,并增强文理的可变性,可以为输入图像选择性增加Perlin噪声[28]。
初始化 通常情况下,网络是随机初始化的。然而,作者发现 D D D 具有一定的推广能力。因此,用MDANs将相同的纹理转移到不同的图像时,一个先前训练的网络可以被用于初始化。图10显示了与初始化预训练的判别网络(已经转移50个的人脸图像)仅50次就产生了好的迭代结果。相比之下,随机初始化甚至不在前500次迭代后产生质量相当的结果。用自动编码器去直接初始化 G G G 是有用的,因为它直接把输入特征解码到了原始输入图像上。这实质上接近于反转 VGG_19 的过程,并让整个对抗网络更加稳定地训练。
VGG的作用: 作者也验证了预先训练VGG_19网络的重要性。如图10最后两个画面所示,从粗略的图像训练神经网络得到显著更坏的结果(从像素到类标签[ 29 ])。这也已经由Ulyanov等人观察到[ 32 ]。作者的解释是,很多VGG_19的统计能力从构建开始,就共享特征级联的一组不同的图像,从而比用有限的样本集训练的网络更接近人类视觉感知。

图10 不同的初始化的判别网络。参考纹理是毕加索的“自画像1907”。
5、结果
作者用100个随机选择的ImageNet图像和单个示例纹理训练每个模型。首先使用MDANs产生100张变换后的图像,然后用固定128-128的窗采样截取图像作为MGANs训练数据。共有大约16K的样品。每个训练周期划分大概十二分钟。作者用五个周期训练每个纹理。
图11将本文的结果与其他方法进行比较。本文的方法与基于全局统计的方法[ 8,32 ]有一个非常不同的特性:它更连贯地传递质感,如头发和莉娜的眼睛始终被映射到暗纹理。与此相反,高斯模型[ 8,32 ]留不住这样的一致性,特别是在眼睛[32 ]的结果,并且在整个面部[8 ]的结果没有纹理化。由于使用非参数采样,其他以局部块为基础的方法[15]产生最相干的合成。然而,他们的方法需要像素块匹配,所以显著较慢(这在110秒里产生384-384图像)。本文的方法和Ulyanov等人的方法[ 22 ]在同一级别速度的上运行;两个方法在速度上都显著超过Gatys等的方法[ 7 ](500倍)和Li等的方法[ 15](快5000倍)。
图12进一步讨论基于高斯方法和本文的方法之间的差异[22]。一般来说[ 22 ]中对于样式图像产生更忠实的色彩分布。它还纹理背景更好(以星夜为例),由于能从高斯分布中学到好的特征映射。在另一方面,本文的方法产生更相干的纹理传递函数,并且在复杂条件下比高斯模型更稳定,例如每一个样本中的正面。相比起来[ 32 ]在这样复杂的区域产生太多或太少的纹理。
MGANs可以噪声输入解码成纹理(图13):Perlin噪声图像[图4]通过前向传播到VGG_19以产生用于解码器的特征图。令人吃惊的是,与ImageNet图像训练模型能够解码特征映射到合理的纹理。这表明模型的泛化能力。图13显示了本文的视频解码结果。作为一个前馈过程,本文的方法不仅更快,但也相对较多时间相干性(图14)。
最后但并非最不重要的,作者提供了他们的方法的时间/内存的使用细节。时间测量是基于一个标准的基准框架[ 2 ]:本文的速度与Ulyanov等工作[ 32 ]处于同一水平,他们也使用了前馈方法,执行比以前的解卷积为基础的方法[8,21 ]显著更快。更确切地说,本文两个方法和Ulyanov等人的工作[ 32 ]都能够将512-512的图像以25Hz的频率进行解码,而[ 32]由一个非常小的差距获胜。两种方法的时间成本与图像中的像素的数量成线性比例。例如,本文的方法在256 * 256的图像花费10毫秒,对于512通过-512图像花费40毫秒,1024-1024的图像允许160毫秒。这两种方法都显示比以前的解卷积方法更快的速度,如Gatys等[ 7 ]和Li等[ 15 ]的工作:比Gatys等人快约500倍[ 7 ],比李快5000倍[15 ]。在此期间作者的方法也比大多数传统的基于像素的纹理合成(这依赖于昂贵的近邻搜索)更快。一个可能的例外是一个GPU实现“块匹配” [1],这可能在相当值得比较的速度运行。但它提供了一个神经网络的质量增强(更好的混合,不变性)(比如工作[ 8,21 ])。
内存的角度来看,作者的生成模型采用70MB的内存(包括VGG网络,到Relu4_1层)。在运行时,解码图像所需的存储线性依赖于图像的尺寸:对于256-256图像需要花费大约600 MB内存,和对于512-512图象它需要约2.5Gb内存。可通过细分输入相片成块被减小内存使用,并使用扫描线的方式进行解码。但是,作者没有进一步探讨内存使用的优化。
6、限制
目前的方法在非纹理数据上效果欠佳。例如,它未能在两个人脸照片之间传输面部特征。这是因为面部特征不能被视为纹理,或者需要的语义来理解(例如表达,姿势,性别等)。一个可能的解决方案是将模型对象类[29]的学习模式的局部统计数据更好的结合,作为一种条件。为了合成照片般逼真纹理,Li[ 21 ]的方法通常会产生更好的结果,由于它禁止数据失真非参数采样。然而,他们的模型的刚性限制了其应用领域。作者方法在变形的纹理效果更好,而且运行显著较快。
与基于高斯的模型[7,22 ]不同,本文的模型有一个非常不同的特征。通过捕获一个全球性的特征分布,这些方法都能够更好地保护全球的“外观和感觉”的例子质感。相比之下,本文的模型会从全局颜色分布偏离。
由于本文的模型学习同一内容的不同描绘之间的映射,它需要的特征具有不变性。为此,作者预先训练VGG_19网络,使得在处理固定背景(天空,失焦区域等)的能力较弱,由于VGG_19是弱激活的。在一般统计数据为基础的方法[ 8,32 ]为具有弱内容的区域生成更好的质感,而且本文的方法对于可识别的区域效果更好。将这两种方法的优势结合是以后的有价值的工作。
最后,作者讨论MDANs和MGANs的结果之间的显著差异。MGANs的输出往往是与样例质地较为一致,这说明MGANs’从大数据中学习的优势。MGANs在平坦的区域弱点由于缺乏迭代优化的、更复杂的结构,如循环性神经网络可以提供状态信息来改善结果。
7、结论
本文的关键结论是对抗性生成网络可在一个马尔可夫设置下被应用到学习相同内容的不同风格描绘之间的映射。作者开发了从单一纹理的样本培训,并从ImageNet随机选择图像完全生成模型。经过培训后,模型可以从棕色噪声解码逼真的纹理或照片变成艺术品。本文的模型在保持一致的纹理复杂的图像内容方面相比起基于统计方法一定的优势[8,32 ]。
本文的方法是在学习的生成模型图像的方向只差一步。对于今后的工作可以研究在大数据方案下更广泛的框架,不仅学会马尔可夫模型,但还包括粗尺度结构模型。这种额外的不变性图像布局可以打开的方式也可以使用更多的训练数据的马尔可夫模型,从而在更大的类具有较强的推广能力允许更多复杂的解码器。
致谢
这项工作由英特尔视觉计算研究所和美因茨计算科学中心部分支持。感谢Bertil Schmidt和Christian Hundt提供额外的计算资源。
参考文献
- Barnes, C., Shechtman, E., Finkelstein, A., Goldman, D.B.: Patch match: A randomized correspondence algorithm for structural image editing. Siggrah pp. 24:1{ 24:11 (2009) 2, 14
- Chintala, S.: Easy benchmarking of all publicly accessible implementations of convnets. https://github.com/soumith/convnet-benchmarks (2015) 13
- Denton, E.L., Fergus, R., Szlam, A., Chintala, S.: Deep generative image models using a laplacian pyramid of adversarial networks. In: NIPS (2015) 1, 3
- Dosovitskiy, A., Brox, T.: Generating images with perceptual similarity metrics based on deep networks. CoRR abs/1602.02644 (2016), http://arxiv.org/abs/1602. 02644 3, 6
- Dosovitskiy, A., Springenberg, J.T., Brox, T.: Learning to generate chairs with convolutional neural networks. CoRR abs/1411.5928 (2014), http://arxiv.org/abs/1411.5928 3
- Efros, A.A., Freeman, W.T.: Image quilting for texture synthesis and transfer. In: Siggraph. pp. 341{346 (2001) 1, 2
- Gatys, L.A., Ecker, A.S., Bethge, M.: Texture synthesis and the controlled generation of natural stimuli using convolutional neural networks. In: NIPS (May 2015), http://arxiv.org/abs/1505.07376 3
- Gatys, L.A., Ecker, A.S., Bethge, M.: A neural algorithm of artistic style (2015), arXiv preprint; http://arxiv.org/abs/1508.06576 1, 2, 3, 4, 11, 12, 13, 14, 15
- Gauthier, J.: Conditional generative adversarial nets for convolutional face generation. http://www.foldl.me/2015/conditional-gans-face-generation/ (2015) 3
- Goodfellow, I., Pouget-Abadie, J., Mirza, M., Xu, B., Warde-Farley, D., Ozair, S., Courville, A., Bengio, Y.: Generative adversarial nets. In: NIPS. pp. 2672{2680 (2014) 1, 3, 4, 6, 7
- Gregor, K., Danihelka, I., Graves, A., Wierstra, D.: DRAW: A recurrent neural network for image generation. CoRR abs/1502.04623 (2015), http://arxiv.org/abs/1502.04623 1, 3
- Hertzmann, A., Jacobs, C.E., Oliver, N., Curless, B., Salesin, D.H.: Image analogies. In: Siggraph. pp. 327{340 (2001) 2
- Im, D.J., Kim, C.D., Jiang, H., Memisevic, R.: Generating images with recurrent adversarial networks. CoRR abs/1602.05110 (2016), http://arxiv.org/abs/1602.05110 3
- Johnson, J., Alahi, A., Li, F.F.: Perceptual losses for real-time style transfer and super-resolution. CoRR abs/1603.08155 (March, 2016), http://arxiv.org/abs/1603.08155v1 3, 12
- Kingma, D.P., Ba, J.: Adam: A method for stochastic optimization. CoRR abs/1412.6980 (2014), http://arxiv.org/abs/1412.6980 6
- Kingma, D.P., Welling, M.: Auto-encoding variational bayes. CoRR abs/1312.6114 (2013), http://arxiv.org/abs/1312.6114 1, 3
- Kulkarni, T.D., Whitney, W., Kohli, P., Tenenbaum, J.B.: Deep convolutional inverse graphics network. CoRR abs/1503.03167 (2015), http://arxiv.org/abs/1503.03167 3
- Kwatra, V., Essa, I., Bobick, A., Kwatra, N.: Texture optimization for example based synthesis. Siggraph 24(3), 795{802 (2005) 6
- Kwatra, V., Schodl, A., Essa, I., Turk, G., Bobick, A.: Graphcut textures: Image and video synthesis using graph cuts. ACM Trans. Graph. 22(3), 277{286 (Jul 2003) 9, 10
- Larsen, A.B.L., S nderby, S.K., Winther, O.: Autoencoding beyond pixels using a learned similarity metric. CoRR abs/1512.09300 (2015), http://arxiv.org/abs/1512.09300 3
- Li, C., Wand, M.: Combining markov random elds and convolutional neural networks for image synthesis. CoRR abs/1601.04589 (2016), http://arxiv.org/abs/1601.04589 1, 2, 3, 4, 11, 13, 14
- Liu, Z., Luo, P., Wang, X., Tang, X.: Deep learning face attributes in the wild. In: ICCV (2015) 7
- Mahendran, A., Vedaldi, A.: Understanding deep image representations by inverting them. In: CVPR (2015) 3, 5
- Mansimov, E., Parisotto, E., Ba, L.J., Salakhutdinov, R.: Generating images from captions with attention. CoRR abs/1511.02793 (2015), http://arxiv.org/abs/1511.02793 3
- Mordvintsev, A., Olah, C., Tyka, M.: Inceptionism: Going deeper into neural networks. http://googleresearch.blogspot.com/2015/06/inceptionism-going-deeper-into-neural.html (2015) 2, 3
- Nguyen, A.M., Yosinski, J., Clune, J.: Multifaceted feature visualization: Uncovering the di erent types of features learned by each neuron in deep neural networks. CoRR abs/1602.03616 (2016), http://arxiv.org/abs/1602.03616 3
- Oord, A.V.D., Kalchbrenner, N., Kavukcuoglu, K.: Pixel recurrent neural networks. CoRR abs/1601.06759 (2016), http://arxiv.org/abs/1601.06759 3
- Perlin, K.: An image synthesizer. SIGGRAPH 19(3), 287{296 (1985) 10 Radford, A., Metz, L., Chintala, S.: Unsupervised representation learning with deep convolutional generative adversarial networks. CoRR abs/1511.06434 (2015), http://arxiv.org/abs/1511.06434 2, 3, 5, 7, 11, 14
- Simonyan, K., Zisserman, A.: Very deep convolutional networks for large-scale image recognition. CoRR (2014), http://arxiv.org/abs/1409.1556 2
- Springenberg, J., Dosovitskiy, A., Brox, T., Riedmiller, M.: Striving for simplicity: The all convolutional net (2015), http://lmb.informatik.uni-freiburg.de/Publications/2015/DB15a 2
- Ulyanov, D., Lebedev, V., Vedaldi, A., Lempitsky, V.: Texture networks: Feed forward synthesis of textures and stylized images. CoRR abs/1603.03417 (March, 2016), http://arxiv.org/abs/1603.03417v1 3, 4, 7, 11, 12, 13, 14, 15
- Wei, L.Y., Levoy, M.: Fast texture synthesis using tree-structured vector quantization. In: Siggraph. pp. 479{488 (2000) 1
- Xie, J., Lu, Y., Zhu, S.C., Wu, Y.N.: A theory of generative convnet. CoRR arXiv:1602.03264 (2016), http://arxiv.org/abs/1602.03264 3, 6, 8, 10
- Yan, X., Yang, J., Sohn, K., Lee, H.: Attribute2image: Conditional image generation from visual attributes. CoRR abs/1512.00570 (2015), http://arxiv.org/abs/1512.00570 3
- Yosinski, J., Clune, J., Nguyen, A.M., Fuchs, T., Lipson, H.: Understanding neural networks through deep visualization. CoRR abs/1506.06579 (2015), http://arxiv.org/abs/1506.06579 3
- Zeiler, M.D., Fergus, R.: Visualizing and understanding convolutional networks. In: ECCV. pp. 818{833 (2014) 2, 3

