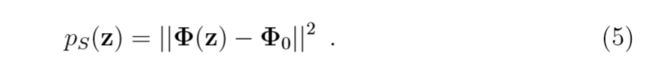Kernel PCA for Novelty Detection

Hoffmann H. Kernel PCA for novelty detection[J]. Pattern Recognition, 2007, 40(3): 863-874.

引

Novelty Detection: 给我的感觉有点像是奇异值检测，但是又不对，训练样本应该默认是好的样本。这个检测应该就是圈个范围，告诉我们在这个范围里的数据是这个类的，外面的不是这个类的，所以论文里也称之为：one-class classification

论文就是利用kernel PCA来寻找这么一个边界（虽然我不知道这个边界是怎么获得的），并讨论了kernel的参数以及载荷向量个数q的选取。

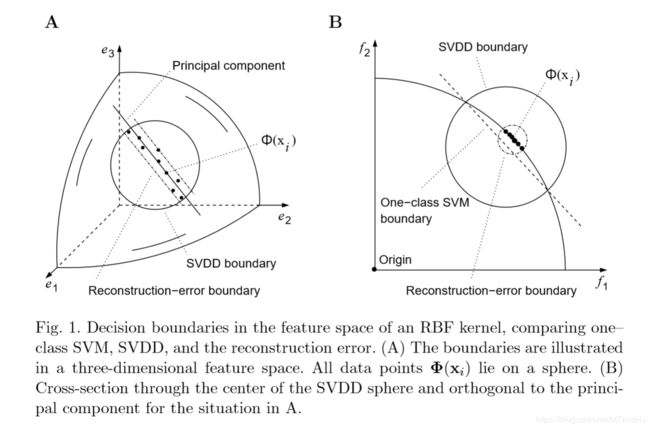
作者给出了几种方法的比较（SVM及其变种），说明了利用reconstruction error设定边界的优势。

主要内容

大部分符合和kernel PCA的符号是一致的，这里就不多赘述了，先给出reconstruction error的定义：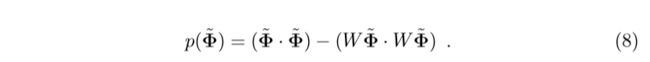

其中\(W\)的行向量是特征向量（高维空间中的，这里只是如此表示，就像kernel PCA精髓，不必显示地表示出），\(\tilde{\Phi}\)是中心化后的\(\Phi\)。
很显然，上面的式子的第二项实际上就是\(\tilde{\Phi}\)在子空间中投影的部分的内积，所以\(p(\tilde{\Phi})\)就是重构的被舍弃的误差。很自然，同一类数据\(p(\tilde{\Phi})\)的值应该相对比较大。所以\(W\)选择的特征向量是主特征向量（对应的特征值比较大）。

注：可以发现\(p(\cdot) \ge 0\)

这个式子如何计算呢？

其中\(\Phi_0 = 1/n \sum \limits_{i=1}^n \Phi(x_i)\)，于是，\((\tilde{\Phi}(z), \tilde{\Phi}(z))=p_S(z)\)可以用下式来计算:

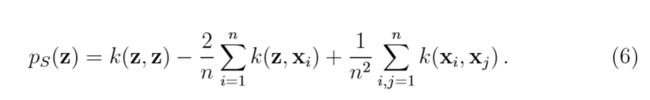
注： 第二项与Parzen Windows有很大关联
令：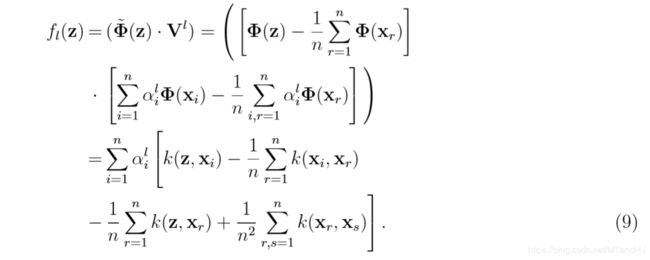

其中\(V^l = \sum \limits_{i=1}^n \alpha_i^l \tilde{\Phi}(x_i)\)为第\(l\)个特征向量。
易得：
\[ (W\tilde{\Phi}(z), W\tilde{\Phi}(z)) = \sum \limits_{i=1}^q f_l(z)^2 \]
所以：

需要注意的是(6)和(9)中有许多重复计算的地方，可以先计算这些部分再进行整理会简单很多。

注：kernel为高斯核的时候，\(k(x, x)\)的值是固定，可以理解为高维空间中向量的模大小一致，个人认为这是非常好的一个性质，这也是在数值实验中，高斯核的性能远远超出多项式核的原因（至少在这个方面是如此的）。

\(\sigma^2\)的选择

高斯核的形态为：
\[ k(x,y) = \exp \{-\frac{\|x-y\|^2}{2\sigma^2}\} \]
当\(\sigma \rightarrow0\)的时候，\(k(x,y) \rightarrow0\)，这时\(\Phi(x), \Phi(y)\)彼此正交，所以\(\sigma\)不应当太小。

当\(\sigma \gg \max \|x_i -x_j\|\)的时候：
\[ k(x,y) \approx 1 - \|x-y\|^2/(2\sigma^2) \]
可以证明，此时的reconstruction error的效用采用\(k(x,y)\)和采用\((x\cdot y)\)的类似的。
首先：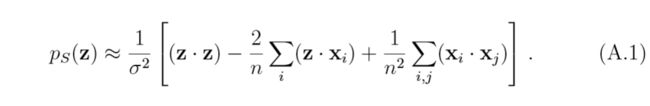


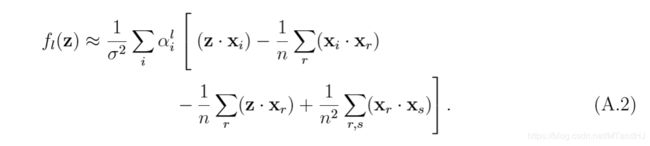
均只差一个比例常数\(\frac{1}{\sigma^2}\)，又：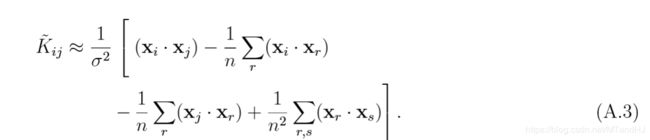

也差一个比例常数\(\frac{1}{\sigma^2}\)，所以此时采用\(k(x,y)\)和\((x\cdot y)\)并没有太大的差别。这意味着，\(\sigma^2\)不能太大。

最后再提一下\(q\)的选择，显然\(q\)应当足够大，这个参数可以通过特征值来选择。

数值实验

数值实验采用的kernel均为高斯核，多项式核效果核论文中的差别有点大就不提了。

矩形框

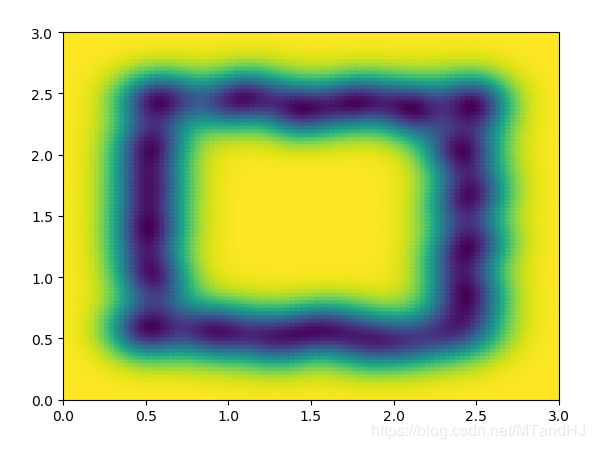
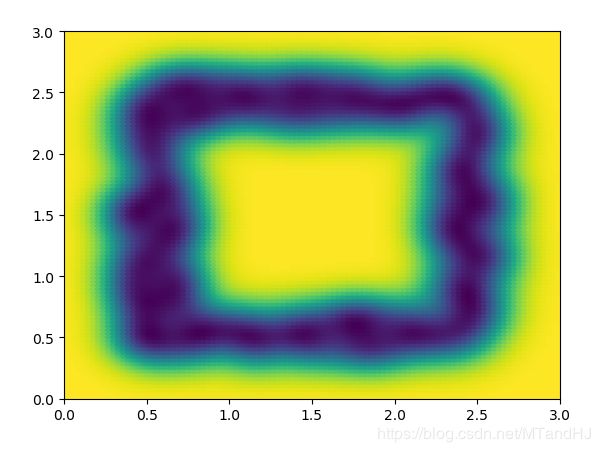
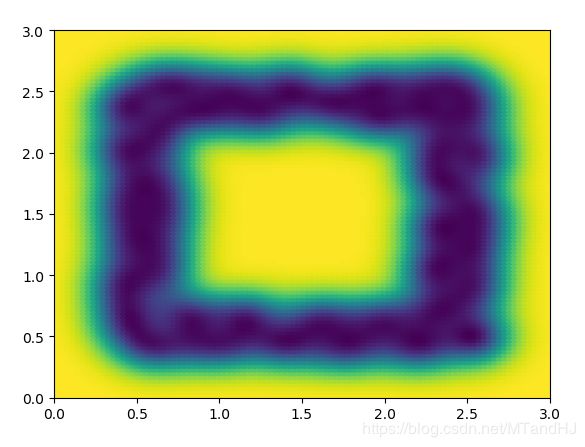
数据是如此分布的(只是框定了范围，里面的数据点是从均匀分布中选取的)：0.4 ~ 0.6， 2.3 ~ 2.6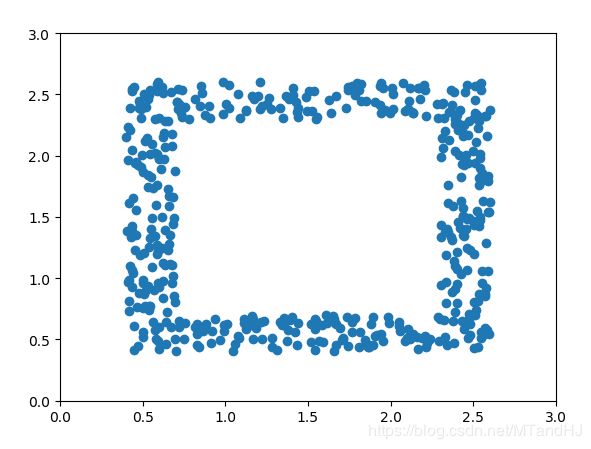

q = 20, \(\sigma^2=0.2\)

q = 20, \(\sigma^2 = 0.4\)

q = 30 \(\sigma^2= 0.2\)

q = 30 \(\sigma^2=0.4\)

q = 40 \(\sigma^2=0.2\)

q = 40 \(\sigma^2=0.4\)

q = 80 \(\sigma^2=0.1\)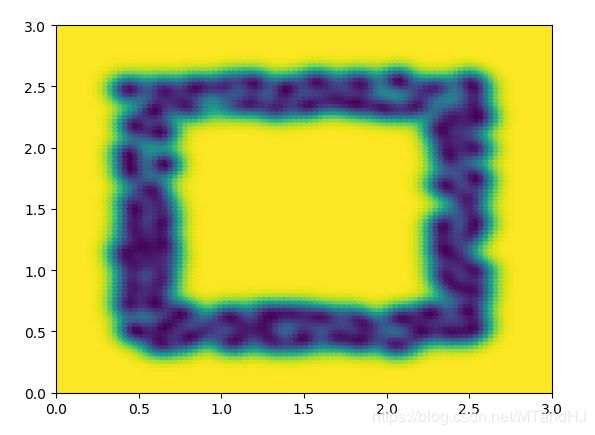

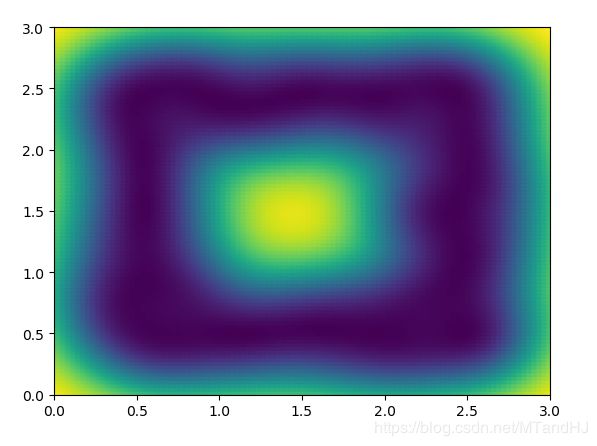
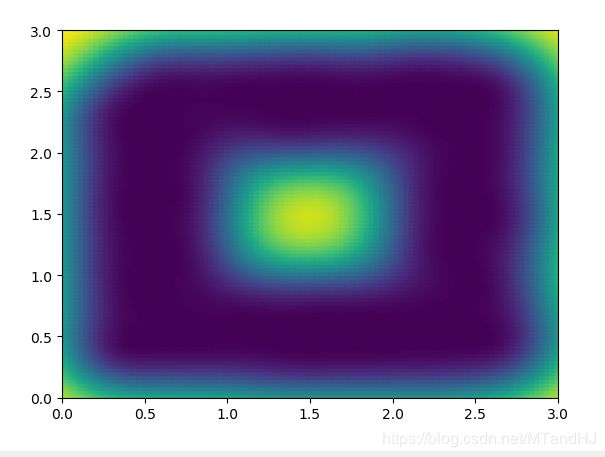
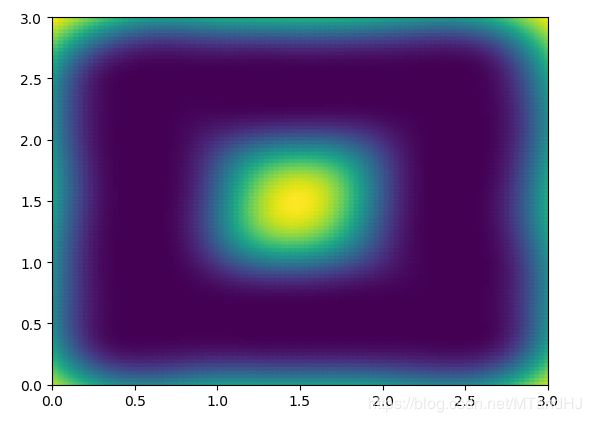
q=80 \(\sigma^2=0.2\)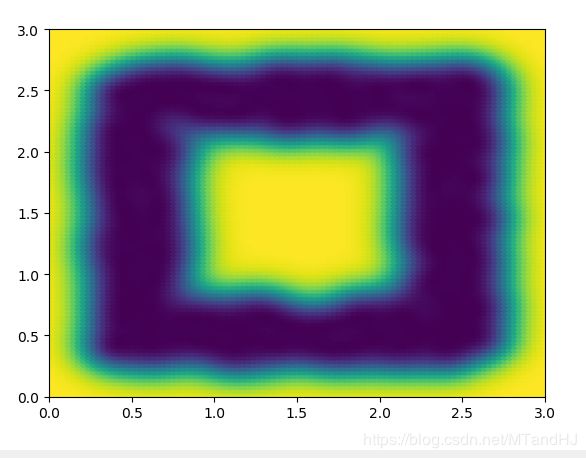

下面是q=50.\(\sigma^2=50\)的error在y=1.5处左右的值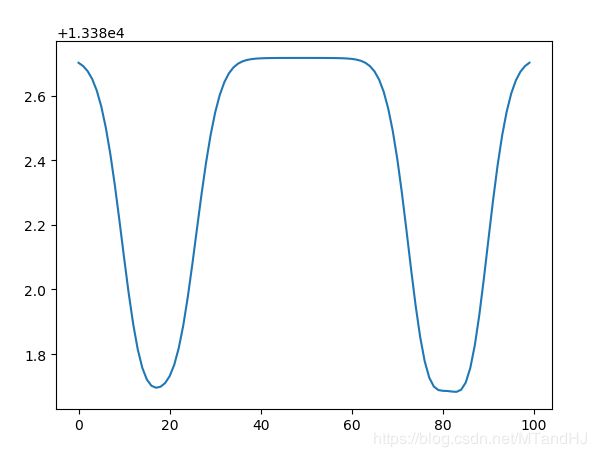

spiral

原始数据如下(只是这个形状的)：
\[ x = (0.07t + a)cos(t) + 1.5 \\ y = (0.07t + a)sin(t) + 1.5 \\ a \in [0,0.1] \]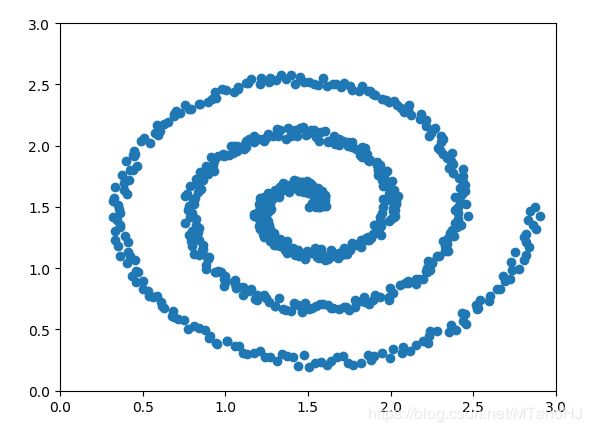

q = 40 \(\sigma^2 = 0.15\)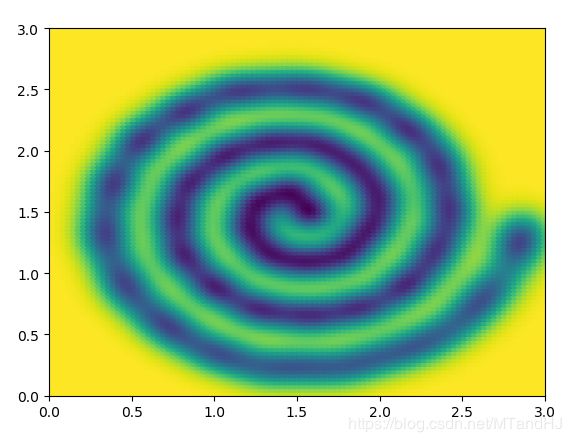

q = 40 \(\sigma^2=0.2\)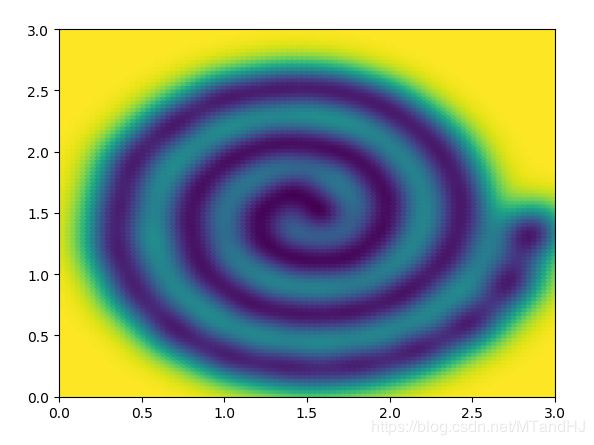

下面是q=40,\(\sigma^2=0.15\)的\(y=1.5\)左右处的error值：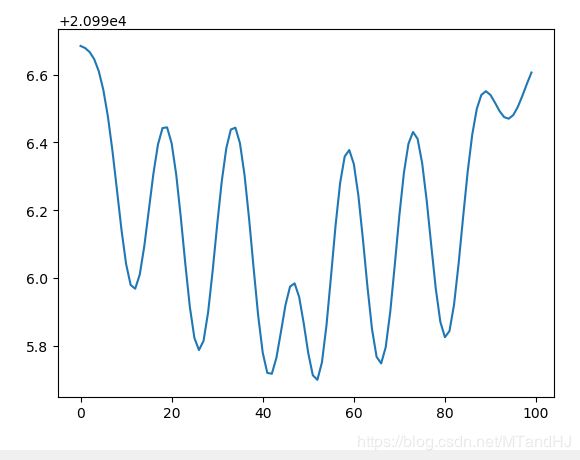

代码

import numpy as np



class KernelPCA:

    def __init__(self, data, kernel=2, pra=0.4):
        self.__n, self.__d = data.shape
        self.__data = np.array(data, dtype=float)
        self.kernel = self.kernels(kernel, pra)
        self.__K = self.center()

    @property
    def shape(self):
        return self.__n, self.__d

    @property
    def data(self):
        return self.data

    @property
    def K(self):
        return self.__K

    @property
    def alpha(self):
        return self.__alpha

    @property
    def eigenvalue(self):
        return self.__value

    def kernels(self, label, pra):
        """
        数据是一维的时候可能有Bug
        :param label: 1:多项式;2:exp
        :param pra:1: d; 2: sigma
        :return: 函数 或报错
        """
        if label is 1:
            return lambda x, y: (x @ y) ** pra
        elif label is 2:
            return lambda x, y: \
                np.exp(-(x-y) @ (x-y) / (2 * pra ** 2))
        else:
            raise TypeError("No such kernel...")

    def center(self):
        """中心化"""
        oldK = np.zeros((self.__n, self.__n), dtype=float)
        one_n = np.ones((self.__n, self.__n), dtype=float)
        for i in range(self.__n):
            for j in range(i, self.__n):
                x = self.__data[i]
                y = self.__data[j]
                oldK[i, j] = oldK[j, i] = self.kernel(x, y)
        return oldK - 2 * one_n @ oldK + one_n @ oldK @ one_n

    def ordereig(self, A):
        """晕了，没想到linalg.eig出来的特征值不一定是按序的"""
        value, vector = np.linalg.eig(A)
        order = np.argsort(value)[::-1]
        value = value[order]
        vector = vector.T[order].T
        return value, vector

    def processing(self):
        """实际上就是K的特征分解,再对alpha的大小进行一下调整"""
        value, alpha = self.ordereig(self.__K)
        index = value > 0
        value = value[index]
        alpha = alpha[:, index] * (1 / np.sqrt(value))
        self.__alpha = alpha
        self.__value = value / self.__n

    def score(self, x):
        """来了一个新的样本，我们进行得分"""
        k = np.zeros(self.__n)
        for i in range(self.__n):
            y = self.__data[i]
            k[i] = self.kernel(x, y)
        return k @ self.__alpha


class NoveltyDetection:

    def __init__(self, data, q, kernel=2, pra=0.4):
        self.kernel = self.kernels(kernel, pra) #选择kernel
        kernelPCA = KernelPCA(data, kernel, pra) #进行kernel PCA
        kernelPCA.processing() #进行kernel PCA
        self.__alpha = kernelPCA.alpha[:, :q] #获取相应的alpha
        self.__K = kernelPCA.K #获取K
        self.basedata() #用于计算reconstruction error
        self.__data = np.array(data, dtype=float)
        self.__shape = kernelPCA.shape
        del kernelPCA #我不知道这么做是否有意义

    @property
    def alpha(self):
        return self.__alpha

    @property
    def K(self):
        return self.__K

    @property
    def data(self):
        return self.__data

    @property
    def shape(self):
        return self.__shape

    def kernels(self, label, pra):
        """
        数据是一维的时候可能有Bug
        :param label: 1:多项式;2:exp
        :param pra:1: d; 2: sigma
        :return: 函数 或报错
        """
        if label is 1:
            return lambda x, y: (x @ y) ** pra
        elif label is 2:
            return lambda x, y: \
                np.exp(-(x-y) @ (x-y) / (2 * pra ** 2))
        else:
            raise TypeError("No such kernel...")

    def basedata(self):
        self.unitmean = np.mean(self.K, 1)
        self.allmean = np.mean(self.K)

    def detection(self, z):
        n = self.shape[0]
        phiz = np.zeros(n)
        for i in range(n):
            phiz[i] = self.kernel(z, self.data[i])
        psz = self.kernel(z, z) - np.mean(phiz) * 2 + \
            self.allmean
        temp1 = -np.mean(phiz) + self.allmean
        temp2 = np.array([
            phiz[i] - self.unitmean[i] + temp1
            for i in range(n)
        ], dtype=float)
        pz = psz - np.sum((self.alpha.T @ temp2) ** 2)

        return pz
"""
import matplotlib.pyplot as plt

x = (np.random.rand(1000) + 0.4 / 2.2) * 2.2
y = (np.random.rand(1000) + 0.4 / 2.2) * 2.2

func_and = lambda x: x[0] and x[1]
func_or = lambda x: x[0] or x[1]
def findindex(x, x1, x2, x3, x4):
    index1 = zip(x > x1, x < x2)
    index2 = zip(x > x3, x < x4)
    index3 = list(map(func_and, index1))
    index4 = list(map(func_and, index2))
    index = list(map(func_or, zip(index3, index4)))
    return index

xindex = findindex(x, 0.4, 0.7, 2.3, 2.6)
yindex = findindex(y, 0.4, 0.7, 2.3, 2.6)
index = list(map(func_or, zip(xindex, yindex)))
x = x[index]
y = y[index]
data = np.column_stack((x, y))

test = NoveltyDetection(data, 40, kernel=2, pra=0.2)
Y, X = np.mgrid[0:3:100j, 0:3:100j]
newdata = np.zeros(X.shape)
for i in range(X.shape[0]):
    for j in range(X.shape[1]):
        z = np.array([X[i, j], Y[i, j]])
        newdata[i, j] = test.detection(z)

plt.scatter(X, Y, c=newdata)
plt.xlim(0, 3)
plt.ylim(0, 3)
plt.show()
"""

转载于:https://www.cnblogs.com/MTandHJ/p/10805921.html