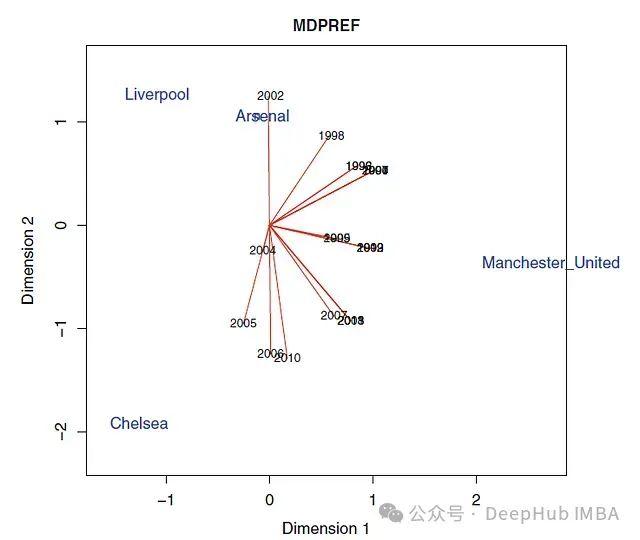
多维偏好分析(Multidimensional Preference Analysis, MPA)是一种在市场营销、心理学和公共政策等领域广泛应用的分析工具,用于研究多维度下的复杂偏好决策过程。在高维数据集中,当属性与偏好之间存在非线性关系或维度重叠时,偏好的理解和可视化呈现出显著的技术挑战。
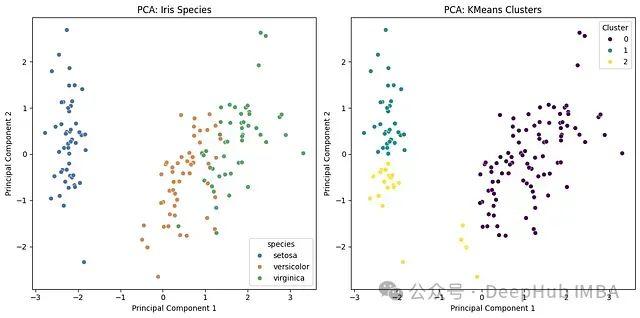
本文本将研究采用主成分分析(Principal Component Analysis, PCA)和K均值聚类算法对鸢尾花数据集进行降维分析和模式识别。PCA用于数据降维的同时保持关键方差信息,聚类算法则用于探索数据的内在分组特征。分析表明PCA能够有效实现物种分类,在二维空间中保留95.8%的数据方差。K均值聚类识别出的模式与实际物种分类具有高度一致性,同时也反映出相近类别(如变色鸢尾和弗吉尼亚鸢尾)之间的重叠特征。
基于PCA和聚类分析的多维偏好分析方法为高维偏好数据的简化和理解提供了可靠的分析框架。该方法能够有效揭示数据中的隐含模式,对各领域的实际决策具有重要的应用价值。
引言
消费者行为研究中的一个核心问题是理解不同消费群体的品牌偏好差异。例如某些消费者偏好奢侈品牌,而另一些则更注重实用性;某款智能手机能获得广泛认可,而具有相似技术参数的另一款却未能引起市场共鸣。这种复杂的选择行为很少由单一因素决定,而是多种因素共同作用的结果。多维偏好分析(MPA)[1-5]正是为解决这类复杂决策问题而开发的分析工具。
通过维度分析,我们可以将看似混沌的选择行为转化为可理解的模式。
偏好的多维特性分析
偏好决策很少呈现线性或单维特征。在实际情况中,个体和群体往往基于多个评价维度进行选择。以旅游目的地选择为例,消费者的决策过程涉及费用、距离、气候条件和活动选项等多个维度的综合权衡。多维偏好分析为研究者提供了一种系统方法,用于解析这些复杂的决策过程,深入理解不同属性对决策的影响机制。
多维偏好分析主要探讨两个核心问题:
- 识别决策过程中的关键影响因素
- 分析这些因素之间的交互作用及其对偏好形成的影响机制
多维偏好分析通过主成分分析、多维尺度分析或联合分析等统计方法,将抽象的偏好数据转化为可量化的分析结果。这种方法不仅具有学术价值,还为市场营销人员、政策制定者、产品设计师和人力资源管理者提供了实践指导。
多维偏好分析的技术框架
多维偏好分析通常包含以下四个关键步骤:
数据采集:通过问卷调查、选择实验或行为观察收集偏好数据。例如,汽车制造商可能会要求消费者对燃油效率、价格和外观设计等因素进行重要性评分。
维度降低:运用统计模型将复杂的多属性数据降维至可视化空间,以便发现数据中的潜在模式,如具有相似偏好特征的消费者群体。
偏好映射:构建感知图谱,直观展示产品属性、消费者偏好等要素之间的关系,为目标市场定位提供依据。
分析应用:基于多维偏好分析的结果指导决策,如产品改进、营销策略优化或服务体系完善。
多维偏好分析的应用领域
多维偏好分析在多个领域具有重要的应用价值:
市场营销与消费者研究:通过分析客户忠诚度和购买决策的影响因素,帮助企业优化营销策略。例如,零售商可以利用多维偏好分析在价格敏感性和品牌价值之间寻找平衡点。
公共政策制定:帮助政府部门评估社区需求优先级,实现资源的优化配置。
医疗卫生服务:在以患者为中心的医疗实践中,协助医疗人员综合评估治疗效果、经济成本和患者体验等多个维度。
人力资源管理:用于员工满意度测评和福利体系设计,确保人力资源政策能够满足员工的多维需求。# 案例分析:智能手机市场的多维偏好研究
在一项针对智能手机市场的消费者偏好研究中,研究者收集了消费者对电池续航能力、摄像系统性能、价格水平和品牌价值等属性的评价数据。通过多维偏好分析,研究发现消费者可以划分为两个主要群体:一类消费者更重视产品的技术创新性和品牌影响力,另一类则更关注性价比和基础功能的可靠性。这些发现为制造商的产品线规划和市场细分策略提供了重要参考,有助于提升市场份额和用户满意度。
实验研究
以下代码展示了使用
Iris数据集进行多维偏好分析的具体实现过程,主要运用了主成分分析和聚类分析方法。
importpandasaspd
importnumpyasnp
importseabornassns
importmatplotlib.pyplotasplt
fromsklearn.decompositionimportPCA
fromsklearn.preprocessingimportStandardScaler
fromsklearn.metricsimportexplained_variance_score
fromsklearn.clusterimportKMeans
# 导入Iris数据集
iris=sns.load_dataset('iris')
# 显示数据样本
print("Dataset Sample:")
print(iris.head())
# 特征和目标变量分离
features=iris.drop(columns=['species'])
target=iris['species']
# 特征标准化处理
scaler=StandardScaler()
features_scaled=scaler.fit_transform(features)
# 执行PCA降维,保留两个主成分
pca=PCA(n_components=2)
principal_components=pca.fit_transform(features_scaled)
# 构建包含PCA结果的数据框
pca_df=pd.DataFrame(data=principal_components, columns=['PC1', 'PC2'])
pca_df['species'] =target
# 计算解释方差比
explained_variance=pca.explained_variance_ratio_
print("Explained Variance Ratio:", explained_variance)
# 应用KMeans进行聚类分析
kmeans=KMeans(n_clusters=3, random_state=42)
kmeans_labels=kmeans.fit_predict(principal_components)
pca_df['Cluster'] =kmeans_labels
# 计算解释方差得分
variance_score=explained_variance_score(features_scaled, pca.inverse_transform(principal_components))
print("Explained Variance Score (Reconstruction):", variance_score)
# 绘制PCA结果和聚类结果
plt.figure(figsize=(12, 6))
plt.subplot(1, 2, 1)
sns.scatterplot(x='PC1', y='PC2', hue='species', data=pca_df, palette='deep')
plt.title('PCA: Iris Species')
plt.xlabel('Principal Component 1')
plt.ylabel('Principal Component 2')
plt.subplot(1, 2, 2)
sns.scatterplot(x='PC1', y='PC2', hue='Cluster', data=pca_df, palette='viridis')
plt.title('PCA: KMeans Clusters')
plt.xlabel('Principal Component 1')
plt.ylabel('Principal Component 2')
plt.tight_layout()
plt.show()
# 结果分析
print("\nInterpretation:")
print(f"PCA reduced the dataset from 4 dimensions to 2 while retaining {sum(explained_variance) *100:.2f}% of the variance.")
print("The scatter plot shows that PCA effectively separates the species in the Iris dataset.")
print("KMeans clustering also highlights separability, though some overlap is observed.")实验结果阐明了多维数据分析中的关键技术路径,展示了PCA在数据降维和模式识别中的应用价值。
基于物种的PCA分析结果
物种分类效果:PCA投影显著区分了鸢尾花数据集中的三个物种(
setosa、
versicolor、
virginica)。
山鸢尾特征:在第一主成分方向上,山鸢尾与其他两个物种形成明显分离。
变色鸢尾和弗吉尼亚鸢尾的特征重叠:这两个物种在特征空间中表现出部分重叠,说明它们具有相似的形态特征。
方差解释能力:前两个主成分保留了数据集的主要信息,为进一步分析提供了可靠的简化表示。
基于K均值的聚类分析结果
聚类效果:K均值算法将降维后的数据划分为三个群组。
分类准确性*:聚类结果与物种分类具有较高的一致性,尤其是山鸢尾类别表现出良好的可分性。
边界模糊性:在变色鸢尾和弗吉尼亚鸢尾之间存在一定的分类误差,这反映了它们在特征空间中的自然重叠现象。
无监督学习效果:K均值聚类在没有先验标签信息的情况下,能够较好地识别数据集中的自然分组结构。
主要研究发现
降维效果:PCA算法成功将四维数据降至二维表示,同时保持了数据的主要变异信息,为数据可视化和分析提供了有效途径。
聚类效果:K均值聚类在无监督学习条件下,识别出的模式与实际物种分类高度吻合,验证了该方法在探索性数据分析中的实用价值。
应用价值:本研究采用的分析方法可推广应用于客户偏好分析、数据分类以及多维数据集的结构探索等实际问题。
总结
多维偏好分析为复杂决策问题提供了系统的分析框架,能够将抽象的主观数据转化为可量化的分析结果。无论是在市场营销策略制定、新产品开发还是资源配置决策中,多维偏好分析都能为决策者提供有价值的数据支持。通过这种系统化的分析方法,组织能够更好地理解目标群体的需求特征,从而制定更有针对性的决策方案。
研究表明,复杂决策问题的核心在于理解和把握影响决策的关键维度。这不仅需要收集全面的数据,更需要采用适当的分析方法来揭示数据中的深层模式。
针对多维偏好分析在实际应用中遇到的技术难点,未来研究可以从以下几个方面展开:
- 开发更高效的降维算法
- 提升聚类方法在处理重叠数据时的准确性
- 探索新的可视化方法以更好地展示高维数据的特征
参考
SPO: Multi-Dimensional Preference Sequential Alignment With Implicit Reward Modeling
Learning-Augmented K-Means Clustering Using Dimensional Reduction
Active Preference-based Learning for Multi-dimensional Personalization
Turning Big Data into Tiny Data: Constant-size Coresets for K-Means, PCA, and Projective Clustering
Recognising Multidimensional Euclidean Preferences
https://avoid.overfit.cn/post/0d1f44aea5c947e597dc2dc423004990
作者:Everton Gomede, PhD