通信电子电路实验(三)——高频电容反馈型LC振荡器的设计与仿真
文章目录
- 理论背景
- 参数设计
- 直流工作点分析
- 瞬态分析
- I C Q I_{CQ} ICQ 对起振时间和电压幅度的影响
- 回路电容 C 2 C_2 C2,对起振时间、振荡频率的影响。
- 负载电阻 R L R_L RL 对起振时间,输出电压幅值的影响
理论背景
1.只读模块 (分数占比0%)
【实验目的】
-
掌握应用电路仿真软件Pspice/Multisim等对高频电容反馈型LC振荡器的仿真设计方法。
-
掌握高频电容反馈型LC振荡器的直流工作点、反馈系数和负载等变化时对其主要性能如振荡频率、输出电压幅度和起振时间等的影响。
2.只读模块 (分数占比0%)
【实验原理】
高频LC振荡器广泛应用于通信电子系统、射频测试测量仪器、医疗仪器和物体探测装置中,其本质是将直流供电电源的能量转换为交流输出信号,本身不需要外部激励就能自动地实现能量转换,一般由晶体管、选频回路、反馈电路等组成。选频电路采用LC谐振回路的振荡器称为LC振荡器。在通信系统中,LC振荡器可以产生发射机中的载波,或作为接收机的本地振荡器。常用的LC振荡器有电容反馈型和电感反馈型两种类型,其中,电容反馈型振荡器由于高频波形较好,应用更加广泛。
常见的电容反馈型LC振荡器有共基极和共发射极两种结构。共基极组成的典型电路如图1所示,其中L、C1和C2组成振荡回路,Rb1、Rb2为晶体管的直流偏置电阻,Re为发射极电阻,Cb、Cc分别是基极和集电极耦合电容,取值较大,RL为负载电阻。

该振荡器的振荡频率为
f 0 = 1 2 π L C Σ ≈ 1 2 π L C 1 C 2 C 1 + C 2 f_0 = \frac{1}{2\pi\sqrt{LC_\Sigma}}\approx \frac{1}{2\pi\sqrt{L\frac{C_1C_2}{C_1+C_2}}} f0=2πLCΣ1≈2πLC1+C2C1C21
实际仿真时,由于考虑了晶体管结电容的影响,如集电结电容与C1并联,发射结电容与C2并联,实际电路的电容值要比理论计算值大,故振荡频率会低一些。
该振荡器的反馈系数为
F ≈ C 1 C 1 + C 2 F \approx \frac{C_1}{C_1+C_2} F≈C1+C2C1
可见,若通过改变C1或C2来改变反馈系数F,振荡频率也将随之改变。
高频LC振荡器的设计涉及晶体管的选型、晶体管直流工作点的选择、振荡频率的计算、反馈系数的确定和输出信号幅度的调整等。
高频振荡器在选择晶体管时与高频小信号放大器类似,尽量选择特征频率fT较高(大于5~10倍的振荡频率)、结电容小一些的晶体管,同时要求晶体管的 b 值不能太小,否则不容易起振。
振荡器在起振时,晶体管需工作在放大状态,其发射结要导通。为了确保能够起振,需要有足够大的增益A,以满足AF > 1的振幅起振条件,F为反馈系数。起振后,振幅逐渐增大,达到稳定的平衡状态时,AF = 1。增益A的大小与晶体管的直流工作点和负载都相关,也关系到输出电压的幅值。
3.只读模块 (分数占比0%)
【实验内容】
用电路仿真软件Pspice/Multisim仿真设计一个高频电容反馈型LC振荡器,满足以下要求:
-
晶体管采用共基组态;
-
实现无目测失真的正弦波输出;
-
振荡频率在 15 ~ 20 M H z 15~20MHz 15~20MHz之间;
-
输出电压的幅值不小于2V;
-
晶体管的 I C Q = 2 ~ 4 m A I_{CQ}=2~4mA ICQ=2~4mA;
-
反馈系数 F = 0.2 ~ 0.5 F=0.2~0.5 F=0.2~0.5;
-
电源电压VCC为12V;
-
晶体管推荐采用Q2N2222,其 β = 255.9 β=255.9 β=255.9,特征频率 f T ≈ 398 M H z f_T ≈ 398MHz fT≈398MHz。
参数设计
首先我们控制变量,让 L 1 = 1 μ H L1=1\mu H L1=1μH
之后由: f 0 = 1 2 π L C Σ ≈ 1 2 π L C 1 C 2 C 1 + C 2 f_0 = \frac{1}{2\pi\sqrt{LC_\Sigma}}\approx \frac{1}{2\pi\sqrt{L\frac{C_1C_2}{C_1+C_2}}} f0=2πLCΣ1≈2πLC1+C2C1C21
可以估算出 C Σ C_\Sigma CΣ的数量级大概是 1 0 − 10 F 10^{-10}F 10−10F
之后,由于 F ≈ C 1 C 1 + C 2 F \approx \frac{C_1}{C_1+C_2} F≈C1+C2C1,我们就限定 C 1 : C 2 = 1 : 2 C_1:C_2=1:2 C1:C2=1:2,这样F系数一定能满足要求。
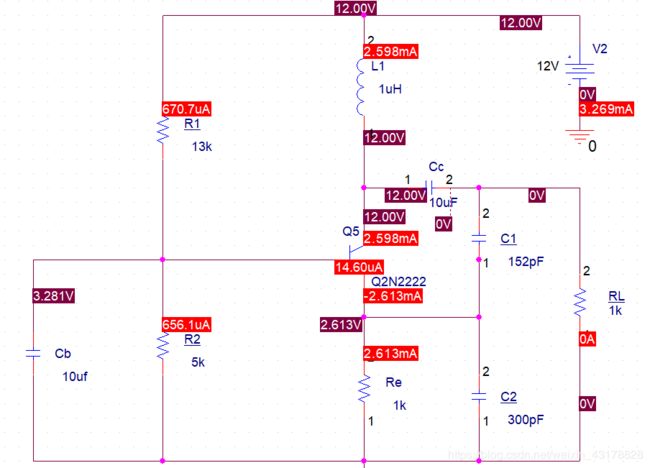
静态工作点方面,我设计成:
| 元器件符号 | 值 |
|---|---|
| R 1 R_1 R1 | 13 K Ω 13K\Omega 13KΩ |
| R 2 R_2 R2 | 5 K Ω 5K\Omega 5KΩ |
| R e R_e Re | 1 K Ω 1K\Omega 1KΩ |
其他元器件主要是经验数据:
| 元器件符号 | 值 |
|---|---|
| C b C_b Cb | 10 μ F 10 \mu F 10μF |
| C c C_c Cc | 10 μ F 10\mu F 10μF |
| R L R_L RL | 1 k Ω 1k\Omega 1kΩ |
直流工作点分析

直流偏置 V B = V C C ⋅ R 2 R 1 + R 2 = 3.3 V V_B=\frac{VCC·R_2}{R_1+R_2}=3.3V VB=R1+R2VCC⋅R2=3.3V
静态工作点
I C Q = 2.598 m A ∈ ( 2 m A , 4 m A ) I_{CQ}=2.598mA\in(2mA, 4mA) ICQ=2.598mA∈(2mA,4mA)
放大倍数
β = I C Q I B Q = 2.598 m A 14.60 μ A = 177.9 \beta= \frac{I_{CQ}}{I_{BQ}}=\frac{2.598mA}{14.60\mu A}=177.9 β=IBQICQ=14.60μA2.598mA=177.9
工作状态
V B E = 3.281 V − 2.613 V = 0.668 V V_{BE}=3.281V-2.613V=0.668V VBE=3.281V−2.613V=0.668V
V C E = V C C − V E = 9.387 V > > V s a t = 0.3 V V_{CE}=VCC-VE=9.387V\gt\gt V_{sat}=0.3V VCE=VCC−VE=9.387V>>Vsat=0.3V
因此可以确定是处于放大区
瞬态分析
| 参数 | 值 | 图片证明 |
|---|---|---|
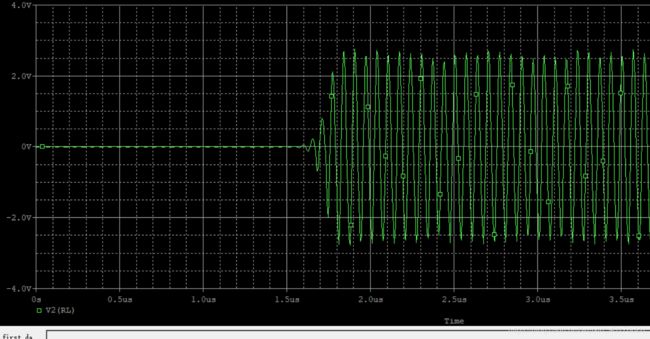
| 幅值 | 4.67V | 图一 |
| 起振时间 | 1.3us | 图一 |
| 频率 | 15MHz | 图二 |
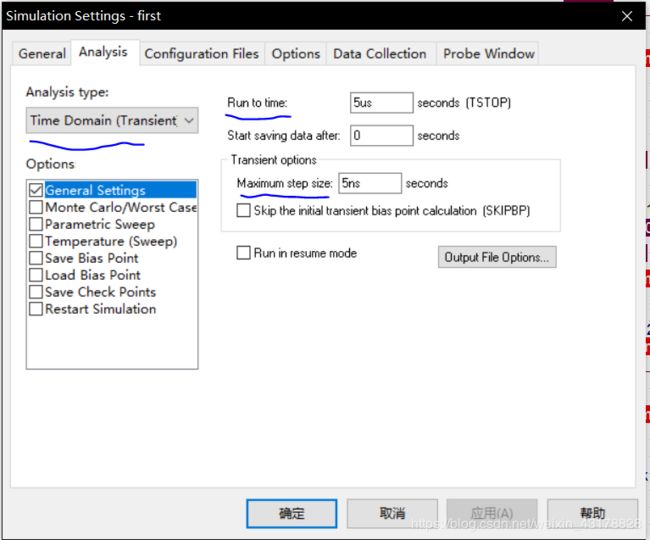
- Analysis type 分析方式 选择时域分析
- Run to time 仿真的总时间 选择大概5~10us左右就好 按自己构图的喜好调节
- Maximum step size 这里一般选择5ns为好
这里如果没有设置,你的波形就会是这个样子:

因此这个设置非常关键!
I C Q I_{CQ} ICQ 对起振时间和电压幅度的影响
- R e = 1.5 k Ω R_e=1.5k\Omega Re=1.5kΩ

I C Q = 1.749 m A I_{CQ}=1.749mA ICQ=1.749mA
V C P P = 2.71 V V_{CPP}=2.71V VCPP=2.71V
t 起 振 时 间 = 1.61 u s t_{起振时间}=1.61us t起振时间=1.61us
- R e = 2 k Ω R_e=2k\Omega Re=2kΩ
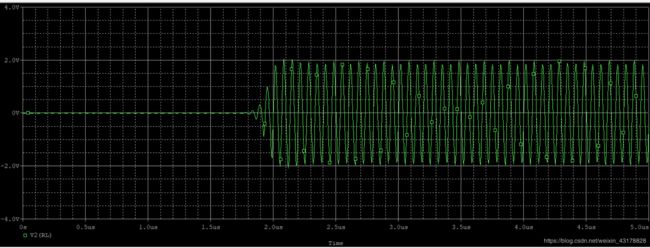

I C Q = 1.320 m A I_{CQ}=1.320mA ICQ=1.320mA
V C P P = 1.93 V V_{CPP}=1.93V VCPP=1.93V
t 起 振 时 间 = 1.83 u s t_{起振时间}=1.83us t起振时间=1.83us
- R e = 2.5 k Ω R_e=2.5k\Omega Re=2.5kΩ
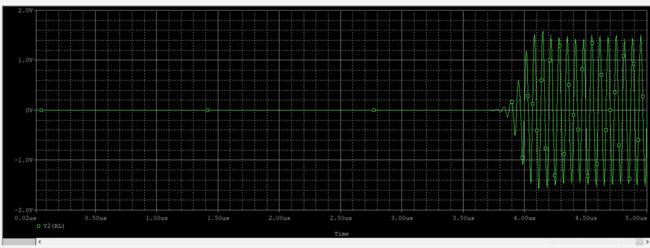
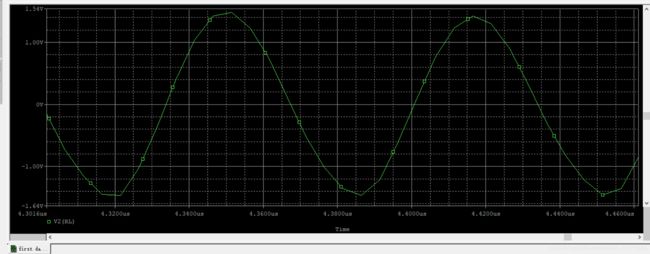
I C Q = 1.060 m A I_{CQ}=1.060mA ICQ=1.060mA
V C P P = 1.49 V V_{CPP}=1.49V VCPP=1.49V
t 起 振 时 间 = 3.77 u s t_{起振时间}=3.77us t起振时间=3.77us
对比以上数据,我们可以得到下表:

因此,在一定范围内, R e R_{e} Re与 V C P P V_{CPP} VCPP和 I C Q I_{CQ} ICQ均呈负相关关系,同时与 t 起 振 时 间 t_{起振时间} t起振时间呈现正相关关系。
回路电容 C 2 C_2 C2,对起振时间、振荡频率的影响。
- 600pF
波形图 t 起 振 时 间 = 1.31 u s t_{起振时间}=1.31us t起振时间=1.31us
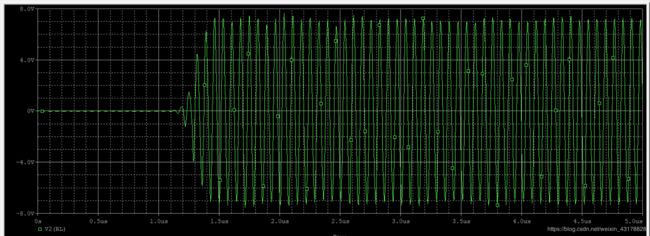
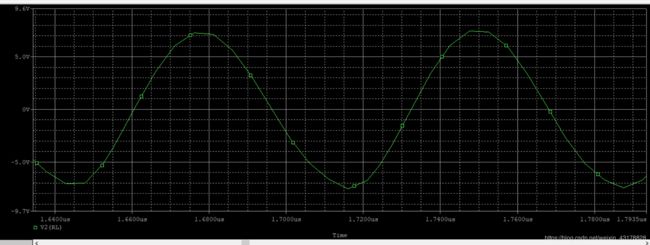
傅里叶分析 频谱图 f 0 = 14.0 M H z f_0=14.0MHz f0=14.0MHz

- 900pF t 起 振 时 间 = 1.57 u s t_{起振时间}=1.57us t起振时间=1.57us


傅里叶分析 频谱图 f 0 = 13.4 M H z f_0=13.4MHz f0=13.4MHz
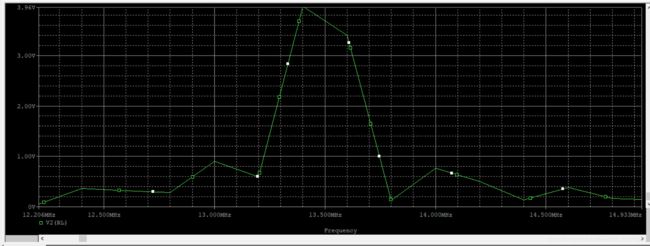
- 1200pF
波形图 t 起 振 时 间 = 1.83 u s t_{起振时间}=1.83us t起振时间=1.83us

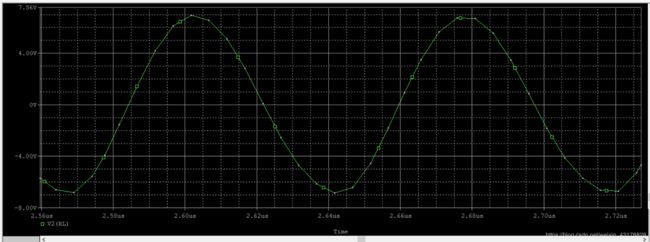
傅里叶分析 频谱图 f 0 = 13.2 M H z f_0=13.2MHz f0=13.2MHz

- 总结


由此可知,在一定范围内,
回路电容 C 2 C_2 C2与起振时间 t 起 振 时 间 t_{起振时间} t起振时间呈现正相关,而与振荡频率呈现负相关
又因为 F = C 1 C 1 + C 2 F = \frac{C_1}{C_1+C_2} F=C1+C2C1,因此反馈系数 F F F与起振时间 t 起 振 时 间 t_{起振时间} t起振时间呈现负相关,而与振荡频率呈现正相关
负载电阻 R L R_L RL 对起振时间,输出电压幅值的影响
增大负载电阻RL,观测、记录输出电压的波形,并说明负载增大对起振时间、输出电压幅度的影响。
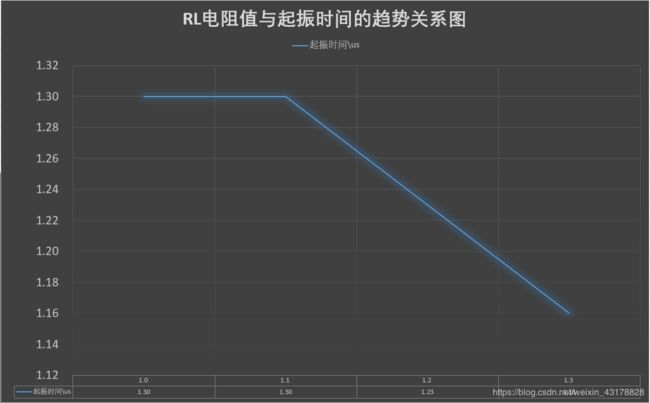
- R L = 1.1 k Ω R_L=1.1k\Omega RL=1.1kΩ
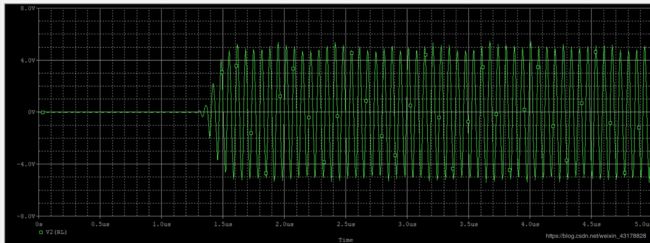

V C P P = 4.83 V V_{CPP}=4.83V VCPP=4.83V
t 起 振 时 间 = 1.3 u s t_{起振时间}=1.3us t起振时间=1.3us
- R L = 1.2 k Ω R_L=1.2k\Omega RL=1.2kΩ


V C P P = 5.82 V V_{CPP}=5.82V VCPP=5.82V
t 起 振 时 间 = 1.23 u s t_{起振时间}=1.23us t起振时间=1.23us
- R L = 1.3 k Ω R_L=1.3k\Omega RL=1.3kΩ

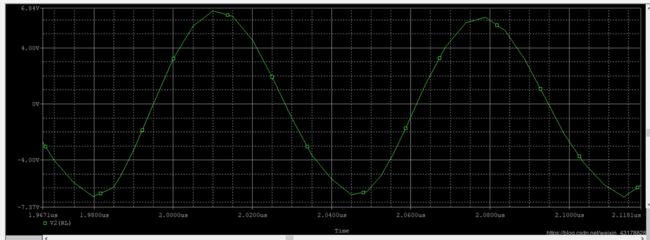
V C P P = 6.53 V V_{CPP}=6.53V VCPP=6.53V
t 起 振 时 间 = 1.16 u s t_{起振时间}=1.16us t起振时间=1.16us
因此,在一定范围内, R L R_{L} RL与 V C P P V_{CPP} VCPP呈现正相关关系,同时与 t 起 振 时 间 t_{起振时间} t起振时间呈现负相关关系
另外值得注意的是,当 R L R_L RL上升到一定程度,波形会发生削底失真。