【leetcode】122.买卖股票的最佳时机 II (五种方法开阔思路!java实现)
122. 买卖股票的最佳时机 II
难度简单
给定一个数组,它的第 i 个元素是一支给定股票第 i 天的价格。
设计一个算法来计算你所能获取的最大利润。你可以尽可能地完成更多的交易(多次买卖一支股票)。
**注意:**你不能同时参与多笔交易(你必须在再次购买前出售掉之前的股票)。
示例 1:
输入: [7,1,5,3,6,4]
输出: 7
解释: 在第 2 天(股票价格 = 1)的时候买入,在第 3 天(股票价格 = 5)的时候卖出, 这笔交易所能获得利润 = 5-1 = 4 。
随后,在第 4 天(股票价格 = 3)的时候买入,在第 5 天(股票价格 = 6)的时候卖出, 这笔交易所能获得利润 = 6-3 = 3 。
示例 2:
输入: [1,2,3,4,5]
输出: 4
解释: 在第 1 天(股票价格 = 1)的时候买入,在第 5 天 (股票价格 = 5)的时候卖出, 这笔交易所能获得利润 = 5-1 = 4 。
注意你不能在第 1 天和第 2 天接连购买股票,之后再将它们卖出。
因为这样属于同时参与了多笔交易,你必须在再次购买前出售掉之前的股票。
示例 3:
输入: [7,6,4,3,1]
输出: 0
解释: 在这种情况下, 没有交易完成, 所以最大利润为 0。
提示:
1 <= prices.length <= 3 * 10 ^ 40 <= prices[i] <= 10 ^ 4
方法一:暴力搜索
我是最后写搜索算法的,但是把它放在了开头,意思是想告诉自己:搜索算法应该是最先想到的。
可能暴力搜索不能让有些面试官满意,但是我觉得有些不拘一格面试官会认可你先说出搜索的算法这个思路,然后再以搜索算法为起点,考虑更好的算法。
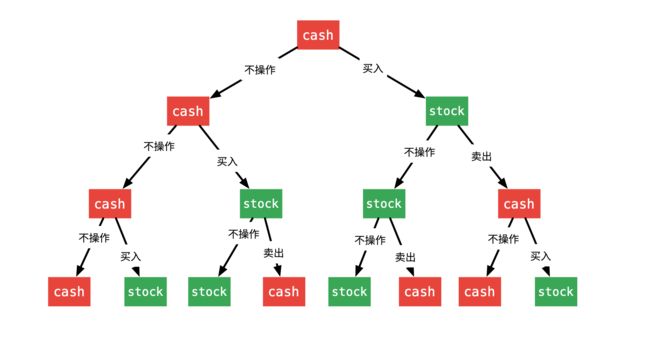
根据题意:因为不限制交易次数,在每一天,我就可以根据当前是否持有股票选择相应的操作。“暴力搜索” 也叫 “回溯搜索”、“回溯法”,首先画出树形图。
下面编写代码:
参考代码 1:
- Java
public class Solution {
private int res;
public int maxProfit(int[] prices) {
int len = prices.length;
if (len < 2) {
return 0;
}
this.res = 0;
dfs(prices, 0, len, 0, res);
return this.res;
}
/**
* @param prices 股价数组
* @param index 当前是第几天,从 0 开始
* @param status 0 表示不持有股票,1表示持有股票,
* @param profit 当前收益
*/
private void dfs(int[] prices, int index, int len, int status, int profit) {
if (index == len) {
this.res = Math.max(this.res, profit);
return;
}
dfs(prices, index + 1, len, status, profit);
if (status == 0) {
// 可以尝试转向 1
dfs(prices, index + 1, len, 1, profit - prices[index]);
} else {
// 此时 status == 1,可以尝试转向 0
dfs(prices, index + 1, len, 0, profit + prices[index]);
}
}
}
class Solution {
public int maxProfit(int[] prices) {
return calculate(prices, 0);
}
public int calculate(int prices[], int s) {
if (s >= prices.length)
return 0;
int max = 0;
for (int start = s; start < prices.length; start++) {
int maxprofit = 0;
for (int i = start + 1; i < prices.length; i++) {
if (prices[start] < prices[i]) {
int profit = calculate(prices, i + 1) + prices[i] - prices[start];
if (profit > maxprofit)
maxprofit = profit;
}
}
if (maxprofit > max)
max = maxprofit;
}
return max;
}
}
复杂度分析
- 时间复杂度: O ( n n ) O(n^n) O(nn),调用递归函数 n n n^n nn 次。
- 空间复杂度:O(n),递归的深度为 n。
很显然,超时在意料之中。注意看这个超时是在数据规模很大的时候,因此,可以说明搜索算法是正确的。
事实上,写完搜索算法,状态转移基本上就已经能够思考清楚了,不过我们还是先来看看贪心算法吧。
方法二:贪心算法
这道题使用贪心算法的流程是这样的:
- 从第
i天(这里i >= 1)开始,与第i - 1的股价进行比较,如果股价有上升(严格上升),就将升高的股价(prices[i] - prices[i- 1])记入总利润,按照这种算法,得到的结果就是符合题意的最大利润。
下面对这个算法进行几点说明:
1、该算法仅可以用于计算,但计算的过程并不是真正交易的过程,但可以用贪心算法计算题目要求的最大利润。下面说明这个等价性:以 [1, 2, 3, 4] 为例,这 4 天的股价依次上升,按照贪心算法,得到的最大利润是:
- Java
res = (prices[3] - prices[2]) + (prices[2] - prices[1]) + (prices[1] - prices[0])
= prices[3] - prices[0]
仔细观察上面的式子,按照贪心算法,在索引为 1、2、3 的这三天,我们做的操作应该是买进昨天的,卖出今天的,虽然这种操作题目并不允许,但是它等价于:“在索引为 0 的那一天买入,在索引为 3 的那一天卖出”。
2、解释一下它为什么叫 “贪心算法”
我们还是回到贪心算法的定义:(下面是来自《算法导论(第三版)》第 16 章的叙述)
“贪心算法” 在每一步总是做出在当前看来最好的选择。
因此,
- “贪心算法” 和 “动态规划”、“回溯搜索” 算法一样,完成一件事情,是分步决策的;
- “贪心算法” 在每一步总是做出在当前看来最好的选择,我是这样理解 “最好” 这两个字的意思:
- “最好” 的意思往往根据题目而来,可能是 “最小”,也可能是 “最大”;
- 贪心算法和动态规划相比,它既不看前面(也就是说它不需要从前面的状态转移过来),也不看后面(无后效性,后面的选择不会对前面的选择有影响),因此贪心算法时间复杂度一般是线性的,空间复杂度是常数级别的。
- 这道题 “贪心” 的地方在于,对于 “今天的股价 - 昨天的股价”,得到的结果有 3 种可能:(1)正数(2)
0(3)负数。
贪心算法的决策是:只加正数。
参考代码 2:
- Java
public class Solution {
public int maxProfit(int[] prices) {
int res = 0;
int len = prices.length;
for (int i = 0; i < len - 1; i++) {
int diff = prices[i + 1] - prices[i];
if (diff > 0) {
res += diff;
}
}
return res;
}
}
复杂度分析:
- 时间复杂度:O(N),这里 N 表示股价数组的长度;
- 空间复杂度:O(1)。
等价写法:
参考代码 3:
Java 代码:
public class Solution {
public int maxProfit(int[] prices) {
int res = 0;
int len = prices.length;
for (int i = 0; i < len - 1; i++) {
res += Math.max(prices[i + 1] - prices[i], 0);
}
return res;
}
}
复杂度分析:(同上)
下面证明 “贪心算法” 的有效性。
我们借助 “差分” 这个概念,可以证明 “贪心算法” 的有效性。贪心算法就是选择那些所有差分(严格)大于 0 的数,把它们相加即可。
使用反证法:假设 “贪心算法” 得到的解并不是最优解,即我们还能够找到一个可行解比 “贪心算法” 得到的利润还多。差分数组中除了差分为正数的项以外,还有就是差分为 0 的项与差分为负数的项。“贪心算法” 是所有差分为正数的项的和。
1、如果可行解在 “贪心算法” 的基础上,选择了差分为 0 的项,得到的结果与“贪心算法”得到的结果一样,因此加上差分为 0 的项不会比“贪心算法”得到的结果更好;
2、如果可行解在 “贪心算法” 的基础上,选择了差分为负数的项,加上一个负数得到的结果一定比 “贪心算法” 得到的结果要少,加上差分为负数的项,一定比 “贪心算法” 得到的结果更少;
3、如果可行解在 “贪心算法” 的基础上,去掉了任何一个差分为正数的项,同上,得到的结果一定比 “贪心算法” 得到的结果要小,因此,“贪心算法” 的所有组成项不能删去任何一个。
综上,除了 “贪心算法” 以外,找不到一个更优的解法,因此 “贪心算法” 就是最优解。(证完)
方法三:动态规划
想到动态规划的原因是:可以用贪心算法解决的问题,一般情况下都可以用动态规划。因此,不妨从 “状态”、“状态转移方程” 的角度考虑一下,使用动态规划的思路解决这道问题。
根据 「力扣」第 121 题的思路,需要设置一个二维矩阵表示状态。
第 1 步:定义状态
状态 dp[i][j] 定义如下
- 第一维
i表示索引为i的那一天(具有前缀性质,即考虑了之前天数的收益)能获得的最大利润; - 第二维
j表示索引为i的那一天是持有股票,还是持有现金。这里0表示持有现金(cash),1表示持有股票(stock)。
第 2 步:思考状态转移方程
- 状态从持有现金(cash)开始,到最后一天我们关心的状态依然是持有现金(cash);
- 每一天状态可以转移,也可以不动。状态转移用下图表示:
(状态转移方程写在代码中)
说明:
- 因为不限制交易次数,除了最后一天,每一天的状态可能不变化,也可能转移;
- 写代码的时候,可以不用对最后一天单独处理,输出最后一天,状态为
0的时候的值即可。
第 3 步:确定起始
起始的时候:
- 如果什么都不做,
dp[0][0] = 0; - 如果买入股票,当前收益是负数,即
dp[0][1] = -prices[i];
第 4 步:确定终止
终止的时候,上面也分析了,输出 dp[len - 1][0],因为一定有 dp[len - 1][0] > dp[len - 1][1]。
参考代码 4:
- Java
public class Solution {
public int maxProfit(int[] prices) {
int len = prices.length;
if (len < 2) {
return 0;
}
// 0:持有现金
// 1:持有股票
// 状态转移:0 → 1 → 0 → 1 → 0 → 1 → 0
int[][] dp = new int[len][2];
dp[0][0] = 0;
dp[0][1] = -prices[0];
for (int i = 1; i < len; i++) {
// 这两行调换顺序也是可以的
dp[i][0] = Math.max(dp[i - 1][0], dp[i - 1][1] + prices[i]);
dp[i][1] = Math.max(dp[i - 1][1], dp[i - 1][0] - prices[i]);
}
return dp[len - 1][0];
}
}
复杂度分析:
- 时间复杂度:O(N),这里 N 表示股价数组的长度。
- 空间复杂度:O(N),虽然是二维数组,但是第二维是常数,与问题规模无关。
我们也可以将状态数组分开设置,语义更明确。
参考代码 5:
public class Solution {
public int maxProfit(int[] prices) {
int len = prices.length;
if (len < 2) {
return 0;
}
// cash:持有现金
// hold:持有股票
// 状态数组
// 状态转移:cash → hold → cash → hold → cash → hold → cash
int[] cash = new int[len];
int[] hold = new int[len];
cash[0] = 0;
hold[0] = -prices[0];
for (int i = 1; i < len; i++) {
// 这两行调换顺序也是可以的
cash[i] = Math.max(cash[i - 1], hold[i - 1] + prices[i]);
hold[i] = Math.max(hold[i - 1], cash[i - 1] - prices[i]);
}
return cash[len - 1];
}
}
复杂度分析:(同上)
第 5 步:考虑状态压缩
由于当前行只参考上一行,每一行就 2 个值,因此可以考虑使用“滚动变量”(“滚动数组”技巧)。
参考代码 6:
- Java
public class Solution {
public int maxProfit(int[] prices) {
int len = prices.length;
if (len < 2) {
return 0;
}
// cash:持有现金
// hold:持有股票
// 状态转移:cash → hold → cash → hold → cash → hold → cash
int cash = 0;
int hold = -prices[0];
int preCash = cash;
int preHold = hold;
for (int i = 1; i < len; i++) {
cash = Math.max(preCash, preHold + prices[i]);
hold = Math.max(preHold, preCash - prices[i]);
preCash = cash;
preHold = hold;
}
return cash;
}
}
复杂度分析:
- 时间复杂度:O(N),这里 N 表示股价数组的长度。
- 空间复杂度:O(1),分别使用两个滚动变量,将一维数组状态压缩到常数。
方法五:峰谷法
算法
假设给定的数组为:
[7, 1, 5, 3, 6, 4]
如果我们在图表上绘制给定数组中的数字,我们将会得到:
![]()
如果我们分析图表,那么我们的兴趣点是连续的峰和谷。
用数学语言描述为:
T o t a l P r o f i t = ∑ i ( h e i g h t ( p e a k i ) − h e i g h t ( v a l l e y i ) ) Total Profit= \sum_{i}(height(peak_i)-height(valley_i)) TotalProfit=∑i(height(peaki)−height(valleyi))
关键是我们需要考虑到紧跟谷的每一个峰值以最大化利润。如果我们试图跳过其中一个峰值来获取更多利润,那么我们最终将失去其中一笔交易中获得的利润,从而导致总利润的降低。
例如,在上述情况下,如果我们跳过 p e a k i peak_i peaki和 v a l l e y j valley_j valleyj试图通过考虑差异较大的点以获取更多的利润,获得的净利润总是会小与包含它们而获得的净利润,因为 C总是小于 A+B。
- Java
class Solution {
public int maxProfit(int[] prices) {
int i = 0;
int valley = prices[0];
int peak = prices[0];
int maxprofit = 0;
while (i < prices.length - 1) {
while (i < prices.length - 1 && prices[i] >= prices[i + 1])
i++;
valley = prices[i];
while (i < prices.length - 1 && prices[i] <= prices[i + 1])
i++;
peak = prices[i];
maxprofit += peak - valley;
}
return maxprofit;
}
}
复杂度分析
- 时间复杂度:O(n)。遍历一次。
- 空间复杂度:O(1)。需要常量的空间。