最大流应用问题(深大算法实验6)报告+代码
所有实验的资源
链接: https://pan.baidu.com/s/1lukZRM3Rsd1la35EyyJcvg
提取码: iv72
目录
- 写在前面
- 问题描述
- 图构建:
- 图最大流的求解:
- Ford-Fulkerson方法的伪代码描述:
- Edmonds-karp算法
- 几个技巧与实现细节:
- Edmonds-karp算法:复杂度分析
- Dinic算法
- Dinic:复杂度分析
- 引入当前弧优化:
- Dinic+当前弧优化:复杂度分析
- 引入多路增广策略:
- 多路增广Dinic:复杂度分析
- ISAP
- ISAP复杂度分析
- 预流推进算法
- 预流推进伪代码描述
- 最高标号预流推进
- 算法测试
- 时间测试
- EK
- Dinic:
- Dinic+当前弧优化
- Dinic+多路增广
- ISAP
- 最高标号预流推进
- 结论:
- 总览:
- 数据测试:结论
- 总结:
- 代码
写在前面
期末终于算法课快要完结了。
这学期算法课可谓是最难顶的课程了,又正好是线上上课,提问互动的机会相对较少,老师上课抛砖引玉,实验内容又比较难,我花了大部分的时间在找算法,实现算法,改算法bug上。
我也参考过很多往届师兄的报告,但是大多都比较抽象晦涩,而且没有代码只讲方法,比较难以理解具体实现的细节。
所以我打算记录一下自己的报告+代码,前人coding后人copying ,希望让大家少走弯路。。。
注意:不要直接copy代码,这是冲塔行为!查重系统鲨疯辣。
问题描述
图构建:
基本图
值班问题可以抽象为图,每个医生是一个节点,每个假日也是一个节点,医生和假日之间有路径表示该医生可以在这个假日值班

加上虚拟的源点和汇点,组成一张“流网络”,表示所有值班的可能性

看似求解这个流网络的最大流就能解决问题,值得注意的是这个网络并不能很好的描述这个实验的问题,因为这个实验有三个限制:
1. 要使得每一个假日都有医生值班
2. 每个医生值班不得超过c日
3. 每人每个假期最多值班一天
所以我们的图要加上相应的限制:引入“限流节点”与“限流边”
限流节点:对每个医生的每个假期都虚拟一个限流节点(图中的x医生的x假期),而每个医生最多给每个假期分配1流量,表示每个医生每个假期只能值班一天
限流边:我们给每个医生的流量为c,因为每个医生最多值班c天,此外,每个假日给到汇点的流量都为1(下图最右边黑色边),表示每个假日一个人值班就够了,防止出现多人值班同一天的冲突
图最大流的求解:
Ford-Fulkerson方法与Edmonds-karp算法
回退边与增广图
假设现在有一条边A->B权值是10,这意味着A可以向B发送10流量

现在A只发送了8流量,那么A还可以发送2流量,此时边的权值变为2

这时候因为B接收了8流量,B可以选择退货,即有回退边B->A权值为8,表示B可以向A发送8流量,即退货,我们可以得知,A->B发送x流量,那么A->B的权值-=x,B->A的权值+=x
 增广图是把所有的回退边都当成原图的有向边,在原图的基础上增加回退边而形成的一种图
增广图是把所有的回退边都当成原图的有向边,在原图的基础上增加回退边而形成的一种图


Ford-Fulkerson方法的伪代码描述:
 这里的最短增广路径指的是经过的节点最少,而不是边权值之和最小
这里的最短增广路径指的是经过的节点最少,而不是边权值之和最小
Edmonds-karp算法
Ford-Fulkerson方法之所以称为方法就是因为没有确定找最短增广路径的方法,但是Edmonds-karp算法则实例化了这种方法,即使用bfs求取最短增广路径,因为bfs一旦搜索到,那么经过的节点必定是最少的
几个技巧与实现细节:
- Bfs需要拥有返回值,如果没有搜索到汇点,返回false,否则返回true
- 需要不停bfs直到不存在增广路(即bfs返回false)
- 我们可以通过边bfs边建立并查集,方便后面查找最短增广路径。搜索到汇点之后,沿着汇点一路沿着并查集的生成树走到源点即是路径
- 最小流量可以使用一个数组 min_flow[x] 表示从源点到x点的最小流量,假设x点有邻居y,那么y最小流量的推导为:min_flow[y] = min(xy边的权值, min_flow[x])
Edmonds-karp算法:复杂度分析
n为顶点数目 e为边数目
每次bfs需要O(e)的复杂度,而总共需要进行f次bfs图流量才达到饱和,总共复杂度为O(ef),而f的值为n*e
下面给出证明,f的值为n*e:
每次增广路径都会导致一条边满载,也就是一条边被“移除”,但是要想再次经过这条边,那么必须是从它的反向边经过了,而从反向边经过会导致路径的长度至少增加2,而最短增广路径总路程不超过n,所以最多有n/2条经过该边的路径,每条边最多被更新 n/2 次

一共有e条边,总共的增广次数就是 n/2 * e 即需要花费 O(ne)次,而每次寻找增广路径bfs需要O(e),所以复杂度O(ne2)
Dinic算法
与EK算法类似,dinic算法同样选择最短增广路径并且更新,不同的是,dinic采用bfs分层dfs的方式,使得一次搜索可以更新多条增广路上的权值,大大提升速度

Dfs沿着层次进行:
沿着xy方向进行dfs当且仅当x的层次+1 == y的层次,保证dfs找到的都是最短增广路。
一旦找到终点,路径即是最短,退栈的同时更新边的权值即可
Dinic算法:伪代码描述
代码使用递归定义,分配flow流量给x节点,并且让x节点尝试向下分发流量,返回值是x实际分发的流量

dfs递归退栈后,重新bfs建立层次关系,然后再次dfs递归调用直到bfs无法找到汇点

Dinic:复杂度分析
因为dinic的dfs按照层次来递归,因为每次扫描出的层数是递增的,而且不超过n,所以外循环bfs最多进行n次,而因为每次找增广路都有一条边作为“瓶颈”,一共有e条边,就有e个瓶颈,e条路径,要进行e次dfs(这里的dfs需要访问控制数组vis,每个节点最多访问一次),每次dfs复杂度为O(e),总体复杂度为O(ne2)
引入当前弧优化:
因为dfs一旦找到就返回,而一次bfs分层可能存在很多条相同长度的增广路,那么会在同一张图上跑多次dfs,而图不断更新,可用的边越来越少,我们试图跳过前面已经走过的“死路”,直接从未访问的路开始走。

当前弧优化:伪代码实现
实现很简单,用cur_arc[x]表示x节点未访问的边在邻接表中的起始下标

Dinic+当前弧优化:复杂度分析
因为一共e条边,而不管做多少次dfs,因为减少了对死路的判断,保证每次邻接表第一个邻居就是能走的活路,所以每次dfs走n步一定能够走到目标而不必回退,dfs的开销由O(e)变为O(n),而因为最多有e条路径,dfs需要最多做e次,所以每一轮的代价是O(ne),而因为外循环的bfs分层最多进行n次,所以总的代价是O(n2e)
Ps. 百度百科上面的Dinic正是用这种当前弧优化 才使得复杂度维持在O(n2e)
引入多路增广策略:
如下图所示,普通dinic算法找到之后,直接全部退出,而多路增广优化的Dinuc算法找到之后,回溯到父节点,然后继续向下搜索,最后退栈的时候再更新边的权值,这样一次dfs可以进行多次更新

多路增广Dinic:伪代码描述

和普通dinic算法不同,多路增广优化的dinic,每次bfs分层后只需要调用一次dfs即可

多路增广Dinic:复杂度分析
外循环同样是每次bfs扫描层次,最多做n次bfs(原因同上普通Dinic算法的复杂度分析)
而每次内循环都做一次dfs,需要注意这里的dfs不带访问控制数组,只要有边就能过,这意味着每一个节点可以多次被经过,所以dfs复杂度不是O(e)
因为最多存在e条最短增广路径,而每次走到汇点至多走n步,所以dfs的代价是O(ne),这使得多路增广Dinic的总体复杂度是O(n2e)
ISAP
和Dinic算法类似,同为增广路算法,不像Dinic算法每次dfs之后都要bfs重新建立层次关系,ISAP在dfs的同时就动态地更新节点的层次关系,减少bfs的次数,将dfs利用到极致
。
ISAP算法只需要一次bfs建立最初的层次关系。除此之外,ISAP算法还引入了“gap”优化,即如果某一高度的节点数目为0,直接判断没有路径并且结束搜索。因为按层次bfs保证层次是严格连续下降的,如果某一高度节点数目为0表示出现断层,无法到达。

我们只需一次bfs,然后一直dfs直到flag为true表示断层出现,或者源点高度>=n,因为两者都表示不存在增广路径能够到达汇点
ISAP复杂度分析
和Dinic算法中的dfs一样,复杂度是O(ne),原因也是不带访问控制数组,一个节点会被多次访问,最多有e条增广路径,而每次需要走过n个点到达汇点,所以复杂度O(ne),因为外循环需要判断源点的高度,而源点最多增高n次,总体复杂度为O(n2e)
预流推进算法
上面提及的算法都是增广路算法,即按照增广路径不断压入少量的流量,直到满流,而预流推进算法则是一次性将巨额流量压入网络,如果能够流就让他流,即将流量转到下一个节点,否则就溢出,不管溢出的部分。

超流量与活跃节点
引入超流量概念,这个概念表示某个节点当前状态下能够分发出去多少流量,超流量随着算法的迭代而不停更新。
如果一个节点的超流量大于0,我们称之为活跃节点,因为他存在分配流量的可能
流量的更新
F单位的流量从x点流向y点,我们称之为更新流量,即x的超流量-=F 同时y的超流量+=F
标号与重新标号
标号也就是节点的高度(层次),调整一个节点的高度的行为,我们称之为重新标号,节点的高度调整公式为:level[x] = min(level[x的邻居])+1
预流推进伪代码描述
我们用hyper_flow[]数组记录每个节点的超流量,注意实际代码中,relabel前还要判断x是否是汇点,如果是汇点就不管,除此之外relabel如果未发现邻居就将高度设置为inf,推流时加上访问控制数组
最高标号预流推进
将普通预流推进算法中的队列换成依据节点高度排序的优先队列(堆)即可。
最高标号预流推进:复杂度分析
查阅资料可知该算法的复杂度被证明为O(n2 * sqrt(e))
算法测试
假设有3名医生,2个假期,每个假日3天假日,每人最多值班2天,按照上文提及的规则,随机生成的图如下:
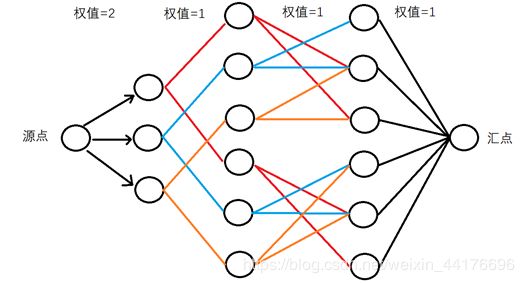
将算法结束后的图中,有装载流量的边都打印出来,得到答案图:

医生值班问题的分配方案如下

时间测试
EK
Dinic:
Dinic+当前弧优化
Dinic+多路增广
ISAP
最高标号预流推进
结论:
可以看到,在四个影响问题的因素中,【医生个数】【假期个数】【假日个数】对时间复杂度的影响是明显的,因为他们影响着图的规模。而【最大值班天数】对问题无影响,曲线随测试时间误差与随机数据而波动。
总览:
将问题量化为有x个医生,x个假期,每个假期x个假日,每个医生随机选取每个假期的x/2(向上取整)个假日,作为可以值班的假日,生成随机图并且计算最大流
对x取不同的值以计算,得出的结果对比如下


可以看到EK算法需要的时间远超其他算法,我们去除EK算法再次画图

可以看到EK算法是最慢的,虽然Dinic算法和EK算法复杂度相同,但是实际随机数据的测试中效果远远好于EK算法。而两种改进的Dinic算法中,多路增广Dinic算法比当前弧优化效果要好。最快的算法是ISAP,因为其省去bfs的代价而且有gap优化。而最高标号预流推进算法虽然理论效率最高,但复杂度上限卡的紧,实际效果差强人意。
数据测试:结论
复杂度:
EK = Dinic > 多路增广Dinic = 当前弧Dinic = ISAP > 最高标号预流推进
实际用时:
EK > Dinic > 当前弧Dinic > 最高标号预流推进 > 多路增广Dinic > ISAP
总结:
从几种增广路径方法可以看出,图的遍历是解决很多图问题的基础
从原图生成增广图,其实可以只用生成一次,然后直接在增广图上进行操作与修改,不用每次都修改原图再生成增广图
Dfs搜索的时候应当注意邻接条件,比如边的权值不能为0或者点是否被访问,两种算法使用不同的dfs策略要注意区分
应该使用邻接表而不是邻接矩阵存储,因为邻接表下的算法时间复杂度低
最高标号预流推进中用到的堆结构,可以直接用STL的优先队列实现
代码
#include
ans += flow;
vector<int> path;
while(y!=src) // 沿着生成树找起点并沿途更新边
{
path.push_back(y);
x = father[y];
for(i=0; i<adj[x].size(); i++) if(edges[adj[x][i]].ed==y) break;
edges[adj[x][i]].val -= flow;
edges[edges[adj[x][i]].pair].val += flow; // 更新另一半的边
y = x;
}
/*
path.push_back(y);
for(int i=path.size()-1; i>=0; i--) cout<
}
/*
* @function EK : Edmonds-Karp算法求最大流
*/
void EK()
{
ans = 0;
while(1)
{
if(!bfs_augment()) break;
graph_update();
/*
// 打印图信息
for(int i=0; i "<}
//cout<<"最大流:"<
}
/* ---------------------------------------------------------------------------- */
/*
* @function bfs_level : 层次遍历标记节点层数
* @param : ----
* @return ;如果找到终点return true 否则false
* @explain : ----
*/
bool bfs_level()
{
for(int i=0; i<n; i++) level[i]=-1;
level[src] = 0; // 起始节点第0层
queue<int> q; q.push(src);
int lv = 0; // bfs层次数
while(!q.empty())
{
lv++;
int qs = q.size();
for(int sq=0; sq<qs; sq++)
{
int x=q.front(),y; q.pop();
if(x==dst) return true;
for(int i=0; i<adj[x].size(); i++)
{
edge e = edges[adj[x][i]];
y = e.ed;
if(level[y]!=-1 || e.val==0) continue;
level[y] = lv;
q.push(y);
}
}
}
return false;
}
/*
void dfs_dinic(int x, list& path)
{
father[x] = 1; // father充当访问控制数组
for(int i=0; i
/*
* @function dfs_dinic1 : 普通Dinic算法 往x节点塞入flow流量 并且尝试分配下去
* @param x : 当前节点
* @param flow : 要向x分配多少流量(最大可用值)
* @return : 节点x实际向下分配了多少流量
* @explain : 一旦找到立即返回 一次找一条
* : 使用father数组作为访问控制visit数组
*/
int dfs_dinic1(int x, int flow)
{
father[x] = 1;
if(x==dst) return flow;
for(int i=0; i<adj[x].size(); i++)
{
edge e = edges[adj[x][i]];
int y = e.ed;
if(e.val==0 || level[y]!=level[x]+1 || father[y]==1) continue;
int res = dfs_dinic1(y, min(flow, e.val));
edges[adj[x][i]].val-=res, edges[edges[adj[x][i]].pair].val+=res;
if(res!=0) return res; // 找到直接返回
}
return 0; // 没找到则返回0
}
/*
* @function Dinic1 : 普通Dinic算法求最大流
* @explain : 用level数组做层次标记数组 层次逐渐增加
*/
void Dinic1()
{
ans = 0;
while(bfs_level())
{
while(1)
{
for(int i=0; i<n; i++) father[i]=0;
int res = dfs_dinic1(src, inf);
if(res==0) break; // 找不到增广路 需要重新bfs更新层次
ans += res;
}
/*
// 打印图信息
for(int i=0; i "<}
//cout<<"最大流:"<
}
/*
* @function dfs_dinic2 : Dinic + 当前弧优化
* @param x : 当前节点
* @param flow : 要向x分配多少流量(最大可用值)
* @return : 节点x实际向下分配了多少流量
* @explain : 一旦找到立即返回 一次找一条
* : 使用father数组作为访问控制visit数组
*/
int dfs_dinic2(int x, int flow)
{
father[x] = 1;
if(x==dst) return flow;
for(int& i=cur_arc[x]; i<adj[x].size(); i++)
{
edge e = edges[adj[x][i]];
int y = e.ed;
if(e.val==0 || level[y]!=level[x]+1 || father[y]==1) continue;
int res = dfs_dinic2(y, min(flow, e.val));
edges[adj[x][i]].val-=res, edges[edges[adj[x][i]].pair].val+=res;
if(res!=0) return res; // 找到直接返回
}
return 0; // 没找到则返回0
}
/*
* @function Dinic2 : Dinic + 当前弧优化
* @explain : 用level数组做层次标记数组 层次逐渐增加
*/
void Dinic2()
{
ans = 0;
while(bfs_level())
{
// 当前弧重置
for(int i=0; i<n; i++) cur_arc[i]=0;
while(1)
{
for(int i=0; i<n; i++) father[i]=0; // 每次dfs更新visit数组
int res = dfs_dinic2(src, inf);
if(res==0) break; // 找不到增广路 需要重新bfs更新层次
ans += res;
}
/*
// 打印图信息
for(int i=0; i "<}
//cout<<"最大流:"<
}
/*
* @function dfs_dinic1 : Dinic + 多路增广
* @param x : 当前节点
* @param flow : 要向x分配多少流量(最大可用值)
* @return : 节点x实际向下分配了多少流量
* @explain : 一次找完所有路径
*/
int dfs_dinic3(int x, int flow)
{
if(x==dst) return flow;
int temp_flow = flow; // 记录能分配的最大值
for(int i=0; i<adj[x].size(); i++)
{
edge e = edges[adj[x][i]];
int y = e.ed;
if(e.val==0 || level[y]!=level[x]+1) continue;
int res = dfs_dinic3(y, min(flow, e.val));
edges[adj[x][i]].val-=res, edges[edges[adj[x][i]].pair].val+=res;
flow-=res; // 更新可用流量
if(flow==0) return temp_flow; // 如果分完了就结束
}
return temp_flow-flow; // 返回实际分配的
}
/*
* @function Dinic1 : Dinic算法 + 多路增广
* @explain : 用level数组做层次标记数组 层次逐渐增加
*/
void Dinic3()
{
ans = 0;
while(bfs_level())
{
ans += dfs_dinic3(src, inf); // dfs层次图以更新边
/*
// 打印图信息
for(int i=0; i "<}
//cout<<"最大流:"<
}
/* ---------------------------------------------------------------------------- */
/*
* @function dfs_ISAP : 在层次图中向下分配流量 往x节点塞入flow流量 并且尝试分配下去
* @param x : 当前节点
* @param flow : 要向x分配多少流量(最大可用值)
* @return : 节点x实际向下分配了多少流量
* @explain : 和Dinic类似 只是边bfs边更新层次
*/
bool ISAP_flag = false;
int dfs_ISAP(int x, int flow)
{
if(x==dst) return flow;
int temp_flow = flow; // temp_flow保存这个点拥有的流量
for(int i=0; i<adj[x].size(); i++)
{
edge e = edges[adj[x][i]];
int y = e.ed;
if(level[x]!=level[y]+1 || e.val==0) continue;
int res = dfs_ISAP(y, min(e.val, flow));
edges[adj[x][i]].val-=res, edges[edges[adj[x][i]].pair].val+=res; // 退栈时更新图
flow -= res; // 分配了res流量给某个分支
if(flow==0) return temp_flow; // 分配完了则返回
}
dis_cnt[level[x]]--; // 计算新距离计数
if(dis_cnt[level[x]]==0) ISAP_flag=true; // 出现断层就提前结束
level[x]++; // 已经分配完所子节点 不存在和刚一样长度增广路径 路径长度严格连续增加
dis_cnt[level[x]]++; // 计算新距离计数
return temp_flow-flow; // 返回已经分配的流量数目
}
/*
* @function ISAP : ISAP
* @explain : 用level数组做距离标记数组,距离逐渐减少
: 引入当前弧优化和gap优化
*/
void ISAP()
{
bfs_level();
// 层次数组变为距离数组
int mlv = *max_element(level.begin(), level.end());
for(int i=0; i<n; i++) level[i]=mlv-level[i], dis_cnt[i]=0;
// 距离计数数组计算初始值
for(int i=0; i<n; i++) dis_cnt[level[i]]++;
ans=0; ISAP_flag=false;
while(level[src]<n && !ISAP_flag)
{
ans+=dfs_ISAP(src, inf);
if(ISAP_flag) break;
}
/*
// 打印图信息
for(int i=0; i "<//cout<<"最大流:"<
}
/* ---------------------------------------------------------------------------- */
typedef struct hlpp_node
{
int x, h;
hlpp_node(int a, int b){x=a; h=b;}
bool operator < (const hlpp_node& n2)const{return h<n2.h;}
}hlpp_node;
/*
* @function relabel : 重新标记高度
* @param x : 重新标记x点的高度 高度为邻接点之中最低的+1
* @return : ----
*/
void relabel(int x)
{
level[x] = inf;
for(int i=0; i<adj[x].size(); i++)
{
if(edges[adj[x][i]].val==0) continue;
level[x] = min(level[x], level[edges[adj[x][i]].ed]+1);
}
}
/*
* @function HLPP : 最高标号预流推进
* @param : ----
* @return : ----
* @explain : 时间复杂度上界为 O(n^2 * sqrt(e)) 卡的比较紧
*/
void HLPP()
{
bfs_level();
// 层次数组变为距离数组
int mlv = *max_element(level.begin(), level.end());
for(int i=0; i<n; i++) level[i]=mlv-level[i], dis_cnt[i]=0, hyper_flow[i]=0;
vector<int> vis(n);
priority_queue<hlpp_node> q; q.push(hlpp_node(src, level[src]));
hyper_flow[src] = inf; // 源点无限流量
vis[src] = 1;
while(!q.empty())
{
hlpp_node tp=q.top(); q.pop();
int x=tp.x, h=tp.h;
if(hyper_flow[x]==0) continue; // 如果流量为0直接出队
for(int i=0; i<adj[x].size(); i++)
{
edge e = edges[adj[x][i]];
int y = e.ed;
if(level[x]!=level[y]+1 || e.val==0) continue;
int flow = min(hyper_flow[x], e.val);
hyper_flow[x]-=flow, hyper_flow[y]+=flow; // 更新超额流量
edges[adj[x][i]].val-=flow, edges[edges[adj[x][i]].pair].val+=flow; // 更新图
if(y!=src && y!=dst && !vis[y]) q.push(hlpp_node(y, level[y])),vis[y]=1;// 不是源目点,则继续流出
if(hyper_flow[x]==0) break; // 流完了则退出
}
// 如果流量有剩余 则抬高 x 以便更多的流出 如果高过源点则回流 不再处理
if(hyper_flow[x]>0 && x!=dst && level[x]<n)
{
relabel(x); // 抬高 如果无邻居则高度设为 inf
q.push(hlpp_node(x, level[x])); // 试图再次流出
}
}
ans = hyper_flow[dst];
/*
// 打印图信息
for(int i=0; i "<//cout<<"最大流:"<
}
/* ---------------------------------------------------------------------------- */
/*
* @function add_edge : 添加一条边及其反向边
* @param st : 正向边起点
* @param ed : 正向边终点
* @param val : 边的权值(最大允许流量
*/
void add_edge(int st, int ed, int val)
{
int ii=edges_.size();
edges_.push_back(edge(st, ed, val, ii+1));
edges_.push_back(edge(ed, st, 0, ii));
adj[st].push_back(ii); adj[ed].push_back(ii+1);
}
/*
* @function load_random_graph : 随机生成图
* @param doc_num : 医生数目 doctor number
* @param hol_num : 假期数目 holiday number
* @param day_num : 每个假期包含的假日数目 day number
* @param c : 每个医生最多值班c天
*/
void load_random_graph(int doc_num, int hol_num, int day_num, int c)
{
int st, ed;
n = 1 + doc_num + doc_num*hol_num + hol_num*day_num + 1;
cout<<n<<endl;
adj.resize(n);
father.resize(n);
min_flow.resize(n);
level.resize(n);
cur_arc.resize(n);
dis_cnt.resize(n+1);
hyper_flow.resize(n);
edges_.clear();
edges.clear();
src=0, dst=n-1;
for(int i=1; i<doc_num+1; i++)
{
st=src, ed=i;
add_edge(st, ed, c);
}
for(int i=1; i<doc_num+1; i++)
{
for(int j=0; j<hol_num; j++)
{
st=i, ed=1+doc_num+doc_num*j+(i-1);
add_edge(st, ed, 1);
st=ed;
vector<int> select(day_num);
for(int k=0; k<day_num/2+1; k++)
{
int id = rand()%day_num;
// id = k; // 冲突测试用
if(select[id]==1){k--; continue;}
select[id] = 1;
ed = 1+doc_num+doc_num*hol_num+day_num*j+id;
add_edge(st, ed, 1);
}
}
}
for(int i=0; i<hol_num*day_num; i++)
{
st=1+doc_num+doc_num*hol_num+i, ed=dst;
add_edge(st, ed, 1);
}
e = edges_.size();
edges.resize(e);
}
/*
* @function re_graph : 将图恢复为默认生成的图
*/
void re_graph()
{
for(int i=0; i<e; i++) edges[i]=edges_[i];
}
void cin_graph()
{
cin>>n>>e>>src>>dst;
adj.resize(n);
father.resize(n);
min_flow.resize(n);
level.resize(n);
cur_arc.resize(n);
dis_cnt.resize(n+1);
hyper_flow.resize(n);
for(int i=0; i<e; i++)
{
int st, ed, limit; cin>>st>>ed>>limit;
add_edge(st, ed, limit);
}
e = edges_.size();
edges.resize(e);
}
int main()
{
//cin_graph();
/*
re_graph(); // 打印图信息
for(int i=0; i "<double t1=0, t2=0, t3=0, t4=0, t5=0, t6=0;
clock_t st,ed;
#define BATCH 10
#define SIZE_G 30
int batch = BATCH;
load_random_graph(SIZE_G, SIZE_G, SIZE_G, SIZE_G);
while(batch--)
{
cout<<"数据生成完毕:"<<batch<<endl;
re_graph();
st = clock();
EK();
ed = clock();
t1 += (double)(ed-st)/CLOCKS_PER_SEC;
re_graph();
st = clock();
Dinic1();
ed = clock();
t2 += (double)(ed-st)/CLOCKS_PER_SEC;
re_graph();
st = clock();
Dinic2();
ed = clock();
t3 += (double)(ed-st)/CLOCKS_PER_SEC;
re_graph();
st = clock();
Dinic3();
ed = clock();
t4 += (double)(ed-st)/CLOCKS_PER_SEC;
re_graph();
st = clock();
ISAP();
ed = clock();
t5 += (double)(ed-st)/CLOCKS_PER_SEC;
re_graph();
st = clock();
HLPP();
ed = clock();
t6 += (double)(ed-st)/CLOCKS_PER_SEC;
//re_graph(); EK();
//re_graph(); Dinic1(); // 普通dinic
//re_graph(); Dinic2(); // Dinic+当前弧优化
//re_graph(); Dinic3(); // Dinic+多路增广
//re_graph(); ISAP();
//re_graph(); HLPP();
}
cout<<t1/BATCH<<endl;
cout<<t2/BATCH<<endl;
cout<<t3/BATCH<<endl;
cout<<t4/BATCH<<endl;
cout<<t5/BATCH<<endl;
cout<<t6/BATCH<<endl;
return 0;
}
/*
6 7 0 5
0 2 2
0 1 2
1 4 1
2 4 5
2 3 2
3 5 1
4 5 2
7 11 0 6
0 1 3
0 3 3
1 2 4
2 0 3
2 3 1
2 4 2
3 4 2
3 5 6
4 1 1
4 6 1
5 6 9
*/























