PTA 乙级2020春季题解

第一次参加$pat$，报个乙级练练手(其实就是对于自己的英语水平毫无自信)，(总共用时一个半小时，有点小菜，最后一题$debug$了久了一点)。

第一题：

7-1 对称日 (15分)

央视新闻发了一条微博，指出 2020 年有个罕见的“对称日”，即 2020 年 2 月 2 日，按照 年年年年月月日日 格式组成的字符串 20200202 是完全对称的。

给定任意一个日期，本题就请你写程序判断一下，这是不是一个对称日？

输入格式：

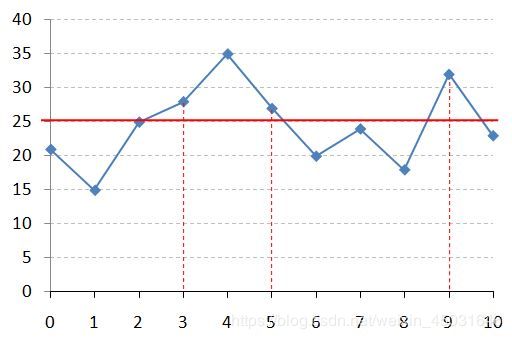
输入首先在第一行给出正整数 N（1

一月：Jan
二月：Feb
三月：Mar
四月：Apr
五月：May
六月：Jun
七月：Jul
八月：Aug
九月：Sep
十月：Oct
十一月：Nov
十二月：Dec
Day 是月份中的日期，为 [1, 31] 区间内的整数；Year 是年份，为 [1, 9999] 区间内的整数。

输出格式：

对每一个给定的日期，在一行中先输出 Y 如果这是一个对称日，否则输出 N；随后空一格，输出日期对应的 年年年年月月日日 格式组成的字符串。

输入样例：

5
Feb 2, 2020
Mar 7, 2020
Oct 10, 101
Nov 21, 1211
Dec 29, 1229

输出样例：

Y 20200202
N 20200307
Y 01011010
Y 12111121
N 12291229

思路：

就是把年月日全部化成字符串的形式，然后翻转一下，看看是不是一样然后输出$Y,N$，判断月份的时候有很多种方法，但是还是$if$最简单粗暴。

#include 
using namespace std;
string get(int x, int tmp) {
    string s = "";
    for (int i = 0; i < tmp; i++) {
        int t = x % 10;
        x /= 10;
        s += (char)(t + '0');
    }
    reverse(s.begin(), s.end());
    return s;
}
int main() {
    int t; cin >> t;
    while (t--) {
        string month;
        int day, year;
        cin >> month;
        scanf("%d, %d", &day, &year);
        int mo = 0;
        if (month == "Jan") mo = 1;
        if (month == "Feb") mo = 2;
        if (month == "Mar") mo = 3;
        if (month == "Apr") mo = 4;
        if (month == "May") mo = 5;
        if (month == "Jun") mo = 6;
        if (month == "Jul") mo = 7;
        if (month == "Aug") mo = 8;
        if (month == "Sep") mo = 9;
        if (month == "Oct") mo = 10;
        if (month == "Nov") mo = 11;
        if (month == "Dec") mo = 12;
        string ss = get(year, 4) + get(mo, 2) + get(day, 2);
        string s = ss;
        reverse(s.begin(), s.end());
        if (ss == s) {
            cout << "Y " << ss << endl;
        } else {
            cout << "N " << ss << endl;
        }
    }
}

第二题：

7-2 超标区间 (20分)

上图是用某科学研究中采集的数据绘制成的折线图，其中红色横线表示正常数据的阈值（在此图中阈值是 25）。你的任务就是把超出阈值的非正常数据所在的区间找出来。例如上图中横轴 [3, 5] 区间中的 3 个数据点超标，横轴上点 9 （可以表示为区间 [9, 9]）对应的数据点也超标。

输入格式：

输入第一行给出两个正整数 N（≤10⁴）和 T（≤100），分别是数据点的数量和阈值。第二行给出 N 个数据点的纵坐标，均为不超过 1000 的正整数，对应的横坐标为整数 0 到 N−1。

输出格式：

按从左到右的顺序输出超标数据的区间，每个区间占一行，格式为 [A, B]，其中 A 和 B 为区间的左右端点。如果没有数据超标，则在一行中输出所有数据的最大值。

输入样例 1：

11 25
21 15 25 28 35 27 20 24 18 32 23

输出样例 1：

[3, 5]
[9, 9]

输入样例 2：

11 40
21 15 25 28 35 27 20 24 18 32 23

输出样例 2：

35

思路：

对于每一次的值判断是否超出阈值，如果超出就有两种情况：

• 前面未出现过连续的超出阈值的，那么此时这个就是第一个，然后用$last$纪律 这个开头的位置
• 前面出现过连续的超出阈值的，那么不做处理

如果不超出的话，那么也有两种情况：

• 前面的连续的是超出阈值的，那么此时到这个就停止了，然后输出区间
• 如果连续的未超出阈值，那么不做处理

需要注意的是最后的时候，如果最后一个是超出阈值，我们就要当作第$n+1$个不超过阈值来计算。

#include 
using namespace std;
const int maxn = 1e4 + 10;
int a[maxn] = {0};
int main() {
    int n, t, Max = 0;
    cin >> n >> t;
    for (int i = 0; i < n; i++) cin >> a[i];
    int last = -1;
    bool flag = false;
    for (int i = 0; i < n; i++) {
        Max = max(a[i], Max);
        if (a[i] > t && last == -1)  {
            last = i;
        } else if (a[i] <= t && last != -1) {
            printf("[%d, %d]\n", last, i - 1);
            last = -1;
            flag = true;
        }
    }
    if (last != -1) printf("[%d, %d]\n", last, n - 1);
    else if (!flag) printf("%d\n", Max);
}

第三题

7-3 钱串子的加法 (20分)

人类习惯用 10 进制，可能因为大多数人类有 10 根手指头，可以用于计数。这个世界上有一种叫“钱串子”（学名“蚰蜒”）的生物，有 30 只细长的手/脚，在它们的世界里，数字应该是 30 进制的。本题就请你实现钱串子世界里的加法运算。

输入格式：

输入在一行中给出两个钱串子世界里的非负整数，其间以空格分隔。

所谓“钱串子世界里的整数”是一个 30 进制的数字，其数字 0 到 9 跟人类世界的整数一致，数字 10 到 29 用小写英文字母 a 到 t 顺次表示。

输入给出的两个整数都不超过 10⁵位。

输出格式：

在一行中输出两个整数的和。注意结果数字不得有前导零。

输入样例：

2g50ttaq 0st9hk381

输出样例：

11feik2ir

思路：

实际上就是将字符串转换成数字，然后对于每一个位子相加，最后按照$30$进制来计算，最后的时候，在转换回去，需要注意的前导零的问题，最后需要将前导零全部删除。

#include 
using namespace std;
const int maxn = 1e5 + 10;
string s, t;
int cnt[maxn], tot = 0;
int getnum(char c) {
    int t = 0;
    if (c >= 'a' && c <= 't') t = c - 'a' + 10;
    else t = c - '0';
    return t;
}
int main() {
    cin >> s >> t;
    int lens = s.size(), lent = t.size();
    int carry = 0;
    reverse(s.begin(), s.end());
    reverse(t.begin(), t.end());
    for (int i = 0; i < max(lens, lent); i++) {
        int ss, st;
        if (i >= lens) ss = 0;
        else ss = getnum(s[i]);
        if (i >= lent) st = 0;
        else st = getnum(t[i]);
        //cout << ss << " " << st << endl;
        int num = ss + st + carry;
        carry = num / 30;
        num %= 30;
        cnt[tot++] = num;
    }
    if (carry != 0) cnt[tot++] = carry;
    int k = tot - 1;
    for (int i = tot - 1; i >= 0; i--) {
        if (cnt[i] == 0) k--;
        else break;
    }
    if (k == -1) k = 0;
    for (int i = k; i >= 0; i--) {
        if (cnt[i] < 10) cout << cnt[i];
        else cout << char(cnt[i] - 10 + 'a');
    }
    cout << endl;
}

第四题：

7-4 全素日 (20分)

以上图片来自新浪微博，展示了一个非常酷的“全素日”：2019年5月23日。即不仅20190523本身是个素数，它的任何以末尾数字3结尾的子串都是素数。

本题就请你写个程序判断一个给定日期是否是“全素日”。

输入格式：

输入按照 yyyymmdd 的格式给出一个日期。题目保证日期在0001年1月1日到9999年12月31日之间。

输出格式：

从原始日期开始，按照子串长度递减的顺序，每行首先输出一个子串和一个空格，然后输出 Yes，如果该子串对应的数字是一个素数，否则输出 No。如果这个日期是一个全素日，则在最后一行输出 All Prime!。

输入样例 1：

20190523

输出样例 1：

20190523 Yes
0190523 Yes
190523 Yes
90523 Yes
0523 Yes
523 Yes
23 Yes
3 Yes
All Prime!

输入样例 2：

20191231

输出样例 2：

20191231 Yes
0191231 Yes
191231 Yes
91231 No
1231 Yes
231 No
31 Yes
1 No

思路：

对于输入的话，可以用字符串输入和整数输入，现在想想整数应该会更简单一点，因为不用转换，对于每一个的整数，可以直接用朴素判定方法就行了，然后字符串的话，那么每次减少一位，整数的话，直接除零。

#include 
using namespace std;
const int maxn = 1e5 + 10;
bool is_prime(int n) {
    if (n == 1 || n == 0) return false;
    for (int i = 2; i <= sqrt(n); i++) {
        if (n % i == 0) return false;
    }
    return true;
}
int getnum(string s, int st) {
    int tmp = 0;
    for (int i = st; i < s.size(); i++) {
        tmp = tmp * 10 + s[i] - '0';
        cout << s[i];
    }
    return tmp;
}
string s;
int main() {
    cin >> s;
    int cnt = 0;
    for (int i = 0; i < s.size(); i++) {
        int t = getnum(s, i);
        if (is_prime(t) == true) {
            cout << " Yes\n";
            cnt++;
        } else cout << " No\n";
    }
    if (cnt == s.size()) cout << "All Prime!\n";
    return 0;
}

第五題：

7-5 裁判机 (25分)

有一种数字游戏的规则如下：首先由裁判给定两个不同的正整数，然后参加游戏的几个人轮流给出正整数。要求给出的数字必须是前面已经出现的某两个正整数之差，且不能等于之前的任何一个数。游戏一直持续若干轮，中间有写重复或写错的人就出局。

本题要求你实现这个游戏的裁判机，自动判断每位游戏者给出的数字是否合法，以及最后的赢家。

输入格式：

输入在第一行中给出 2 个初始的正整数，保证都在 [1,10⁵] 范围内且不相同。

第二行依次给出参加比赛的人数 N（2≤N≤10）和每个人都要经历的轮次数 M（2≤M≤10³）。

以下 N 行，每行给出 M 个正整数。第 i 行对应第 i 个人给出的数字（i=1,⋯,N）。游戏顺序是从第 1 个人给出第 1 个数字开始，每人顺次在第 1 轮给出自己的第 1 个数字；然后每人顺次在第 2 轮给出自己的第 2 个数字，以此类推。

输出格式：

如果在第 k 轮，第 i 个人出局，就在一行中输出 Round #k: i is out.。出局人后面给出的数字不算；同一轮出局的人按编号增序输出。直到最后一轮结束，在一行中输出 Winner(s): W1 W2 … Wn，其中 W1 … Wn 是最后的赢家编号，按增序输出。数字间以 1 个空格分隔，行末不得有多余空格。如果没有赢家，则输出 No winner.。

输入样例 1：

101 42
4 5
59 34 67 9 7
17 9 8 50 7
25 92 43 26 37
76 51 1 41 40

输出样例 1：

Round #4: 1 is out.
Round #5: 3 is out.
Winner(s): 2 4

输入样例 2：

42 101
4 5
59 34 67 9 7
17 9 18 50 49
25 92 58 1 39
102 32 2 6 41

输出样例 2：

Round #1: 4 is out.
Round #3: 2 is out.
Round #4: 1 is out.
Round #5: 3 is out.
No winner.

思路：

我们设置三个数组$isminu,isper,book$分别代表着差值判定，人是否出局，数字是否曾经出现。
如果这题使用暴力的话，那么时间复杂度应该是$O(m^{2}n)$，在数据范围下，是不会超时的，然后就是判定

• 首先判断是否出局，因为出局后的数字不算
• 第二个判定是因为题目的数据只是给出了前两个正整数的，我不知道包不包括后面的，如果数字过大，就会数组越界，但是经过验证，数据应该都是在$10^5$内的。
• 第三个就是判断数字是不是之前的时候出现过。
• 第四个判断就是数字是否是两个的差。
• 最后就是如果都能通过的话，那么就再用一个循环，计算出全部的差值，用数组记录。

需要注意的时候，刚开始的两个数字的差值和数字记得用数组记录，差值记录了，但是数字忘记了，然后$debug$了好久。

其实这题有一些问题(个人看法)，题目说出局人后面给出的数字不算，但是此时的数字并没有说明是否有效，刚开始的时候我就认为此时是有效的后面的无效，然后就是数据问题。

#include 
using namespace std;
const int maxn = 1e5 + 10;
vector<int> v;
bool isminu[maxn] = {false}, isper[maxn] = {false}, book[maxn] = {false};
int a[20][1010];
int main() {
    int num1, num2;
    scanf("%d %d", &num1, &num2);
    v.push_back(num1), v.push_back(num2);
    book[num1] = book[num2] = true;
    isminu[abs(num1 - num2)] = true;
    int n, m;
    scanf("%d %d", &n, &m);
    for (int i = 1; i <= n; i++) {
        for (int j = 1; j <= m; j++) {
            scanf("%d", &a[i][j]);
        }
    }
    for (int j = 1; j <= m; j++) {
        for (int i = 1; i <= n; i++) {
            //cout << i << " " << j << " " << isminu[76] << endl;
            if (isper[i] == true) continue;
            if (a[i][j] >= max(num1, num2)) {
                printf("Round #%d: %d is out.\n", j, i);
                isper[i] = true;
                continue;
            }
            if (book[a[i][j]] == true) {
                printf("Round #%d: %d is out.\n", j, i);
                isper[i] = true;
                continue;
            }
            book[a[i][j]] = true;
            if (isminu[a[i][j]] == false) {
                printf("Round #%d: %d is out.\n", j, i);
                isper[i] = true;
                continue;
            }
            for (int k = 0; k < v.size(); k++) {
                isminu[abs(a[i][j] - v[k])] = true;
            }
            v.push_back(a[i][j]);
        }
    }
    bool flag = false;
    for (int i = 1; i <= n; i++) {
        if (isper[i] == false) {
            flag = true;
            break;
        }
    }
    if (!flag) cout << "No winner.\n";
    else {
        printf("Winner(s):");
        for (int i = 1; i <= n; i++) {
            if (isper[i] == false) cout << " " << i;
        }
    }
    return 0;
}