【排序算法】基数排序:LSD 与 MSD
基数排序是通过“分配”和“收集”过程来实现排序。
1)分配,先从个位开始,根据位值(0-9)分别放到0~9号桶中(比如53,个位为3,则放入3号桶中)
2)收集,再将放置在0~9号桶中的数据按顺序放到数组中
重复(1)(2)过程,从个位到最高位(比如32位无符号整形最大数4294967296,最高位10位)。而这个思想该如何理解呢?请看以下例子。
(1)假设有欲排数据序列如下所示:
73 28 93 43 55 14 22 65 26 81
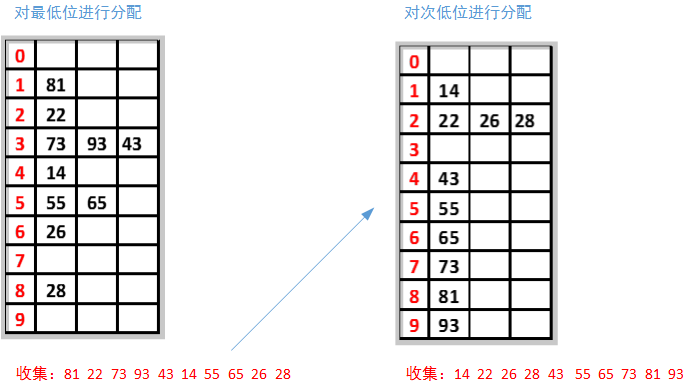
首先根据个位数的数值,在遍历数据时将它们各自分配到编号0至9的桶(个位数值与桶号一一对应)中。
从低位到高位分配收集过程:
观察可以看到,此时原无序数据序列已经排序完毕。如果排序的数据序列有三位数以上的数据,则重复进行以上的动作直至最高位数为止。
基于两种不同的排序顺序,我们将基数排序分为
LSD(Least significant digital):排序方式由数值的最右边(低位)开始
MSD(Most significant digital):由数值的最左边(高位)开始。
注意一点:
LSD的基数排序适用于位数少的数列,如果位数多的话,使用MSD的效率会比较好。
MSD的方式由高位数为基底开始进行分配,但在分配之后并不马上合并回一个数组中,而是在每个“桶子”中建立“子桶”,将每个桶子中的数值按照下一数位的值分配到“子桶”中。在进行完最低位数的分配后再合并回单一的数组中。
由高位到低位分配收集过程:
73 28 93 43 55 14 22 65 26 81
(2)我们把扑克牌的排序看成由花色和面值两个数据项组成的主关键字排序。要求如下:
花色顺序:梅花<方块<红心<黑桃
面值顺序:2<3<4<...<10
那么,若要将一副扑克牌排成下列次序:
梅花2,...,梅花A,方块2,...,方块A,红心2,...,红心A,黑桃2,...,黑桃A。
有两种排序方法:
<1>先按花色分成四堆,把各堆收集起来;然后对每堆按面值由小到大排列,再按花色从小到大按堆收叠起来。----称为"最高位优先"(MSD)法。
<2>先按面值由小到大排列成13堆,然后从小到大收集起来;再按花色不同分成四堆,最后顺序收集起来。----称为"最低位优先"(LSD)法。
2.算法分析
平均时间复杂度:O(dn)(d即表示整形的最高位数)
空间复杂度:O(10n) (10表示0~9,用于存储临时的序列)
稳定性:稳定
3.程序实现
(1)LSD法实现
最低位优先法首先依据最低位关键码Kd对所有对象进行一趟排序,
再依据次低位关键码Kd-1对上一趟排序的结果再排序,
依次重复,直到依据关键码K1最后一趟排序完成,就可以得到一个有序的序列。
使用这种排序方法对每一个关键码进行排序时,不需要再分组,而是整个对象组。
因为分配和收集阶段,数字符合先入先出的关系。因此可以用10个队列来保存 0-9 上分配的数字,在收集阶段,按先入先出的顺序取出每个桶中的数字,依次放到原数组中。
/********************************************************
*函数名称:GetNumInPos
*参数说明:num 一个整形数据
* pos 表示要获得的整形的第pos位数据
*说明: 找到num的从低到高的第pos位的数据
*********************************************************/
int GetNumInPos(int num, int pos)
{
int temp = 1;
for (int i = 0; i < pos - 1; i++)
temp *= 10;
return (num / temp) % 10;
}
#define MAXPOS 10 //最高位的位数
void RadixSort(vector &A)
{
int len = A.size();
vector> radixArray(10); //分为0~9的序列空间
for (int pos = 1; pos <= MAXPOS; pos++) //从个位开始到最高位数
{
for (int i = 0; i < len; i++) //分配过程
{
int num = GetNumInPos(A[i], pos);
radixArray[num].push_back(A[i]);
}
for (int i = 0, j = 0; i < 10; i++) //收集
{
while (!radixArray[i].empty())
{
A[j++] = radixArray[i].front(); //取首部数据依次插入原数组
radixArray[i].erase(radixArray[i].begin()); //移除首部元素
}
}
}
} 最高位优先法通常是一个递归的过程:
<1>先根据最高位关键码K1排序,得到若干对象组,对象组中每个对象都有相同关键码K1。
<2>再分别对每组中对象根据关键码K2进行排序,按K2值的不同,再分成若干个更小的子组,每个子组中的对象具有相同的K1和K2值。
<3>依此重复,直到对关键码Kd完成排序为止。
<4> 最后,把所有子组中的对象依次连接起来,就得到一个有序的对象序列。
/********************************************************
*函数名称:GetNumInPos
*参数说明:num 一个整形数据
* pos 表示要获得的整形的第pos位数据
*说明: 找到num的从低到高的第pos位的数据
*********************************************************/
int GetNumInPos(int num, int pos)
{
int temp = 1;
for (int i = 0; i < pos - 1; i++)
temp *= 10; return (num / temp) % 10;
}
//MSD,调用时指定最高位数d
void RadixSort(vector &A, int d)
{
int len = A.size();
vector> radixArray(10); //分为0~9的序列空间,用队列保存每个桶分配的数据 //位数大于0,且数组长度大于1
if (d >= 1 && len > 1)
{
for (int i = 0; i < len; i++) //分配过程
{
int num = GetNumInPos(A[i], d);
radixArray[num].push_back(A[i]);
}
cout << endl;
for (int i = 0, j = 0; i < 10; i++) //收集
{
RadixSort(radixArray[i], d-1); //递归,对每个子桶从次高位开始分配
while (!radixArray[i].empty())
{
A[j++] = radixArray[i].front(); //取队列首部数据依次插入原数组
radixArray[i].erase(radixArray[i].begin());
}
}
}
}
参考:http://blog.csdn.net/cjf_iceking/article/details/7943609
http://www.cnblogs.com/Braveliu/archive/2013/01/21/2870201.html