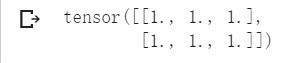第一次作业：深度学习基础

【第一部分】视频学习心得及问题总结

绪论

什么是人工智能？

       人工智能是使一个机器像人一样进行感知、认知、决策、执行的人工程序或系统。

图灵测试：假设在一个封闭空间中，完成一个任务，外部人员能否判断出完成这个任务的是机器还是人。

人工智能三个层面：计算智能（能存能算）、感知智能（能听会说，能看会认）、认知智能（能理解，会思考）。

知识工程：

       1.基于手工设计规则建立专家系统

       2.结果容易解释

       3.系统构建费时费力

       4.依赖专家主观经验，难以保证一致性和准确性

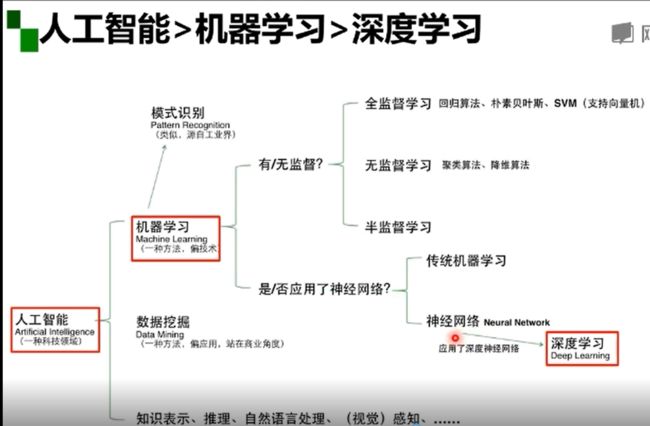
机器学习

       1.基于数据自动学习

       2.减少人工复杂工作，但结果可能不易解释

       3.提高信息处理的效率，且准确率较高

       4.来源于真实数据，减少人工规则主观性，可信度高

机器学习三要素：模型、策略、算法。

       模型：对要学习问题映射的假设（问题模型，确定假设空间）

       策略：从假设空间中学习、选择最优模型的准则（确定目标函数）

       算法：根据目标函数求解最优模型的具体计算方法（求解模型参数）

      模型分类：

              数据标记（监督学习、无监督学习、半监督学习、强化学习）

              数据分布（参数模型，非参数模型）

              建模对象（判别模型、生成模型）

监督学习模型：输入样本具有标记，从数据中学习标记分界面，适用于预测数据标记

 

 

 

 深度学习只是机器学习的一种， 机器学习是实现人工智能的一种手段。

 

深度学习三个助推剂：数据、算法、计算力

深度学习的“不能”

      1.算法不稳定，容易被攻击；

      2.模型复杂度高，难以纠错和调试；

      3.模型层级复合程度高，参数不透明；

      4.端到端训练方式对数据依赖性强，模型增量性差；当样本数据量小的时候，深度学习无法体现强大拟合能力；深度学习可以进行语义标注和关系检测，但无法进一步完成图像描述；

      5.专注直观感知类问题，对开放性推理问题无能为力；

      6.人类知识无法有效引入进行监督，机器偏见难以避免

浅层神经网络

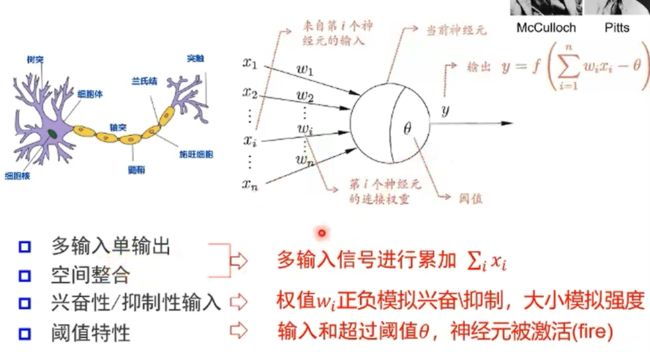
神经元特性：多输入单输出；空间整合和时间整合；兴奋性输入和抑制性输入；阈值特性。

M-P神经元：

 

 激活函数举例：

单层感知器：通过非线性激活函数，可以实现简单的逻辑非、与、或操作（线性问题），但却不可以解决异或问题（非线性问题）。

多层感知器：通过加隐层将一个非线性问题转化为线性问题。

万有逼近定理

如果一个隐层包含足够多的神经元，三层前馈网络（输入-隐层-输出）能任意精度逼近任意预定的连续函数。

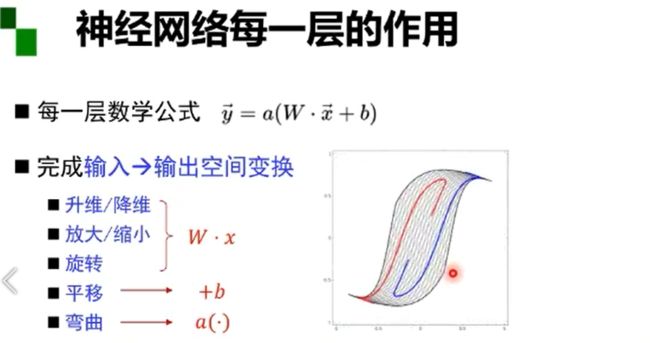
利用矩阵的线性变换和激活函数的非线性变换，将原始输入空间投影到线性可分的空间去分类/回归。

双层感知器逼近非连续函数。当隐层足够宽时，双隐层感知器可以逼近任意非连续函数，可解决任何复杂的分类问题。

 

 

 

 

 

数据训练就是为了让神经网络选择这样一种线性和非线性变换

增加节点：增加维度，即增加线性转换能力

增加层数：增加激活函数的次数，即增加非线性转换次数

在神经元总数相当的情况下，增加网络深度可比增加宽度带来更强的网络表示能力：产生更多地线性区域。深度的贡献是指数增长的，而宽度的贡献是线性的。

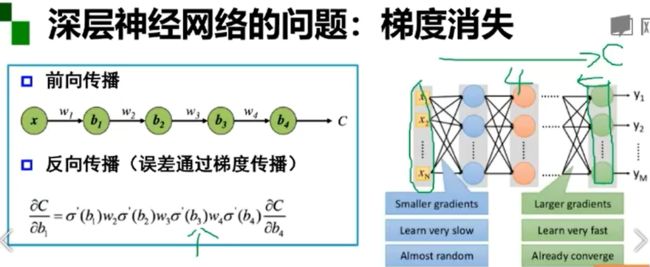
神经网络的参数学习：误差法向传播

 

 

 

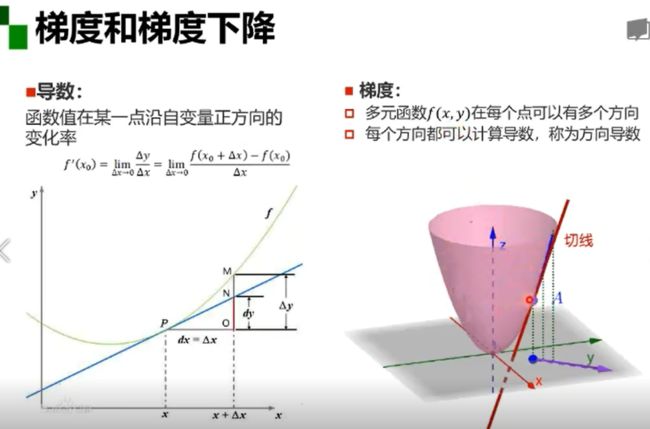
梯度与梯度下降

 

 

 

梯度：某一函数在该点处的方向导数沿着该方向取得最大值

梯度下降：是一种无约束优化方法，参数沿着负梯度方向更新可以使函数值下降，可能无法找到全局的极值点，而是找到局部极值点。

梯度消失问题

误差无法传播，参数过小，只更新了最后一层参数，前面的参数没有更新

 

1.当激活函数（sigmoid）落在饱和区的时候，其导数会很小，从而导致整个链式求导的反向传播的值很小，接近于零；从而在反向传播过程中，最后几层网络的训练效果很好，但前面的网络层因为梯度消失原因得不到很好的训练，从而在有新的训练输入后，经过前面的网络层，使得数据混乱，导致最后几层的训练失去效果

2.增加深度会造成梯度消失，误差无法传播

3.多层网络容易陷入局部极值，难以训练

 

自编码器

 

 

 受限玻尔兹曼机

 

 

 自编码器vs受限玻尔兹曼机

 

 

 

 

【第二部分】代码练习

2.1 图像处理基本练习

1.下载并显示图像

!wget https://raw.githubusercontent.com/summitgao/ImageGallery/master/yeast_colony_array.jpg

import matplotlib
import numpy as np
import matplotlib.pyplot as plt

import skimage
from skimage import data
from skimage import io

#colony = io.imread('yeast_colony_array.jpg')
#print(type(colony))
#print(colony.shape)

# Plot all channels of a real image
plt.subplot(121)
plt.imshow(colony[:,:,:])
plt.title('3-channel image')
plt.axis('off')

# Plot one channel only
plt.subplot(122)
plt.imshow(colony[:,:,0])
plt.title('1-channel image')
plt.axis('off');

2.读取并改变图像像素值

# Get the pixel value at row 10, column 10 on the 10th row and 20th column
camera = data.camera()
print(camera[10, 20])

# Set a region to black
camera[30:100, 10:100] = 0
plt.imshow(camera, 'gray')

 

发现图中camera[30:100, 10:100] = 0的区域改变了颜色

# Set the first ten lines to black
camera = data.camera()
camera[:10] = 0
plt.imshow(camera, 'gray')

纵坐标为10 的值全部的一行改变了颜色

 

 

# Set to "white" (255) pixels where mask is True
camera = data.camera()
mask = camera < 80
camera[mask] = 255
plt.imshow(camera, 'gray')

 

 mask = camera < 80, mask是一个bool数组，维度(512 x 512)，与图片像素对应。图片中像素值大于80的位置对应的mask数组的值为False，其余为True。

 

 

 

# Set brighter pixels to red
red_cat = cat.copy()
reddish = cat[:, :, 0] > 160
red_cat[reddish] = [255, 0, 0]
plt.imshow(red_cat)

 

 

 图片R(RGB)通道的像素值大于160的位置对应的reddish数组的值为True，其余为False，下一句代码将相应位置变为红色。

 

# Change RGB color to BGR for openCV
BGR_cat = cat[:, :, ::-1]
plt.imshow(BGR_cat)

将最后一维数据顺序反转，最后一维的形式是[r,g,b],倒序后即[b,g,r]。

 

 

上述两张图片是改变通道的数值来实现对于图像色彩处理。

 3.转换图像数据类型

skimage.img_as_float(img)--- [64-float]
skimage.img_as_ubyte(i1. mg)--- [8-unit]
skimage.img_as_uint(img)--- [16-unit]
skimage.img_as_int(img)--- [16-int]

4.绘制图像直方图

img = data.camera()
plt.hist(img.ravel(), bins=256, histtype='step', color='black');

其中ravel使用了降维

 

 

5.图像分割

# Use colony image for segmentation
colony = io.imread('yeast_colony_array.jpg')

# Plot histogram
img = skimage.color.rgb2gray(colony)
plt.hist(img.ravel(), bins=256, histtype='step', color='black');

skimage.color.rgb2gray(img):RGB图像转灰度图像。

 

 

 6.Canny算子用来进行边缘检测

img_edges = canny(img)：边缘检测
img_filled = ndi.binary_fill_holes(img_edges)：填充二进制图像矩阵中的孔洞。

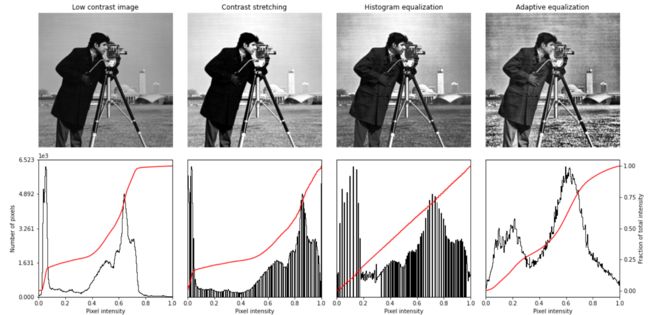
 7.改变图像的对比度

# Contrast stretching

p2, p98 = np.percentile(img, (2, 98))

img_rescale = skimage.exposure.rescale_intensity(img, in_range=(p2, p98))

plt.imshow(img_rescale, 'gray')

 

# Equalization
img_eq = skimage.exposure.equalize_hist(img)
plt.imshow(img_eq, 'gray')

 

# Adaptive Equalization
img_adapteq = skimage.exposure.equalize_adapthist(img, clip_limit=0.03)
plt.imshow(img_adapteq, 'gray')

 

# Display results
def plot_img_and_hist(img, axes, bins=256):
    """Plot an image along with its histogram and cumulative histogram.

    """
    img = img_as_float(img)
    ax_img, ax_hist = axes
    ax_cdf = ax_hist.twinx()

    # Display image
    ax_img.imshow(img, cmap=plt.cm.gray)
    ax_img.set_axis_off()
    ax_img.set_adjustable('box')

    # Display histogram
    ax_hist.hist(img.ravel(), bins=bins, histtype='step', color='black')
    ax_hist.ticklabel_format(axis='y', style='scientific', scilimits=(0, 0))
    ax_hist.set_xlabel('Pixel intensity')
    ax_hist.set_xlim(0, 1)
    ax_hist.set_yticks([])

    # Display cumulative distribution
    img_cdf, bins = skimage.exposure.cumulative_distribution(img, bins)
    ax_cdf.plot(bins, img_cdf, 'r')
    ax_cdf.set_yticks([])

    return ax_img, ax_hist, ax_cdf

fig = plt.figure(figsize=(16, 8))
axes = np.zeros((2, 4), dtype=np.object)
axes[0, 0] = fig.add_subplot(2, 4, 1)
for i in range(1, 4):
    axes[0, i] = fig.add_subplot(2, 4, 1+i, sharex=axes[0,0], sharey=axes[0,0])
for i in range(0, 4):
    axes[1, i] = fig.add_subplot(2, 4, 5+i)

ax_img, ax_hist, ax_cdf = plot_img_and_hist(img, axes[:, 0])
ax_img.set_title('Low contrast image')

y_min, y_max = ax_hist.get_ylim()
ax_hist.set_ylabel('Number of pixels')
ax_hist.set_yticks(np.linspace(0, y_max, 5))

ax_img, ax_hist, ax_cdf = plot_img_and_hist(img_rescale, axes[:, 1])
ax_img.set_title('Contrast stretching')

ax_img, ax_hist, ax_cdf = plot_img_and_hist(img_eq, axes[:, 2])
ax_img.set_title('Histogram equalization')

ax_img, ax_hist, ax_cdf = plot_img_and_hist(img_adapteq, axes[:, 3])
ax_img.set_title('Adaptive equalization')

ax_cdf.set_ylabel('Fraction of total intensity')
ax_cdf.set_yticks(np.linspace(0, 1, 5))

fig.tight_layout()
plt.show()

 

 

2.2 pytorch基础练习

# 可以是一维数组（向量）
x = torch.tensor([1,2,3,4,5,6])
print(x)

 

 

 

# 可以是二维数组（矩阵）
x = torch.ones(2,3)
print(x)

 

 

 

# 可以是任意维度的数组（张量）
x = torch.ones(2,3,4)
print(x)

 

 

 

 

 

# 创建一个 2x4 的tensor
m = torch.Tensor([[2, 5, 3, 7],
                  [4, 2, 1, 9]])

print(m.size(0), m.size(1), m.size(), sep=' -- ')

   表示这个tensor的size 中第一个是2 ，第二个是4

 

 

 

 此处在开始运行的时候是错误的，原因是m和v一个是float型一个是整形，无法进行运算，于是我在step=1改成了step=1.使得v也变为float型，最终m@v的结果是float型。

 

 

 

 

两个矩阵进行拼接：

# 创建两个 1x4 的tensor
a = torch.Tensor([[1, 2, 3, 4]])
b = torch.Tensor([[5, 6, 7, 8]])

# 在 0 方向拼接 （即在 Y 方各上拼接）, 会得到 2x4 的矩阵
print( torch.cat((a,b), 0))

 

 

# 在 1 方向拼接 （即在 X 方各上拼接）, 会得到 1x8 的矩阵
print( torch.cat((a,b), 1))

 

 

2.3 螺旋数据分类

#数据初始化
import random
import torch
from torch import nn, optim
import math
from IPython import display
from plot_lib import plot_data, plot_model, set_default

# 因为colab是支持GPU的，torch 将在 GPU 上运行
device = torch.device("cuda:0" if torch.cuda.is_available() else "cpu")

# 初始化随机数种子。神经网络的参数都是随机初始化的，
# 不同的初始化参数往往会导致不同的结果，当得到比较好的结果时我们通常希望这个结果是可以复现的，
# 因此，在pytorch中，通过设置随机数种子也可以达到这个目的
seed = 12345
random.seed(seed)
torch.manual_seed(seed)

N = 1000  # 每类样本的数量
D = 2  # 每个样本的特征维度
C = 3  # 样本的类别
H = 100  # 神经网络里隐层单元的数量
X = torch.zeros(N * C, D).to(device)
Y = torch.zeros(N * C, dtype=torch.long).to(device)
for c in range(C):
    index = 0
    t = torch.linspace(0, 1, N) # 在[0，1]间均匀的取10000个数，赋给t
    # 下面的代码不用理解太多，总之是根据公式计算出三类样本（可以构成螺旋形）
    # torch.randn(N) 是得到 N 个均值为0，方差为 1 的一组随机数，注意要和 rand 区分开
    inner_var = torch.linspace( (2*math.pi/C)*c, (2*math.pi/C)*(2+c), N) + torch.randn(N) * 0.2
    
    # 每个样本的(x,y)坐标都保存在 X 里
    # Y 里存储的是样本的类别，分别为 [0, 1, 2]
    for ix in range(N * c, N * (c + 1)):
        X[ix] = t[index] * torch.FloatTensor((math.sin(inner_var[index]), math.cos(inner_var[index])))
        Y[ix] = c
        index += 1

#创建线性模型
learning_rate = 1e-3
lambda_l2 = 1e-5

# nn 包用来创建线性模型
# 每一个线性模型都包含 weight 和 bias
model = nn.Sequential(
    nn.Linear(D, H),
    nn.Linear(H, C)
)
model.to(device) # 把模型放到GPU上

# nn 包含多种不同的损失函数，这里使用的是交叉熵（cross entropy loss）损失函数
criterion = torch.nn.CrossEntropyLoss()

# 这里使用 optim 包进行随机梯度下降(stochastic gradient descent)优化
optimizer = torch.optim.SGD(model.parameters(), lr=learning_rate, weight_decay=lambda_l2)

# 开始训练
for t in range(1000):
    # 把数据输入模型，得到预测结果
    y_pred = model(X)
    # 计算损失和准确率
    loss = criterion(y_pred, Y)
    score, predicted = torch.max(y_pred, 1)
    acc = (Y == predicted).sum().float() / len(Y)
    print('[EPOCH]: %i, [LOSS]: %.6f, [ACCURACY]: %.3f' % (t, loss.item(), acc))
    display.clear_output(wait=True)

    # 反向传播前把梯度置 0 
    optimizer.zero_grad()
    # 反向传播优化 
    loss.backward()
    # 更新全部参数
    optimizer.step()

 

此图只是用了线性方法使得分类效果不是很理想

 

learning_rate = 1e-3
lambda_l2 = 1e-5

# 这里可以看到，和上面模型不同的是，在两层之间加入了一个 ReLU 激活函数
model = nn.Sequential(
    nn.Linear(D, H),
    nn.ReLU(),
    nn.Linear(H, C)
)
model.to(device)

# 下面的代码和之前是完全一样的，这里不过多叙述
criterion = torch.nn.CrossEntropyLoss()
optimizer = torch.optim.Adam(model.parameters(), lr=learning_rate, weight_decay=lambda_l2) # built-in L2

# 训练模型，和之前的代码是完全一样的
for t in range(1000):
    y_pred = model(X)
    loss = criterion(y_pred, Y)
    score, predicted = torch.max(y_pred, 1)
    acc = ((Y == predicted).sum().float() / len(Y))
    print("[EPOCH]: %i, [LOSS]: %.6f, [ACCURACY]: %.3f" % (t, loss.item(), acc))
    display.clear_output(wait=True)
    
    # zero the gradients before running the backward pass.
    optimizer.zero_grad()
    # Backward pass to compute the gradient
    loss.backward()
    # Update params
    optimizer.step()

 

 

这是加了ReLU激活函数后，使神经网络具备了分层的非线性映射学习能力。第二个图的效果明显要比上一个图要好。

 

反向传播前要清零梯度可以让梯度发挥更大的作用。

 交叉熵主要是用来判定实际的输出与期望的输出的接近程度.它主要刻画的是实际输出（概率）与期望输出（概率）的距离，也就是交叉熵的值越小，两个概率分布就越接近。

2.4 回归分析

# 这里定义了2个网络，一个 relu_model，一个 tanh_model，
# 使用了不同的激活函数
relu_model = nn.Sequential(
        nn.Linear(D, H),
        nn.ReLU(),
        nn.Linear(H, C)
)
relu_model.to(device)

tanh_model = nn.Sequential(
        nn.Linear(D, H),
        nn.Tanh(),
        nn.Linear(H, C)   
)
tanh_model.to(device)

# MSE损失函数
criterion = torch.nn.MSELoss()
# 定义优化器，使用 Adam，这里仍使用 SGD 优化器的化效果会比较差，具体原因请自行百度
optimizer_relumodel = torch.optim.Adam(relu_model.parameters(), lr=learning_rate, weight_decay=lambda_l2) 
optimizer_tanhmodel = torch.optim.Adam(tanh_model.parameters(), lr=learning_rate, weight_decay=lambda_l2) 

# 开始训练
for t in range(1000):
    y_pred_relumodel = relu_model(X)
    y_pred_tanhmodel = tanh_model(X)
    # 计算损失与准确率
    loss_relumodel = criterion(y_pred_relumodel, y)
    loss_tanhmodel = criterion(y_pred_tanhmodel, y)
    print(f"[MODEL]: relu_model, [EPOCH]: {t}, [LOSS]: {loss_relumodel.item():.6f}")
    print(f"[MODEL]: tanh_model, [EPOCH]: {t}, [LOSS]: {loss_tanhmodel.item():.6f}")    
    display.clear_output(wait=True)

    optimizer_relumodel.zero_grad()
    optimizer_tanhmodel.zero_grad()
    loss_relumodel.backward()
    loss_tanhmodel.backward()
    optimizer_relumodel.step()
    optimizer_tanhmodel.step()

plt.figure(figsize=(12, 6))

def dense_prediction(model, non_linearity):
    plt.subplot(1, 2, 1 if non_linearity == 'ReLU' else 2)
    X_new = torch.unsqueeze(torch.linspace(-1, 1, 1001), dim=1).to(device)
    with torch.no_grad():
        y_pred = model(X_new)
    plt.plot(X_new.cpu().numpy(), y_pred.cpu().numpy(), 'r-', lw=1)
    plt.scatter(X.cpu().numpy(), y.cpu().numpy(), label='data')
    plt.axis('square')
    plt.title(non_linearity + ' models')

dense_prediction(relu_model, 'ReLU')
dense_prediction(tanh_model, 'Tanh')

 

 由上图可以看到用ReLU函数处理的图像要比用Tanh函数处理的图像要好。

Adam是一种可以替代传统随机梯度下降过程的一阶优化算法，它能基于训练数据迭代地更新神经网络权重。

为什么ReLu要好过sigmoid和tanh？

第一，采用sigmoid等函数，算激活函数时（指数运算），计算量大，反向传播求误差梯度时，求导涉及除法和指数运算，计算量相对大，而采用Relu激活函数，整个过程的计算量节省很多。

第二，对于深层网络，sigmoid函数反向传播时，很容易就会出现梯度消失的情况（在sigmoid接近饱和区时，变换太缓慢，导数趋于0，这种情况会造成信息丢失），这种现象称为饱和，从而无法完成深层网络的训练，为什么会无法完成训练呢，因为神经网络更新w的时候就是依靠导数来更新的，如果导数接近0，那w更新之后还是原来的w了。而ReLU就不会有饱和倾向，不会有特别小的梯度出现。

第三，Relu会使一部分神经元的输出为0，这样就造成了网络的稀疏性，并且减少了参数的相互依存关系，缓解了过拟合问题的发生。当然现在也有一些对relu的改进，比如prelu，random relu等，在不同的数据集上会有一些训练速度上或者准确率上的改进。