【数据结构】字符串 模式匹配算法的理解与实现 Brute Force算法(BF算法)与KMP算法 （C与C++分别实现）

#笔记整理
若不了解串的定义，可至：
串（string）的定义与表示 查看

串的模式匹配算法

求子串位置的定位函数 Index(S, P, pos)
求子串的定位操作通常称作串的模式匹配（其中子串P称为模式串）。

算法1：朴素模式匹配算法/简单匹配算法（Brute-Force算法，简称BF算法）

从目标主串$s=“s_1{s}_2\dots s_n”$的第一个字符开始和模式串$p=“p_1{p}_2\dots p_m”$中的第一个字符比较,若相等,则继续逐个比较后续字符；否则从目标主串s的第二个字符开始重新与模式串p的第一个字符进行比较。依次类推,若从目标串s的第i个字符开始,每个字符依次和模式串p中的对应字符相等,则匹配成功,该算法返回i；否则,匹配失败,函数返回0。

实现代码：

// ——————————串的定长顺序存储表示————————————————
#define MAXSTRLEN 255     //最大串长
typedef char SString[MAXSTRLEN+1];

// C语言实现
int index(SString s, SString t, int pos){
    // t非空， 1 <= pos <= strlen(s)
    int i = pos;
    int j = 0;
    int sLen = strlen(s);
    int tLen = strlen(t);
    while(i < sLen && j < tLen){
        if(s[i] == t[j]){
            i++;
            j++;
        }else{
            i = i - j + 2;
            j = 1;
        }
    }
    if(j >= tLen){
        return i - tLen;
    }else{
        return 0;
    }
}

// C++实现
int index2(string s, string t, int pos){
    // t非空， 1 <= pos <= Strlength(s)
    int i = pos;
    int j = 0;
    int sLen = s.length();
    int tLen = t.length();
    while(i < sLen && j < tLen){ // s[0]、t[0]为串长度
        if(s[i] == t[j]){
            i++;
            j++;
        }else{
            i = i - j + 2;
            j = 1;
        }
    }
    if(j >= tLen){
        return i - tLen;
    }else{
        return 0;
    }
}

源代码：github地址（其中有详细注释）

朴素模式匹配算法的时间复杂度分析
主串长n； 子串长m。可能匹配成功的位置(1 ~ n-m+1)。

• 最好的情况下，
  第i个位置匹配成功，比较了（i - 1 + m）次，平均比较次数：
  最好情况下算法的平均时间复杂度O(n+m)。
• 最坏的情况下，
  第i个位置匹配成功，比较了（i * m）次，平均比较次数：
  设 n >> m，最坏情况下的平均时间复杂度为O(n * m)。

算法2：朴素模式匹配算法的改进算法：KMP算法

KMP算法是 D.E.Knuth、J.H.Morris 和 V.R.Pratt 共同提出的，简称KMP算法。该算法较BF算法有较大改进，主要是消除了主串指针的回溯，从而使算法效率有了某种程度的提高。
当主串的第 i 个字符与子串的第 j 个字符失配时，若主串的第 i 个字符前的 ( k - 1 ) 个字符与子串的前 ( k -1 ) 个字符匹配，则只需主串的第 i 个字符与子串的第 k 个字符开始向后比较即可，i 不必回溯。

为此,定义 next[] 数组，表明当模式中第 j 个字符与主串中相应字符“失配”时，在模式串中需重新和主串中该字符进行比较的字符的位置 k，即$next[j]=k$。
实现代码：

 // KMP，C语言实现
int indexKMP(SString s, SString t, int pos){
    int i = pos;
    int j = 0;
    int sLen = strlen(s);
    int tLen = strlen(t);
    int next[tLen] = {0};
    getNext(next, t, pos); // 求next数组
    //getNextImprov(next, t, pos); // 使用改进的算法求next数组，根据需要选择
    for(int x=0; x<tLen; x++){
        cout << next[x] << endl;
    }
    while(i < sLen && j < tLen){
        if(j < 0 || s[i] == t[j]){ // 若匹配，或t已移出最左侧
            i++;
            j++;
        }else{
            j = next[j]; // 和BF算法的区别在此
        }
    }
    if(j >= tLen){
        return i - tLen;
    }else{
        return 0;
    }
}

next[]数组的生成与主串无关，只和模式子串自身有关。

以下为next函数的定义与求法（注意：此处的主串和模式子串都是从下标0开始的，与书上的不一样）

求next[]数组算法步骤：

1. 初始$next[0]=-1$ 表明主串从下一字符$s_{i+1}$起和模式串重新开始匹配。因此$i=i+1;j=0;$
2. 设$next[j]=k$，求$next[j+1]$ ：
   　● 若 $p_k=p_j$ ,即$p[j]=p[next[j]]$，则有$“p_1\dots p_{k-1}{p}_k”=“p_{j-k+1}\dots p_{j-1}{p}_j”$ ，且不存在$k^{\prime }>k$满足该等式，因此$next[j+1]=k+1=next[j]+1$。
   　● 若 $p_k̸=p_j$，则令 $p[j]$ 和 $p[next[next[j]]]$ 比较；
   　　　○ 若相等，则 $next[j+1]=next[next[j]]+1$；
   　　　○若不等，则沿失败链继续查找，直到某个 $p[next[...next[j]...]]==p[j]$，或 $next[...next[j]...]==-1$，这时都置 $next[j+1]=next[...next[j]...]+1$。

实现代码：

// 生成next数组，C语言实现
void getNext(int next[], SString t, int pos){
    int i = pos;
    int j = -1;
    int tLen = strlen(t);
    next[0] = -1;
    while( i < tLen-1){
        if( j < 0 || t[i] == t[j]){ // 初始或匹配
            i++;
            j++;
            next[i] = j;
        }else{
            j = next[j];
        }
    }
}

改进 求 next[] 数组算法步骤的思路：
上述求 next 数组的步骤在模式串中相同的子串较多的情况下存在着缺陷。
如主串 ${}^{\prime }aaabaaaa{b}^{\prime }$ 在和模式子串 ${}^{\prime }aaaa{b}^{\prime }$ 匹配时，当 $i=3、j=3$ 时，${}^{\prime }{a}^{\prime }!{=}^{\prime }{b}^{\prime }$，如下图，由 KMP 算法可知，由 $next[j]$ 的指示，接下来还会进行 $i=3、j=2，i=3、j=1，i=3，j=0$ 这3次比较。实际上，因为模式中第0、1、2个字符和第3个字符都相等，因此不需要再和主串中第3个字符相比较，可以将模式一气向右移动4个字符的位置直接进行 $i=4、j=0$ 时的字符比较。
也就是说，在之前求next方法的基础上，需要再加上一个判断：
$p[j]?=p[k]$，若相等，则 $next[j]=next[k]$，否则，$next[j]=k$。

再举两个生成next数组的例子：

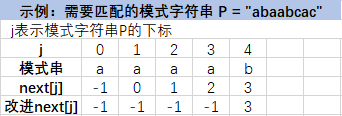
下面的例子包含了求next[j]的过程，理解该过程时暂不需要看"改进next[j]"那一行。

改进next[j]方法的计算过程由你们自己理解和验算吧。
实现代码：

// 生成next数组的改进算法，若模式串中相同的子串较多，可以使用此方法，可提高匹配效率。C语言实现
void getNextImprov(int next[], SString t, int pos ){
    int i = pos;
    int j = -1;
    int tLen = strlen(t);
    next[0] = -1;
    while( i < tLen-1){
        if( j < 0 || t[i] == t[j]){ // 初始或匹配
            i++;
            j++;
            if(t[i] != t[j]){  //改进之处
                next[i] = j;
            }else{
                next[i] = next[j];
            }
        }else{
            j = next[j];
        }
    }
}

KMP算法的时间复杂度

设主串s的长度为n,模式串t长度为m,在KMP算法中求next数组的时间复杂度为O(m),在后面的匹配中因主串s的下标不减即不回溯,比较次数可记为n,所以KMP算法总的时间复杂度为O(n+m)。

由于篇幅的关系，c++实现的代码请参考：
源代码：github地址（其中有详细注释）

部分内容来源：

1. 《数据结构（C语言版）》----严蔚敏
2. 《数据结构》课堂教学ppt ---- 刘立芳
3. 《数据结构算法与解析（STL版）》 ---- 高一凡