模式串匹配的BF算法和KMP算法
KMP是三位大牛:D.E.Knuth、J.H.Morris和V.R.Pratt同时发现的。为了解决模式匹配问题,也即寻找模式串(子串)在主串中第一次出现的位置,若模式串在主串中不存在则返回-1。
简单的模式匹配算法(BF算法)
对于简单的模式匹配,也即暴力破解,我们的想法是:从左到右一个个匹配,如果这个过程中有某个字符不匹配,就跳回去,将模式串向右移动一位。
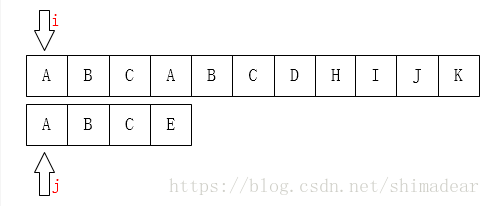
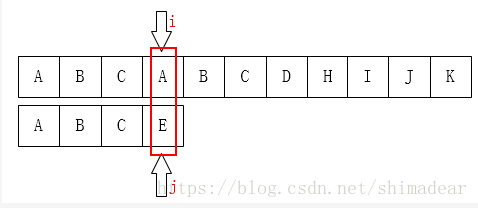
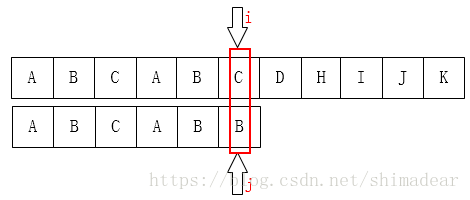
两个变量i和j分别记录主串和模式串的下标,我们只需要从左到右比较i指针指向的字符和j指针指向的字符是否一致。如果一致就都向后移动,如果不一致,如下图:
A和E不相等,那就把i指针移回第1位(假设下标从0开始),j移动到模式串的第0位,然后又重新开始这个步骤:
对此我们可以写出简单模式匹配的函数:
int BF(const char *str,const char *sub)
{
int lenstr=strlen(str);
int lensub=strlen(sub);
int i=0,j=0; //i记录主串下标,j记录模式串下标。
int k=i;
while(i算法说明:我们假设主串长度为m,模式串长度为n,则简单模式匹配算法的时间复杂度是O(n*m)。
KMP算法
而KMP算法可以充分利用模式串的部分匹配信息,保持主串i指针不变(不需要回溯主串),通过修改模式串j指针(变动的是模式串下标),让模式串尽量移动到有效的位置,以减少比较次数。可以实现算法时间复杂度为O(m+n)。
这里我们引入一个数组next[]。
定义:next[j]为模式串位置与主串位置i失配时,滑动模式串使其模式串位置为next[j]的字符与主串位置i的字符继续匹配。
那么当模式串中某一个字符与主串不匹配时,j指针要移动到哪?
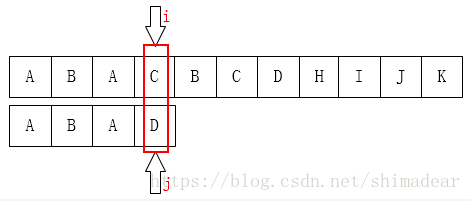
如上图:
C和D不匹配了,我们要把j移动到哪?显然是下标为1位。为什么?因为前面有一个A相同啊。
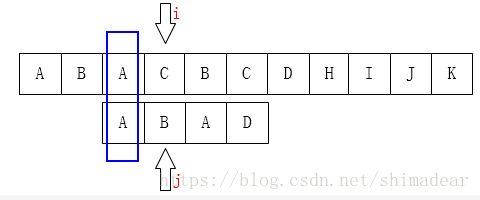
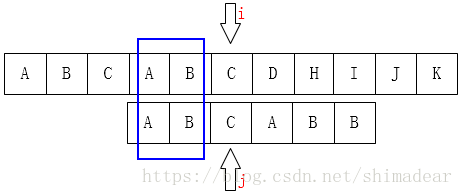
如下图也是同样情况:
可以把j指针移动到下标为2位置,因为前面有两个字母是一样的:
至此我们可以大概看出一点端倪,当匹配失败时,j要移动的下一个位置k。存在着这样的性质:最前面的k个字符和j之前的最后k个字符是一样的。
next[j]的含义就是一个固定字符串(下标从0到j-1)的最长前缀和最长后缀相同的长度。
规定特殊情况next[0]=-1。
比如:abcjkdabc,那么这个数组的最长前缀和最长后缀相同必然是3(abc)。
cbcbc,最长前缀和最长后缀相同是3(cbc)。
abcbc,最长前缀和最长后缀相同是不存在的为0。
注意最长前缀:是说以第一个字符开始,但是不包含最后一个字符。
比如aaaa相同的最长前缀和最长后缀是3(aaa)。
给定一个模式串,我们可以计算数组next[],在进行模式串匹配过程中哪里失配直接查找next[]数组对应的值即可。
如:
下标号 0 1 2 3 4 5 6 7 8 9
模式串 a b a b a b a b a a
next[]值 -1 0 0 1 2 3 4 5 6 7
现在我们需要写出计算next[]的函数了。
这里我们借鉴数学归纳法的三个步骤(或者说是动态规划?):
1、初始状态
2、假设第j位以及第j位之前的我们都填完了
3、推论第j+1位该怎么填
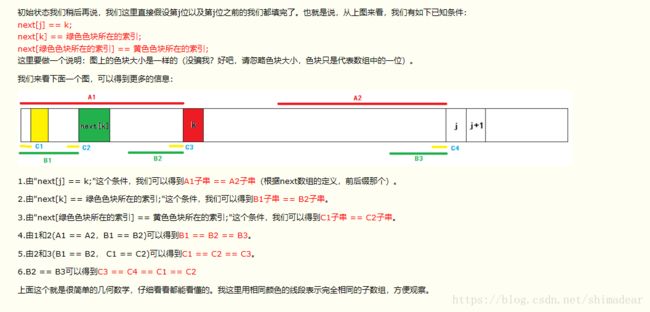
接下来,我们开始用上面得到的条件来推导如果第j+1位失配时,我们应该填写next[j+1]为多少?
next[j+1]即是找模式串中从0到j这个子串的最大前后缀:
#:(#:在这里是个标记,后面会用)我们已知A1 == A2,那么A1和A2分别往后增加一个字符后是否还相等呢?我们得分情况讨论:
(1)如果str[k] == str[j],很明显,我们的next[j+1]就直接等于k+1。
用代码来写就是next[++j] = ++k;
(2)如果str[k] != str[j],那么我们只能从已知的,除了A1,A2之外,最长的B1,B3这个前后缀来做文章了。
那么B1和B3分别往后增加一个字符后是否还相等呢?
由于next[k] == 绿色色块所在的索引,我们先让k = next[k],把k挪到绿色色块的位置,这样我们就可以递归调用"#:"标记处的逻辑了。
由于j+1位之前的next数组我们都是假设已经求出来了的,因此,上面这个递归总会结束,从而得到next[j+1]的值。
另外有个特殊情况是k为-1时,不能继续递归了,此时next[j+1]应该等于0,即把j回退到首位。
即 next[j+1] = 0; 也可以写成next[++j] = ++k;
接下来,只欠初始条件了:
next[0] = -1, next[1]=0
k = 0, j = 1
至此,可以写出求next[]数组的函数:
void GetNext(const char *sub,int *next)
{
int lensub=strlen(sub);
/*初始条件*/
next[0]=-1;
next[1]=0;
int j=1;
int k=0;
/*根据已知的前j位推测第j+1位*/
while((j+1)KMP函数:
int KMP(const char *str,const char *sub)
{
int lenstr=strlen(str);
int lensub=strlen(sub);
int i=0,j=0;
int *next=(int *)malloc(lensub*sizeof(int));
GetNext(sub,next);
while(i测试代码:
int main()
{
char str[]="ababacdabcdababc";
char sub[]="ababc";
int n=KMP(str,sub);
printf("%d\n",n);
return 0;
}