数论基础的补充讲解
数论基础的补充讲解
整除的一些性质:
(1)能被2整除的数,个位上的数都能被2整除
(2*)能被4整除的数,个位和十位所组成的两位数能被4整除
(3*)能被8整除的数,百位、十位和个位所组成的三位数能被8整除
(4)能被5整除的数,末尾是0或5
(5*)能被25整除的数,十位和个位所组成的两位数能被25整除
(6*)能被125整除的数,百位、十位和个位所组成的三位数能被125整除
(7)能被3整除的数,各个数位上的数字之和能被3整除
(8*)能被9整除的数,各个数位上的数字和能被 9 整除
(9)如果一个数既能被 2 整除又能被 3 整除,那么这个数能被 6 整除
(10)如果一个数既能被 2 整除又能被 5 整除,那么这个数能被 10 整除(即个位为0)
(11*)能被 11 整除的数,奇数位(从左往右数)上的数字和与偶数位上的数字和的差(大数减小数)能被 11 整除
小数的GCD:
eps控制精度,fmod是C++的库函数,运算浮点数的mod运算。
拓展欧几里得:
Ps:关于欧几里得和拓展欧几里得可以参考我的另外一篇博文《欧几里得 & 拓展欧几里得算法 讲解 (Euclid & Extend- Euclid Algorithm)》
(1)求解不定方程:
所谓不定方程,即未知数的个数多于方程个数,且未知数受到某些限制(如要求是有理数、整数或正整数等等)的方程或方程组。
如3x-4y==6,方程只有一个,但是解却可以有多个。
求解不定方程的一组解,或者判断不定方程是否有解,扩展欧几里得就可以派上用场了。
(2)求解模线性方程(线性同余方程):
求解ax≡b(mod p),未知数x的最小解。
(3)求解模的逆元:
同余方程ax≡b(mod n),如果gcd(a,n)==1,则方程只有唯一解。在这种情况下,如果b==1,同余方程就是ax ≡ 1(mod n),gcd(a,n)=1。这时称求出的x为a的对模n乘法的逆元。
PS:关于逆元,有一个蛮有用的性质:
设p为素数,(a/b)% p = a * b^(p-2) % p ,这样就可以将除法处理为乘法。
素数:
定义
素数是大于1的正整数,并且除了1和其本身不能被其他的正整数整除。
非素数称为合数。
素数的 eratosthenes 筛法
筛法是数论中一个比较重要的算法,在O(sqrt(N))的时间内获得N以内所有的素数。
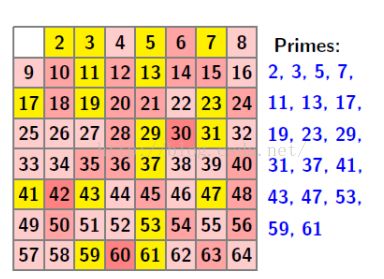
所谓筛法,就是每次筛去一部分数。如图,起始所有的数都标记为素数,遇到2时,将所有2的倍数标记为合数,以此类推下去,剩下的都是素数了。
该算法适用于较小的MAXN,对于较大的MAXN,内存无法开如此大的空间。
区间素数
获得[L , U]区间的素数,L和U很大,但是U-L不是很大。
首先线性筛出1到sqrt(2147483647)之间所有的素数(2147483647是啥?自个儿猜去~),然后再通过已经晒好素数筛出给定区间的素数。
算是模板吧,此处不贴代码~
素数判定
试除法
就是大家都会的简单算法,用小于该数的所有素数去试除,若都无法整除,则为素数,复杂度O(sqrt(N)).
Miller-Robin随机素性测试
关于Miller-Robin算法,可以另劈一章进行讲解,因而此处只做简略介绍。
Miller-Rober 带有随机性,可能测出伪素数,概率为1/(2^s),一般 s 为 20 左右,
因而失误概率很低,适用于大数素性判断。
关于Miller-Robin的时间复杂度,最坏为(1+O(1))*log2(N)。Miller- Rabin算法的性能是很好的。在实际应用中,Miller-Rabin的实际执行速度也很快。
唯一分解理论
定义:自然数N皆可以表示为素数之积
一些结论:
①、N的约数个数,为(x1+1)*(x2+1)*……*(xm+1)
分解质因子
普通的分解质因数
对n进行分解质因子,将分解的因子存入数组facs中,长度为cnt。
先找一个最小的质数k;
若该质数等于n,则分解质因子的过程已经结束;
若n>k,且k|n,则记录k,n/=k,然后继续寻找;
若n不能被k整除,k+=2,继续寻找。
Pollard_rho因数分解
适用于大数的分解质因子,返回的质因子无序。
欧拉函数
中国剩余定理
参考资料:
①、东北师范大学数论基础讲解