机器学习：SVC实战+源码解读（支持向量机用于分类）

这部分只是对支持向量机sklearn库函数调用，参数解释，以及各个参数对测试结果的影响分析。个人认为入门机器学习实战的最快实例。

一.线性分类SVM

调用sklearn包中的LinearSVC

下面是调用的初始值：

 def __init__(self, penalty='l2', loss='squared_hinge', dual=True, tol=1e-4,
                 C=1.0, multi_class='ovr', fit_intercept=True,
                 intercept_scaling=1, class_weight=None, verbose=0,
                 random_state=None, max_iter=1000)

其中参数如下：

C：一个浮点数，惩罚参数

Loss:字符串，表示损失函数，

         ‘hinge’：合页损失，标准SVM的损失函数；

         ‘squared_hinge’:合页损失的平方。

penalty：指定‘l1’或者'l2'，惩罚项的范数，默认为‘l2’

dual： 布尔值，如果为true，则解决对偶问题；如果是false，则解决原始问题。当样本数大于特征数，倾向于false;

tol：指定终止迭代的阈值。

multi_class：指定多分类策略，

                   ‘ovr’：采用one-vs-rest分类策略；默认

                  'crammer_singer'：多类联合分类，很少用

fit_intercept:布尔值，如果为true，则计算截距，即决策函数中的常数项，否则，忽略截距。

class_weight：可以是一个字典，指定各个类的权重，若未提供，则认为类的权重为1；

其属性如下：

coef_:返回各个特征的权重。

intercept_:一个数组，决策函数的常数项

方法：

fit(x,y)：训练模型

predict(x):用模型进行预测，返回预测值；

score(x,y)：返回预测准确率

1.简单的线性可分支持向量机

from  sklearn  import svm, datasets,cross_validation
#加载鸢尾花数据集
def load_data_classfication():
    iris=datasets.load_iris()
    X_train=iris.data
    y_train=iris.target
    return cross_validation.train_test_split(X_train,y_train,test_size=0.25,random_state=0,stratify=y_train)

#使用svc分类器对其分类
def test_LinearSVC(*data):
    X_train,X_test,y_train,y_test=data
    cls=svm.LinearSVC()
    cls.fit(X_train,y_train)
    print('Score:%.2f'% cls.score(X_test,y_test))
    print('Coefficients:%s,intercept:%s'%(cls.coef_,cls.intercept_))

X_train,X_test,y_train,y_test=load_data_classfication()
test_LinearSVC(X_train,X_test,y_train,y_test)

将鸢尾花数据分类三类，其中每一个样本都有四个特征，花萼的长宽，花瓣的长宽

Score:0.97
Coefficients:[[ 0.20959539  0.3992385  -0.81739225 -0.44231995]
 [-0.12568317 -0.78049158  0.51754286 -1.0251776 ]
 [-0.80282255 -0.87632578  1.21360546  1.80985929]],intercept:[ 0.1197369   2.02403826 -1.4441551 ]

上面是检测结果，以及每个特征对于分类的影响

2.考察损失函数对于分类结果的影响

def test_LinearSVC_loss(*data):
    X_train, X_test, y_train, y_test = data
    losses=['hinge','squared_hinge']
    for loss in losses:
        cls=svm.LinearSVC(loss=loss)
        cls.fit(X_train,y_train)
        print("loss:%s"%loss)
        print('Coefficients:%s,intercept %s'%(cls.coef_,cls.intercept_))
        print('Score:%.2f' % cls.score(X_test, y_test))
X_train,X_test,y_train,y_test=load_data_classfication()
test_LinearSVC_loss(X_train,X_test,y_train,y_test)

结果：

loss:hinge
Coefficients:[[ 0.36636819  0.32163591 -1.07533939 -0.57004684]
 [ 0.46789769 -1.55869702  0.39897097 -1.34402625]
 [-1.21507089 -1.15278116  1.84779924  1.98442388]],intercept [ 0.18050217  1.36129524 -1.42624543]
Score:0.97
loss:squared_hinge
Coefficients:[[ 0.20959889  0.39924259 -0.8173887  -0.44231943]
 [-0.12966115 -0.78597293  0.52178887 -1.02424942]
 [-0.80322699 -0.87607737  1.21376071  1.81009443]],intercept [ 0.11973969  2.04293055 -1.44409524]
Score:0.97

3.惩罚项的系数对结果的影响，C衡量了误分类点的重要性，C越大则错误分类点越重要

def test_LinearSVC_C(*data):
    X_train, X_test, y_train, y_test = data
    Cs=np.logspace(-2,1)
    train_score=[]
    test_score=[]
    for C in Cs:
        cls=svm.LinearSVC(C=C)
        cls.fit(X_train,y_train)
        train_score.append(cls.score(X_train,y_train))
        test_score.append(cls.score(X_test,y_test))
    fig=plt.figure()
    ax=fig.add_subplot(1,1,1)
    ax.plot(Cs,train_score,label="Traing score")
    ax.plot(Cs,test_score,label="test score")
    ax.set_xlabel(r"C")
    ax.set_ylabel(r"score")
    ax.set_xscale('log')
    ax.set_title("LinearSVC")
    ax.legend(loc='best')
    plt.show()
X_train,X_test,y_train,y_test=load_data_classfication()
test_LinearSVC_C(X_train,X_test,y_train,y_test)

可以看出，C越小，错误分类点重要性低，误分类点较多，分类器性能较差。

 二、非线性分类器

from sklearn import svm
svm.SVC()
#下面是初始化参数  
def __init__(self, C=1.0, kernel='rbf', degree=3, gamma='auto',
                 coef0=0.0, shrinking=True, probability=False,
                 tol=1e-3, cache_size=200, class_weight=None,
                 verbose=False, max_iter=-1, decision_function_shape='ovr',
                 random_state=None):

非线性分类器就是引入了核函数，将在原始空间中的特征映射到更高维度，用于分类

参数解释：

keral：指定核函数

             'linear':线性核函数

          'poly'：多项式核函数

             'rbf'：高斯核函数

               'sigmoid'：S核函数

属性解释：

support_:一个数组，支持向量下标

support_vectors_:一个数组，支持向量

方法：

predict_log_proba(x):返回一个数组，数组元素依次是预测为各个类别的概率的对数值。

predict_proba(x):返回一个数组，数组的元素依次是预测为各个类别的概率值

1.查看多项式中的参数如何影响测试结果

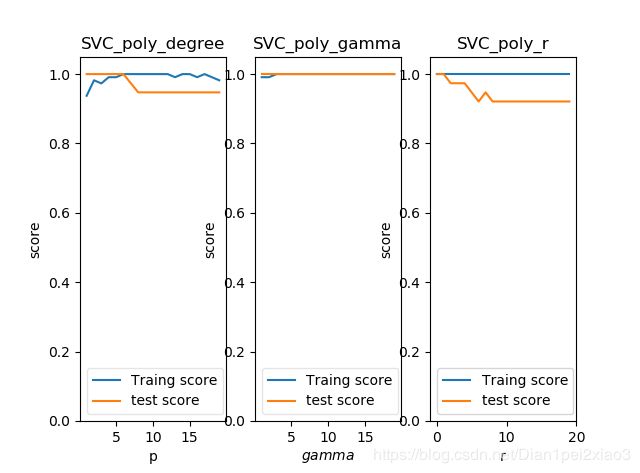
def test_SVC_poly(*data):
    X_train, X_test, y_train, y_test = data
    fig=plt.figure()
    degrees=range(1,20)
    train_score = []
    test_score = []
    for degree in degrees:
        cls = svm.SVC(kernel='poly',degree=degree)
        cls.fit(X_train, y_train)
        train_score.append(cls.score(X_train, y_train))
        test_score.append(cls.score(X_test, y_test))
    ax = fig.add_subplot(1, 3, 1)
    ax.plot(degrees, train_score, label="Traing score")
    ax.plot(degrees, test_score, label="test score")
    ax.set_xlabel("p")
    ax.set_ylabel("score")
    ax.set_ylim(0,1.05)
    ax.set_title("SVC_poly_degree")
    ax.legend(loc='best',framealpha=0.5)
    ##测试gamma
    gammas=range(1,20)
    train_score = []
    test_score = []
    for gamma in gammas:
        cls = svm.SVC(kernel='poly', gamma=gamma,degree=3)
        cls.fit(X_train, y_train)
        train_score.append(cls.score(X_train, y_train))
        test_score.append(cls.score(X_test, y_test))
    ax = fig.add_subplot(1, 3, 2)
    ax.plot(degrees, train_score, label="Traing score")
    ax.plot(degrees, test_score, label="test score")
    ax.set_xlabel(r"$gamma$")
    ax.set_ylabel("score")
    ax.set_ylim(0, 1.05)
    ax.set_title("SVC_poly_gamma")
    ax.legend(loc='best', framealpha=0.5)

    ###测试R
    rs=range(0,20)
    train_score = []
    test_score = []
    for r in rs:
        cls = svm.SVC(kernel='poly',gamma=10,degree=3,coef0=r)
        cls.fit(X_train, y_train)
        train_score.append(cls.score(X_train, y_train))
        test_score.append(cls.score(X_test, y_test))
    ax = fig.add_subplot(1, 3, 3)
    ax.plot(rs, train_score, label="Traing score")
    ax.plot(rs, test_score, label="test score")
    ax.set_xlabel(r"r")
    ax.set_ylabel("score")
    ax.set_ylim(0, 1.05)
    ax.set_title("SVC_poly_r")
    ax.legend(loc='best')
    plt.show()

X_train,X_test,y_train,y_test=load_data_classfication()
test_SVC_poly(X_train,X_test,y_train,y_test)

2.高斯核函数的影响

def test_SVC_rbf(*data):
    X_train, X_test, y_train, y_test = data

    gammas = range(1, 20)
    train_score = []
    test_score = []
    for gamma in gammas:
        cls = svm.SVC(kernel='rbf', gamma=gamma)
        cls.fit(X_train, y_train)
        train_score.append(cls.score(X_train, y_train))
        test_score.append(cls.score(X_test, y_test))
    fig=plt.figure()
    ax = fig.add_subplot(1, 1, 1)
    ax.plot(gammas, train_score, label="Traing score")
    ax.plot(gammas, test_score, label="test score")
    ax.set_xlabel(r"$gammas$")
    ax.set_ylabel("score")
    ax.set_ylim(0, 1.05)
    ax.set_title("SVC_rbf")
    ax.legend(loc='best', framealpha=0.5)
    plt.show()
X_train,X_test,y_train,y_test=load_data_classfication()
test_SVC_rbf(X_train,X_test,y_train,y_test)

预测性能随gammas变化比较平稳。

参考书籍：

《Python大战机器学习》