浅谈Tarjan算法求LCA

Tarjan是一个很厉害的人，不少算法（包括一些数据结构比如splay）都是他发明的…

---

Tarjan求LCA是利用并查集的思想进行操作的

首先我们有如下的思路

void Tarjan(int u){
    fa[u]=u;
    for(register int i=head[u];i;i=line[i].nxt){
        int v=line[i].to;
        if(v!=father[u]){
            Tarjan(v);
            fa[v]=u;
        }
    }
    for(register int i=head_question[u];i;i=question[i].nxt){
        int v=question[i].to;
        if(!fa[v]) question[i].lca=find(v);
    }
}

如果没有学过Tarjan求LCA的朋友看这里可能会有一些看不懂，现在我来解释一下其中的变量和数组的含义已经算法的大概思路

---

数据结构讲解：

首先 fa 数组表示的并查集中的那个 fa ，而 father 数组是在先前的 dfs 遍历的时候处理出来了的树上的 father ， head 数组和 line 数组存的是树形结构的边（这里是邻接表结构），而 headquestion 和 question 存的是问题的那条链的首尾处（也就是询问的那两个点的 LCA ）， question[i].lca 存的是该询问的 lca ，那么显然这两个数据结构应该是这样的

struct Line{
    int val,from,to,nxt;
};

以及

struct question{
    int from,to,lca,nxt;
};

显然这是一个离线算法，也就是说，我需要把所有的处理先离线到结构体中

---

算法讲解：

现在了解了数据结构之后我们来看看算法的内容以及实现，每次访问到一个数，我们就把其并查集中的fa设置为自己，这与普通并查集的操作是一样的，然后进行向下的访问，只要不往回访问，则往下继续递归操作，回来的时候把v的fa重置为u，也是并查集的操作，表示v可以追溯到u。
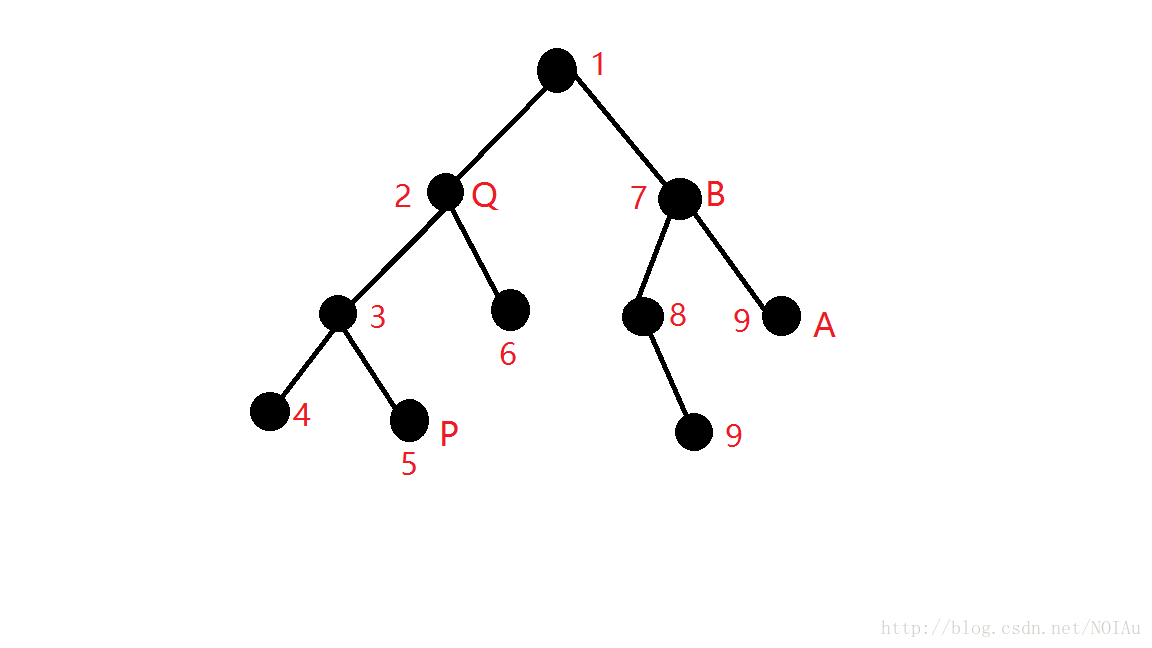
对于u的所有子点及子点的子孙已经访问完了之后，我们枚举所有和u有关的询问，试想一张图

假设我们的询问是

P-Q，P-B，A-Q

其中点上的数字是我们访问的 dfs 序，显然我们在处理 Q 的时候会递归处理到所有的 Q 的子孙，那么如果是在 Q 的 dfs 树中处理到的点，我们发现无论如何其子点和 Q 点的 fa 都不可能高过 Q 点，因为我们进这一层 dfs 树的时候， Q 点的 fa 数组置成了 Q 点本身，所以我们在访问其子点 P 点的时候，会发现 Q 点已经被访问过了，而 P 点是 Q 的子树中的点，所以他们的 LCA 就是当前 Q 所能追溯到的最早的 fa ，从 P 点往上走，到 Q 点的时候，枚举所有和 Q 有关系的询问，发现可以找到 P 点和 A 点，对于 P 点，寻找 P 点和 Q 点的 LCA ，就要找 P 点的最早能追溯到的祖先
我们发现 P 点网上追溯的时候，最多只能追溯到 Q 点，因为 Q 点的 fa 还是自己本身没有变，所有没有影响，对于 A 点，我们发现 A 点还没有处理过，也就是说 fa[A]==0， 这个时候 A 并没有在这个 dfs 树中，也没有在并查集这个数据结构中，所以我们并不能对其进行处理，继续往上走，然后往 7 号节点访问，访问 B ，然后访问 B 的所有子点，回来的时候，枚举和 B 有关的所有询问，发现和 P 点有连接，而 P 点可以追溯到的最早的祖先是 1 号节点，因为在 3 号节点访问 P 节点的时候，将 P 节点的 fa 赋成了 3 号节点，而 3 号节点及其子树访问完的时候 3 号节点的 fa 又变成了 2 号节点， 2 号节点及其子树访问完了之后， 2 号节点的 fa 又赋值成 1 号节点，所以利用并查集的性质，我们可以追溯到的最先的祖先应该是 1 号节点
而我们当前的 dfs 树也是最高只能访问到 1 号节点，所以是从 1 号节点往右访问，访问到的 B 节点，所以他们的 LCA 就应该是 1 号节点，讲到这里， Tarjan 算法求 LCA 的大致过程就已经讲完了，那么 Tarjan 求 LCA 的完整版代码应该包括第一遍的 dfs 求 dfs 序和 father 以及并查集的 find 函数

---

完整代码实现：

void dfs(int u,int fat,int cnt){
    father[u]=fat;
    dfn[u]=++timer;
    deep[u]=cnt;
    for(register int i=head[u];i;i=line[i].nxt){
        int v=line[i].to;
        if(v!=fat) dfs(v,u,cnt+line[i].val);
    }
}
int find(int x){
    return x=fa[x]?x:fa[x]=find(x);
} 
void Tarjan(int u){
    fa[u]=u;
    for(register int i=head[u];i;i=line[i].nxt){
        int v=line[i].to;
        if(v!=father[u]){
            Tarjan(v);
            fa[v]=u;
        }
    }
    for(register int i=head_question[u];i;i=question[i].nxt){
        int v=question[i].to;
        if(!fa[v]) question[i].lca=find(v);
    }
}

值得注意的是，第一个dfs函数中还可以顺便处理一些其他数据，比如说对于一些边有权值的题目，还可以顺便处理一个深度，也就是上述代码中的deep数组所存储的数据