位置编码
绝对位置
vanilla Transformer中的绝对位置编码,
$$\begin{equation}PE(pos,2i)=\sin(pos/10000^{\frac{2i}{d_{model}}})\tag{1}\end{equation}$$
$$\begin{equation}PE(pos,2i+1)=\cos(pos/10000^{\frac{2i}{d_{model}}})\tag{2}\end{equation}$$
def positional_embedding(pos_seq, inv_freq, bsz=None):
sinusoid_inp = tf.einsum('i,j->ij', pos_seq, inv_freq)
pos_emb = tf.concat([tf.sin(sinusoid_inp), tf.cos(sinusoid_inp)], -1)
if bsz is not None:
return tf.tile(pos_emb[:, None, :], [1, bsz, 1])
else:
return pos_emb[:, None, :]pos_seq和inv_freq分别为
pos_seq = tf.range(klen - 1, -1, -1.0)
inv_freq = 1 / (10000 ** (tf.range(0, d_model, 2.0) / d_model)) position embeding的实现略有些不同,sinusoid_inp的shape为[len_pos, d_model//2],len_pos为序列长度,d_model为embedding的维度。因此,实际得到的postition embedding,前d_model//2维采用的是式(1),后d_model//2维采用的是式(2)。
相对位置
$$\begin{equation}h_{t+1}=f(h_t,E_{s_{t+1}}+U_{1:L})\tag{3}\end{equation}$$
$t+1$时刻的segment的hidden state,依赖于前一时刻segment的hidden state $h_t$,以及当前时刻输入序列$s_{t+1}$的word embedding $E_{s_{t+1}}$和绝对位置编码$U_{1:L}$。显然,这样存在一个问题,即位置编码$U_{1:L}$对所有的segment都是一样的,对于输入$x_{t,j}$和$x_{t+1,j}$($j=1,\cdots,L$),模型无法区别两者的位置embedding。
为了解决这一问题,transformer-xl采用相对位置编码。
在vanilla Transformer中,scaled dot-product attention的计算方式为
$$\begin{equation}Attention(Q,K,V)=softmax(\frac{QK^T}{\sqrt{d_k}})V\tag{4}\end{equation}$$
使用绝度位置编码,计算query $q_i$和key $k_j$之间的attention score,
$$\begin{equation}\begin{aligned}A_{i,j}^{abs}&=(E^T_{x_i}+U^T_i)W^T_q((E^T_{x_j}+U^T_j)W_k^T)^T\\&=(E^T_{x_i}+U^T_i)W^T_qW_k(E_{x_j}+U_j)\\&=\underbrace{E^T_{x_i}W^T_qW_kE_{x_j}}_{(a)}+\underbrace{E^T_{x_i}W^T_qW_kU_j}_{(b)}\\&+\underbrace{U^T_iW^T_qW_kE_{x_j}}_{(c)}+\underbrace{U^T_iW^T_qW_kU_j}_{(d)}\end{aligned}\tag{5}\end{equation}$$
其中,$U_i$和$U_j$为绝对位置编码。对式(xx)进行改进,引入相对位置编码,
$$\begin{equation}\begin{aligned}A_{i,j}^{rel}&=\underbrace{E^T_{x_i}W^T_qW_{k,E}E_{x_j}}_{(a)}+\underbrace{E^T_{x_i}W^T_qW_{k,R}R_{i-j}}_{(b)}\\&+\underbrace{u^TW_{k,E}E_{x_j}}_{(c)}+\underbrace{v^TW_{k,R}R_{i-j}}_{(d)}\end{aligned}\tag{6}\end{equation}$$
主要有3点改进
- 将式(xx)中的绝对位置编码$U_j$改为相对位置编码$R_{i-j}$,因此在计算attention score关注的是相对位置$i-j$。$R$为sinusoid encoding matrix,其参数不参与训练;
- 分别使用$u\in \mathbb{R}^d$和$v\in \mathbb{R}^d$替换项$(c)$和项$(d)$中的$U_i^TW_q^T$,论文的解释是
In this case, since the query vector is the same for all query positions, it suggests that the attentive bias towards different words should remain the same regardless of the query position。即,$U_i^TW_q^T\rightarrow R_{i-i}^TW^T_q=R^T_0W_q^T$,不管query position是什么,都是一样的。$u$和$v$在训练过程中参与更新。(这里不太明白,为什么使用不一样的$u$和$v$) - 将原始的权重矩阵$W_k$变为$W_{k,E}$和$W_{k,R}$,分别用来产生基于内容的key vector和基于位置的key vector。
位置编码的trick
如式(6)所示,$A_{i,j}^{rel}$需要计算$W_{k,R}R_{i-j}$,注意到相对距离$i-j$只可能是0~M+L-1的整数,其中M为memory的长度(memory length),L为一个segment的序列长度(segment length)。
假设当前时刻segment的长度为$L$,输入为$(x_1, \cdots,x_L)$,memory的长度为M,memory 序列为$(x_{-(M-1)},\cdots,x_{-1}, x_{0})$。对于输入$x_1$,它可以使用的历史信息为$x_{-(M-1)},\cdots,x_{-1}, x_{0},x_{1}$,对于输入$x_2$,它可以使用的历史信息为$x_{-(M-1)},\cdots,x_{-1}, x_{0},x_{1},x_{2}$,对于输入$x_L$,它可以使用的历史信息为$x_{-(M-1)},\cdots,x_{-1}, x_{0},x_{1},x_{2},\cdots,x_{L}$。对于所有可能的(i,j),有$\{(i,j)|i=1,\cdots,L,j=-(M-1),\cdots,i\}$,计算式(6)的(b)项中的$W_{k,R}R_{i-j}$,得到行矩阵
$$\begin{equation}Q:=\begin{bmatrix}R_{M+L-1}^T \\ R_{M+L-2}^T \\ \vdots \\ R_1^T \\ R_0^T\end{bmatrix}W_{k,R}^T=\begin{bmatrix}[W_{k,R}R_{M+L-1}]^T \\ [W_{k,R}R_{M+L-2}]^T \\ \vdots \\ [W_{k,R}R_1]^T \\ [W_{k,R}R_0]^T\end{bmatrix}\in \mathbb{R}^{(M+L)\times d}\tag{7}\end{equation}$$
令式(6)的(b)项中的$E_{x_i}^TW_q^T=q_{i-1}^T$,则考虑所有合理(i,j),(b)项可写为矩阵的形式
$$\begin{equation}\begin{aligned}B&=\begin{bmatrix}q_0^TW_{k,R}R_M & \cdots & q_0^TW_{k,R}R_0 & 0 & \cdots & 0 \\ q_1^TW_{k,R}R_{M+1} & \cdots & q_1^TW_{k,R}R_1 & q_1^TW_{k,R}R_0 & \vdots & 0 \\ \vdots & \vdots & \vdots & \vdots & \ddots & \vdots \\ q_{L-1}^TW_{k,R}R_{M+L-1} & \cdots & q_{L-1}^TW_{k,R}R_{L} & q_{L-1}^TW_{k,R}R_{L-1} & \cdots & q_{L-1}^TW_{k,R}R_{0}\end{bmatrix}\\ &=\begin{bmatrix}q_0^TQ_{L-1} & \cdots & q_0^TQ_{M+L-1} & 0 & \cdots & 0 \\ q_1^tQ_{L-2} & \cdots & q_1^TQ_{M+L-2} & q_1^TW_{k,R}Q_{M+L-1} & \vdots & 0 \\ \vdots & \vdots & \vdots & \vdots & \ddots & \vdots \\ q_{L-1}^TQ_0 & \cdots & q_{L-1}^TQ_M & q_{L-1}^TQ_{M+1} & \cdots & q_{L-1}^TQ_{M+L-1}\end{bmatrix}\end{aligned}\tag{8}\end{equation}$$
定义$\tilde{Q}$为如下矩阵形式
$$\begin{equation}\tilde{Q}=qQ^T=\begin{bmatrix} q_{0}^TQ_0 & \cdots & q_{0}^TQ_M & q_{0}^TQ_{M+1} & \cdots & q_{0}^TQ_{M+L-1} \\ q_{1}^TQ_0 & \cdots & q_{1}^TQ_M & q_{1}^TQ_{M+1} & \cdots & q_{1}^TQ_{M+L-1} \\ \vdots & \vdots & \vdots & \vdots & \ddots & \vdots \\ q_{L-1}^TQ_0 & \cdots & q_{L-1}^TQ_M & q_{L-1}^TQ_{M+1} & \cdots & q_{L-1}^TQ_{M+L-1}\end{bmatrix}\tag{9}\end{equation}$$
可以返现,通过将矩阵$\tilde{B}$的第i行左移$L-i$位,即可得到$B$。因此,在计算式(6)的(b)项时,可以先计算$qQ^T$得到$\tilde{Q}$,再进行左移操作,得到$B$。
实现左移
def rel_shift(x):
x_size = tf.shape(x)
x = tf.pad(x, [[0, 0], [1, 0], [0, 0], [0, 0]])
x = tf.reshape(x, [x_size[1] + 1, x_size[0], x_size[2], x_size[3]])
x = tf.slice(x, [1, 0, 0, 0], [-1, -1, -1, -1])
x = tf.reshape(x, x_size)
return x这篇论文【代码解析】Transformer-XL 之 Relative Positional Encodings的图例很好。
def rel_multihead_attn(w, r, r_w_bias, r_r_bias, attn_mask, mems, d_model,
n_head, d_head, dropout, dropatt, is_training,
kernel_initializer, scope='rel_attn'):
scale = 1 / (d_head ** 0.5) # 防止内积过大?
with tf.variable_scope(scope):
qlen = tf.shape(w)[0]
rlen = tf.shape(r)[0] # =k_len
bsz = tf.shape(w)[1]
cat = tf.concat([mems, w], # [m_len, bsz, emb_dim] [q_len, bsz. emb_dim] = [k_len=m_len+q_len, bsz, emb_dim]
0) if mems is not None and mems.shape.ndims > 1 else w
# [k_len, bsz, 3*n_head*d_head]
w_heads = tf.layers.dense(cat, 3 * n_head * d_head, use_bias=False,
kernel_initializer=kernel_initializer, name='qkv')
# r_head_k: [rlen, bsz, n_head*d_head]
r_head_k = tf.layers.dense(r, n_head * d_head, use_bias=False,
kernel_initializer=kernel_initializer, name='r')
w_head_q, w_head_k, w_head_v = tf.split(w_heads, 3, -1)
w_head_q = w_head_q[-qlen:] # query只有前q_len
klen = tf.shape(w_head_k)[0]
w_head_q = tf.reshape(w_head_q, [qlen, bsz, n_head, d_head])
w_head_k = tf.reshape(w_head_k, [klen, bsz, n_head, d_head])
w_head_v = tf.reshape(w_head_v, [klen, bsz, n_head, d_head])
r_head_k = tf.reshape(r_head_k, [rlen, n_head, d_head])
rw_head_q = w_head_q + r_w_bias # E_x W_q + u [qlen, bsz, n_head, d_head]
rr_head_q = w_head_q + r_r_bias # E_x W_q + v
# AC [qlen, klen, bsz, n_head]
AC = tf.einsum('ibnd,jbnd->ijbn', rw_head_q, w_head_k) # term a + term c
# [qlen, rlen, bsz, n_head]
BD = tf.einsum('ibnd,jnd->ijbn', rr_head_q, r_head_k) # term b + term d
BD = rel_shift(BD)
attn_score = (AC + BD) * scale
attn_mask_t = attn_mask[:, :, None, None] # attention mask 保证每一个只会用到前k_len-1个
attn_score = attn_score * (1 - attn_mask_t) - 1e30 * attn_mask_t
attn_prob = tf.nn.softmax(attn_score, 1) # [qlen, klen, bsz, n_head]
attn_prob = tf.layers.dropout(attn_prob, dropatt, training=is_training)
# [qlen, klen, bsz, n_head] [klen, bsz, n_head, d_head] -> [qlen, bsz, n_head, d_head]
attn_vec = tf.einsum('ijbn,jbnd->ibnd', attn_prob, w_head_v)
size_t = tf.shape(attn_vec)
# 多头拼接
attn_vec = tf.reshape(attn_vec, [size_t[0], size_t[1], n_head * d_head])
# 使维度等于输入维度,方便加残差
attn_out = tf.layers.dense(attn_vec, d_model, use_bias=False,
kernel_initializer=kernel_initializer, name='o')
attn_out = tf.layers.dropout(attn_out, dropout, training=is_training)
output = tf.contrib.layers.layer_norm(attn_out + w, begin_norm_axis=-1)
return output为了保证在计算$t+1$时刻的segment的第$j$个位置($j=1,\cdots,q\_len$)的hidden state时,不使用位置$j$之后的信息,需要对attention score进行mask操作。attn_score = (AC + BD) * scale attn_mask_t = attn_mask[:, :, None, None] # attention mask attn_score = attn_score * (1 - attn_mask_t) - 1e30 * attn_mask_t
其中attn_mask的计算方式如下,
def _create_mask(qlen, mlen, same_length=False):
attn_mask = tf.ones([qlen, qlen])
mask_u = tf.matrix_band_part(attn_mask, 0, -1)
mask_dia = tf.matrix_band_part(attn_mask, 0, 0)
attn_mask_pad = tf.zeros([qlen, mlen])
ret = tf.concat([attn_mask_pad, mask_u - mask_dia], 1)
if same_length:
mask_l = tf.matrix_band_part(attn_mask, -1, 0)
ret = tf.concat([ret[:, :qlen] + mask_l - mask_dia, ret[:, qlen:]], 1)
return retattention mask有两种形式
- 如果生成如图(a)所示的mask,那么$t+1$时刻的segment的第$j$个位置($j=1,\cdots,q\_len$),在计算attention score时,会使用在它之前的$(m\_len+j)$个位置的信息(包括其自身),对应代码中
same_length为false的情况; - 如果生成如图(b)所示的mask,那么$t+1$时刻的segment的第$j$个位置($j=1,\cdots,q\_len$),在计算attention score时,只会使用在它之前的$(m\_len+1)$个位置的信息(包括其自身),对于任意的$j$都是一样的,对应代码中
same_length为true的情况。
传统的做法都将每一个单词表示为长度相等的向量,当单词的量很大时,需要大量的存储空间,此外,不同的单词的重要程度不同,且所表达语义的丰富程度不同,对于一些简单的单词,可能只需要长度较短的向量就可以很好地表征它们的语义,而对于一些能表达更丰富语义的单词或者是更重要的单词(比如一些高频词,高频的词的一词多义的现象更加明显),可以使用较长的向量对其进行表示。 对于一个数据量较大的语料库,往往较少的高频词就能覆盖大部分的句子。因此,在模型的训练过程中,高频词会经常被更新,而低频词被更新的次数屈指可数。基于这一点,我们希望更新单词的embedding时,低频的词应该使用更少的资源,而高频的词可以增加一些资源(这里的资源尤指维度)。论文《Adaptive input representations for neural language modeling》基于这一思想提出了`adaptive representation`算法。adaptive Representation 将vocabulary中的单词但出现的频率从高到低排列,并划分为多个集合,较小序号的集合中,单词的频率较高。集合内的单词维度相同,集合间单词的维度不同,集合序号越大,维度越小设置 ,第n个集合的维度为$\frac{d}{k^n} (k = 4)$,其中n为列表序号(从0开始),d为原始维度。 transformer-xl中也采用了adaptive representation算法。 其中,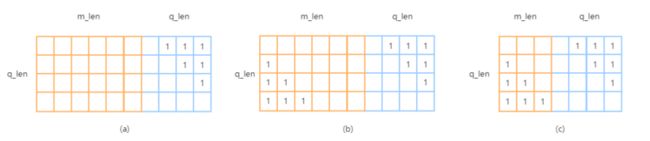
需要注意的是,当same_length为true时,使用代码ret=tf.concat([ret[:, :qlen] + mask_l - mask_dia, ret[:, qlen:]], 1)生成mask,是为了同时考虑m_len>=q_len(对应图(b))和m_lenadaptive embedding
def mask_adaptive_embedding_lookup(x, n_token, d_embed, d_proj, cutoffs, initializer,
proj_initializer, div_val=1,
proj_same_dim=True,
scope='adaptive_embed', **kwargs):
emb_scale = d_proj ** 0.5
with tf.variable_scope(scope):
if div_val == 1:
lookup_table = tf.get_variable('lookup_table', [n_token, d_embed],
initializer=initializer)
y = embedding_lookup(lookup_table, x, use_tpu=False)
if d_proj != d_embed: # hidden state的维度与embedding的维度不等
proj_W = tf.get_variable('proj_W', [d_embed, d_proj],
initializer=proj_initializer)
y = tf.einsum('ibe,ed->ibd', y, proj_W)
else:
proj_W = None
ret_params = [lookup_table, proj_W]
else:
tables, projs = [], []
cutoff_ends = [0] + cutoffs + [n_token]
x_size = tf.shape(x)
y = tf.zeros([x_size[0], x_size[1], d_proj]) # [len, bsz, d_proj]
for i in range(len(cutoff_ends) - 1):
with tf.variable_scope('cutoff_{}'.format(i)):
l_idx, r_idx = cutoff_ends[i], cutoff_ends[i + 1]
mask = (x >= l_idx) & (x < r_idx) # 按位与
cur_x = tf.boolean_mask(x, mask) - l_idx # 下标从0开始
cur_d_embed = d_embed // (div_val ** i)
# 注意,每一个lookup_table是在cutoff_{i}空间下的,所以是不一样的
lookup_table = tf.get_variable('lookup_table',
[r_idx - l_idx, cur_d_embed],
initializer=initializer)
cur_y = embedding_lookup(lookup_table, cur_x, use_tpu=False)
if d_proj == cur_d_embed and not proj_same_dim:
proj_W = None
else:
proj_W = tf.get_variable('proj_W', [cur_d_embed, d_proj],
initializer=proj_initializer)
cur_y = tf.einsum('id,de->ie', cur_y, proj_W)
mask_idx = tf.to_int64(tf.where(mask)) # mask中为1的位置坐标,
y += tf.scatter_nd(mask_idx, cur_y, tf.to_int64(tf.shape(y)))
tables.append(lookup_table)
projs.append(proj_W)
ret_params = [tables, projs]
y *= emb_scale # [seq_len, bsz, d_proj]
return y, ret_paramscutoff_ends表示集合划分的切分点,第i个集合的下标大于等于cutoff_ends[i],小于cutoff_ends[i+1],第i个集合对应的embedding 维度为 cur_d_embed = d_embed // (div_val ** i),对应的embedding lookup table为 lookup_table=tf.get_variable('lookup_table', [r_idx - l_idx, cur_d_embed], initializer=initializer),对于一个segment中的len个单词,其embedding的长度是不一样的,所以需要使用一个projection layer,进行维度变换,使得维度相同,proj_W = tf.get_variable('proj_W', [cur_d_embed, d_proj], initializer=proj_initializer) cur_y = tf.einsum('id,de->ie', cur_y, proj_W)。
给定一个输入x,维度为[len,bsz],len为一个segment的长度,bsz为batch size,为了查找第i个集合中的单词,首先使用位运算mask = (x >= l_idx) & (x < r_idx),得到shape为[len,bsz]的mask,元素为true表示当前位置对应的单词在第i个集合中,否则不在,接着使用cur_x = tf.boolean_mask(x, mask) - l_idx得到一个一维序列,方便使用embeding lookup进行表示,假设一共有n个集合,就会得到n组长度不同的embedding,对其进行拼接,使用tf.scatter_nd函数,它的作用是Scatter updates into a new tensor according to indices。一个简化版的案例如下, d_embed = 4
len = 3
bsz = 2
x = np.arange(1, len*bsz+1).reshape(len, bsz)
l_idx = 2
r_idx = 5
mask = (x >= l_idx) & (x < r_idx)
cur_x = tf.boolean_mask(x, mask) - l_idx
lookup_table = tf.get_variable("lookup_table", shape=[r_idx-l_idx, d_embed], initializer=tf.random_normal_initializer)
cur_y = tf.nn.embedding_lookup(lookup_table, cur_x)
y_shape = tf.zeros(shape=[len, bsz, d_embed])
y = tf.scatter_nd(indices=tf.where(mask), updates=cur_y, shape=tf.to_int64(tf.shape(y_shape)))
print("x: ", x)
print("mask: ", mask)
print("cur_x: ", cur_x)
print("cur_y:", cur_y)
print("y: ", y)
输出:
x: [[1 2]
[3 4]
[5 6]]
mask: [[False True]
[ True True]
[False False]]
cur_x: tf.Tensor([0 1 2], shape=(3,), dtype=int32)
cur_y: tf.Tensor(
[[-2.7328973 -0.01377826 -0.78023756 -1.1186032 ]
[-1.7653402 -0.8459847 -0.3368531 -0.27648798]
[ 0.2573444 1.1644957 1.0869092 1.3614684 ]], shape=(3, 4), dtype=float32)
y: tf.Tensor(
[[[ 0. 0. 0. 0. ]
[-2.7328973 -0.01377826 -0.78023756 -1.1186032 ]]
[[-1.7653402 -0.8459847 -0.3368531 -0.27648798]
[ 0.2573444 1.1644957 1.0869092 1.3614684 ]]
[[ 0. 0. 0. 0. ]
[ 0. 0. 0. 0. ]]], shape=(3, 2, 4), dtype=float32)参考