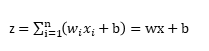从一组看似混乱的数据中找出y≈2x的规律

一 实例描述

假设有一组数据集，其中x和y的对应关系为出y≈2x。

本实例就是让神经网络学习这些样本，并能够找到其中的规律，即让神经网络能够总结出y≈2x这样的公式。

二 深度学习的4个步骤

1 准备数据

2 搭建模型

3 迭代训练

4 使用模型

准备数据阶段一般就是把任务相关数据收集起来，然后建立网络模型，通过一定的迭代训练让网络学习到收集来的数据特征，形成可用的模型，之后就是使用模型来为我们解决问题。

三 准备数据

这里使用y=2x这个公式来做主体，通过加入一些干扰噪声让它的“等号”变成“约等于”。

1 代码算法

1.1 导入头文件，然后生成-1~1之间的100个数作为x

1.2 将x乘以2，再加上一个[-1,1]区间的随机数×0.3。即，y≈2×x+ax0.3（a属于[-1,1]之间的随机数）。

2 代码

import tensorflow as tf
import numpy as np
import matplotlib.pyplot as plt

#生成模拟数据
train_X = np.linspace(-1, 1, 100)
train_Y = 2 * train_X + np.random.randn(*train_X.shape) * 0.3 # y=2x，但是加入了噪声
#显示模拟数据点
plt.plot(train_X, train_Y, 'ro', label='Original data')
plt.legend()
plt.show()

3 运行结果

四 搭建模型

1 正向搭建模型

1.1 正向模型及公式

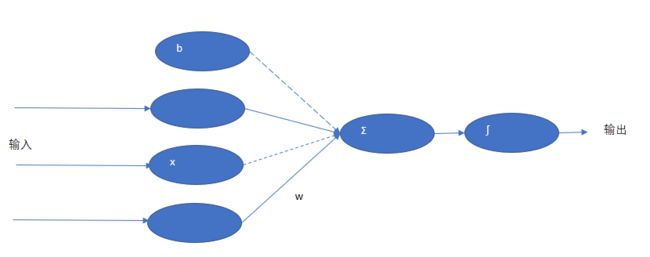
神经网络是由多个神经元组成的，单个神经元的网络模型如下图：

计算公式如下：

公式中，z为输出的结果，x为输入，w为权重，b为偏执值。

z的计算过程是将输入的x与对应的w相乘，然后再把结果加上偏执b。

在神经元中，w和b可以理解为两个变量。模型每次学习都是调整w和b以得到一个更适合的值。最终，有这个值配合上运算公式所形成的逻辑就是神经元网络的模型。

1.2 创建模型代码

# 创建模型
# 占位符
X = tf.placeholder("float")
Y = tf.placeholder("float")
# 模型参数
W = tf.Variable(tf.random_normal([1]), name="weight")
b = tf.Variable(tf.zeros([1]), name="bias")
# 前向结构
z = tf.multiply(X, W)+ b

1.3 解释

X和Y：为占位符，使用了placeholder函数进行定义。一个代表x的输入，一个代表对应的真实值y。

W和b：就是前面说的参数。W被初始化成[-1,1]的随机数，b初始化为0。

Variable：定义变量

tf.multiply：两个数相乘，结果再加上b就等于z了。

2 反向搭建模型

神经网络在训练的过程中数据的流向有两个方向，即先通过正向生成一个值，然后观察与其真实值的差距，再通过反向过程将里面的参数进行调整，接着再次正向生成预测值和真实值进行比对，这样循环下去，直到将参数调整为合适的值为止。

反向传播会引用一些算法来实现对参数的正确调整。

2.1 代码

#反向优化
cost =tf.reduce_mean( tf.square(Y - z))
learning_rate = 0.01
optimizer = tf.train.GradientDescentOptimizer(learning_rate).minimize(cost) #Gradient descent

2.2 代码说明

cost：它等于生成值与真实值的平方差。

learning_rate：定义了一个学习率，代表调整参数的速度。

GradientDescentOptimizer函数是一个封装好的梯度下降算法。

五 迭代训练模型

1 训练模型

建立好模型后，可以通过迭代来训练模型。TensorFlow中的任务是通过session来进行的。

下面的代码中，先进行全局初始化，然后设置训练迭代的次数，启动session开始运行任务。

# 初始化变量
init = tf.global_variables_initializer()
# 训练参数
training_epochs = 20
display_step = 2
# 启动session
with tf.Session() as sess:
    sess.run(init)
    # Fit all training data
    for epoch in range(training_epochs):
        for (x, y) in zip(train_X, train_Y):
            sess.run(optimizer, feed_dict={X: x, Y: y})
        #显示训练中的详细信息
        if epoch % display_step == 0:
            loss = sess.run(cost, feed_dict={X: train_X, Y:train_Y})
            print ("Epoch:", epoch+1, "cost=", loss,"W=", sess.run(W), "b=", sess.run(b))
            if not (loss == "NA" ):
                plotdata["batchsize"].append(epoch)
                plotdata["loss"].append(loss)
    print (" Finished!")
    print ("cost=", sess.run(cost, feed_dict={X: train_X, Y: train_Y}), "W=", sess.run(W), "b=", sess.run(b))
    #print ("cost:",cost.eval({X: train_X, Y: train_Y}))

上面代码中迭代次数设置为20次，通过sess.run来进行网络节点的运算，通过feed机制将真实数据灌到占位符对应的位置（feed_dict={X: train_X, Y:train_Y}），同时，每执行一次都会将网络中的节点打印出来。

运行代码，输出信息如下：

Epoch: 1 cost= 0.562266 W= [ 0.86304104] b= [ 0.3207536]
Epoch: 3 cost= 0.115723 W= [ 1.63402164] b= [ 0.1157342]
Epoch: 5 cost= 0.0768646 W= [ 1.84325504] b= [ 0.03697061]
Epoch: 7 cost= 0.0736684 W= [ 1.89752293] b= [ 0.01617121]
Epoch: 9 cost= 0.0733086 W= [ 1.91155732] b= [ 0.01078599]
Epoch: 11 cost= 0.0732468 W= [ 1.91518724] b= [ 0.00939313]
Epoch: 13 cost= 0.0732329 W= [ 1.91612494] b= [ 0.00903324]
Epoch: 15 cost= 0.0732294 W= [ 1.91636765] b= [ 0.00894016]
Epoch: 17 cost= 0.0732286 W= [ 1.91643071] b= [ 0.00891594]
Epoch: 19 cost= 0.0732283 W= [ 1.91644669] b= [ 0.00890978]
Finished!
cost= 0.0732283 W= [ 1.91644931] b= [ 0.00890878]

可以看出，cost的值在不断地变小，w和b的值也在不断地调整。

2 训练模型可视化

为了得到更直观的表达，下面将模型中两个信息可视化出来，一个是生成的模型，另一个是训练中的状态值。具体代码如下：

#图形显示
    plt.plot(train_X, train_Y, 'ro', label='Original data')
    plt.plot(train_X, sess.run(W) * train_X + sess.run(b), label='Fitted line')
    plt.legend()
    plt.show()
    
    plotdata["avgloss"] = moving_average(plotdata["loss"])
    plt.figure(1)
    plt.subplot(211)
    plt.plot(plotdata["batchsize"], plotdata["avgloss"], 'b--')
    plt.xlabel('Minibatch number')
    plt.ylabel('Loss')
    plt.title('Minibatch run vs. Training loss')
     
    plt.show()

这段代码引入了一个变量和一个函数，可以在代码的最顶端定义它们，见下面代码：

plotdata = { "batchsize":[], "loss":[] }
def moving_average(a, w=10):
    if len(a) < w:
        return a[:]    
    return [val if idx < w else sum(a[(idx-w):idx])/w for idx, val in enumerate(a)]

现在所有代码都准备好了，运行程序，生成结果如下：

从运行结果可以看到：所示的斜线，是模型中的参数w和b为常量所组成的关于x与y的直线方程。可以看到几乎是一个y=2x的直线（W=1.91644931接近2，b=0.00890878接近于0）。

从中可以看出刚开始损失值一直在下降，直到6次左右趋于平稳定。

六 使用模型

模型训练好后，用起来就比较容易了，往里面传入一个0.2（通过feed_dict={X: 0.2})，然后使用sess.run来运行模型中的z节点，见下面代码，看看它的生成的值。

    print ("x=0.2，z=", sess.run(z, feed_dict={X: 0.2}))

运行后，可以得到如下信息：

x=0.2，z= [ 0.39219865]

训练好后的模型，可以根据已有数据的规律推算出输入0.2对应的z值。