最形象的讲解，让你一次学会什么叫LCA离线算法tarjan

今天刚学了LCA离线tarjan算法。下面跟大家分享一下我的学习心得。
首先LCA是Lowest Common Ancestors的缩写。中文名为最近公共祖先。然后就是什么叫离线，与离线相对应的是在线算法（用dfs + rmp）的区别在哪里。
离线算法就是把所有的询问存起来，最后一次解决输出结果。结果有可能需要所有的询问（更新）之后才能得到。
在线算法就是每次询问一次，输出询问结果，每次的结果只与这次的询问有关，与其他询问无关。
我在这里先讲一下离线的tanjan算法，我会陆续的学习在线算法，到时候也会写一篇博客，欢迎大家一起学习，讨论。
tanjan算法是基于并查集实现的，如果还有萌新不知道什么叫并查集，那么请先去学习有关并查集的知识，不然可能会不懂这个tanjan算法。
那么下面我就着重说一下tanjan算法具体是怎样实现的。
首先我们把树上所有的节点的父亲设置成这个节点本身。我们用father[i]表示节点i的父亲，所以这个用代码实现就是

for(int i = 1; i <= n; i++)
{
   father[i] = i;
}

做完之后首先找到整棵树的根节点root，我们从跟节点开始dfs.
dfs的过程是
1.首先判断有没有询问与这个点有关，比如当前dfs到了u这个点，有一个询问是与u有关的，比如其中的一个询问是询问u与点v的最近公共祖先。
那么我们先判断一下v是否已经被访问过，如果被访问过，则u,v的最近公共祖先就是lca = Find（v）；其中Find函数实现如下：

int Find(int x)
{
  if(x == father[x]) return father[x];
  else return father[x] = Find(father[x]);
}

如果v没有被访问则直接执行以下步骤：
2.visit[u] = true；
3.dfs u的每一个儿子节点，比如u有一个儿子son，那么先dfs(son），dfs完了之后把son的父亲置为u。（刚开始son的父亲是自己，这个在初始化时已经做完了）
上面所以的实现可以用以下代码表示，其中LCA[i][j] 表示i与j的最近公共祖先。ask[i][j]表示要询问i与j的最近公共祖先,g[i]表示i的儿子向量。

void dfs(int u)
{
   for（int i = 1; i <= n; i++)
   {
      if(visit[i]&&ask[u][i])
      {
        LCA[u][i] = Find(i);
      }
   }
   visit[u] = true;
   for(int i = 0; i < g[u].size(); i++)
   {
     int son = g[u][i];
     dfs(son);
     father[son] = u;
   }
}

可能看了上面的文字讲解和代码实现，你还是有一种似懂非懂的感觉，可能会产生这样一个疑问，为什么这样做是对的?为什么这样做就能求出两个点的最近公共祖先？产生了这样的疑问是好事，说明你在思考，而不是强行记模板。下面我用两张图来简单的说一下为什么这样做就能求出两个点最近公共祖先。
对于任意两个点(u,v),只能有两种情况1.v是u的一个儿子，或者说v在以u为根节点的子树中（或者反过来u是v的儿子，都是一个道理，我们这里为了方便，就假设v是u的儿子（可能不是直接儿子））
2.u,v没有儿子关系

对于第一种情况假如如下图：

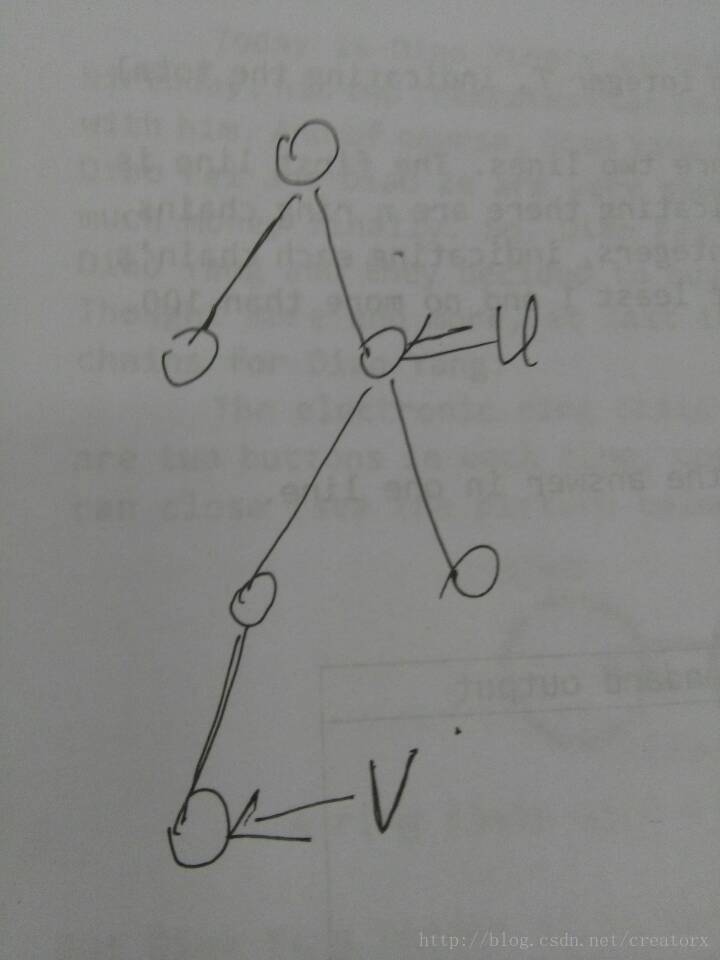
根据dfs的性质可知，首先dfs到点u,这时发现有一个询问是关于u，v的，但是此时v还没有被访问到，所以在这里先不做处理，继续往下dfs，注意此时虽然u点已经被访问到了，但是father[u]还是u，因为以u为根的整棵子树还没有访问完。然后当dfs到了v时，发现有一个询问是关于v,u的然后判断u有没有被访问，很显然此时u早已经被访问所以LCA[v][u] = Find(u) = u;
对于第二中情况假如如下图：

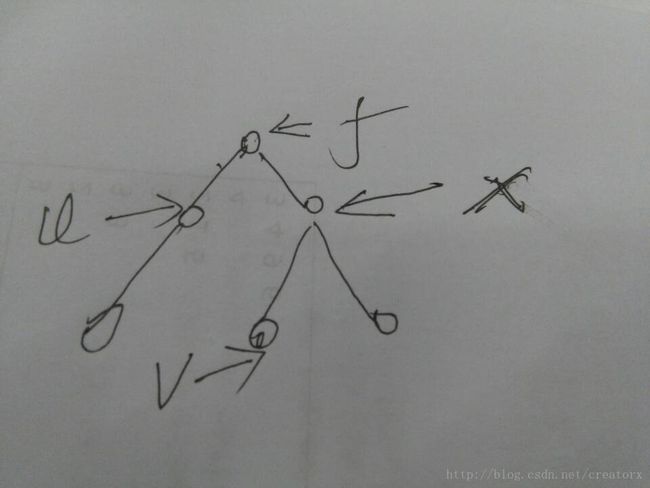
根据dfs的性质,有可能先访问到u,也有可能先访问到v。所以我们可以分为两种情况讨论。
1.先访问到v
当访问到v时，因为u还没有被访问，所以不做处理，当访问完v之后father[v] = x,如图，然后father[x] = f,然后访问到u,这时发现v已经被访问过了，所以LCA(u,v) = Find(v) = Find(x) = Find(f) = f.

2.先访问到u.
当访问到u时，因为v还没有被访问,所以不做处理，当访问完以u为根的子树后，father[u] = f;然后访问x,然后访问v.当访问到v时，发现u已经被访问了,所以LCA(v,u) = Find(u) = f;

至此，上面两种情况已经讨论完了，你现在应该已经明白了为什么这样做是对的的原因。

那么理论知识我们学习完了，我们下面去实践一下，我们以poj1470为例。
ac代码如下：

#include
#include
#include
#include
#include
using namespace std;
const int maxn = 1000;
int ask[maxn][maxn];//保存询问
int ans[maxn];//保存祖先i出现过的次数
int n,m;
vector<int> g[maxn];//保存儿子
int root;//树的根
bool visit[maxn];
bool isroot[maxn];
int father[maxn];
int Find(int x)
{
    if(father[x] == x) return x;
    else return father[x] = Find(father[x]);
}
void init()
{
    memset(ans,0,sizeof(ans));
    memset(visit,false,sizeof(visit));
    memset(isroot,true,sizeof(isroot));
    memset(ask,0,sizeof(ask));
    for(int i = 1; i <= n; i++)
    {
        g[i].clear();
        father[i] = i;
    }

}
void LCA(int root)
{
    for(int i = 1; i <= n; i++)
    {
        if(visit[i]&&ask[root][i])
        {
            ans[Find(i)] += ask[root][i];
        }
    }
    visit[root] = true;
    for(int i = 0; i < g[root].size(); i++)
    {
        int term = g[root][i];
        LCA(term);
        father[term] = root;
    }
}
int main()
{
    while(~scanf("%d",&n))
    {
        init();
        int f,s,num;
        for(int i = 1; i <= n; i++)
        {
            scanf("%d:(%d)",&f,&num);
            for(int j = 1; j <= num; j++)
            {
                scanf(" %d",&s);
                isroot[s] = false;
                g[f].push_back(s);
            }
        }
        for(int i = 1; i <= n; i++)
        {
            if(isroot[i])
            {
                root = i;
                break;
            }
        }
        scanf("%d",&m);
        int u,v;
        for(int i = 1; i <= m; i++)
        {
            scanf(" (%d %d)",&u,&v);
            ask[u][v]++;
            ask[v][u]++;
        }
        LCA(root);
        for(int i = 1; i <= n; i++)
        {
            if(ans[i])
            {
                printf("%d:%d\n",i,ans[i]);
            }
        }
    }
    return 0;
}

以上就是我今天学了一上午的LCA离线tarjan算法的心得，希望对大家有用，如果上面有什么不对的地方，欢迎各位大佬指出.