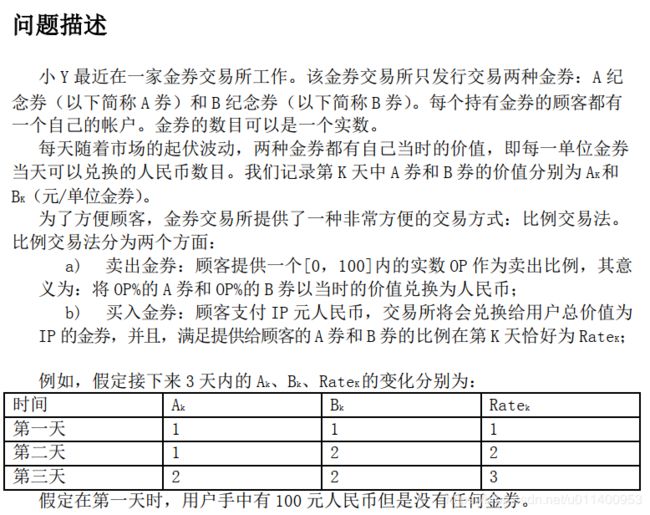
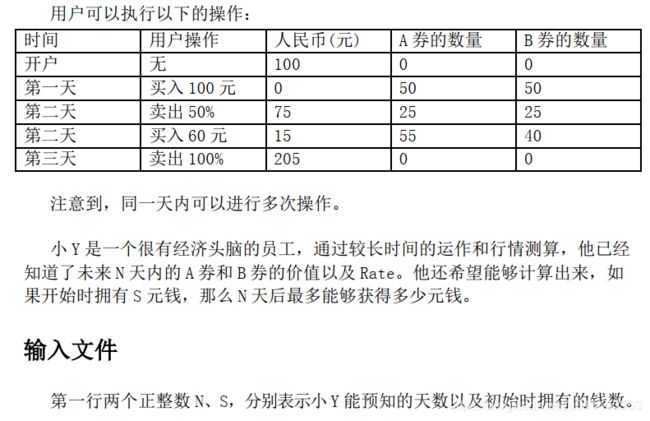
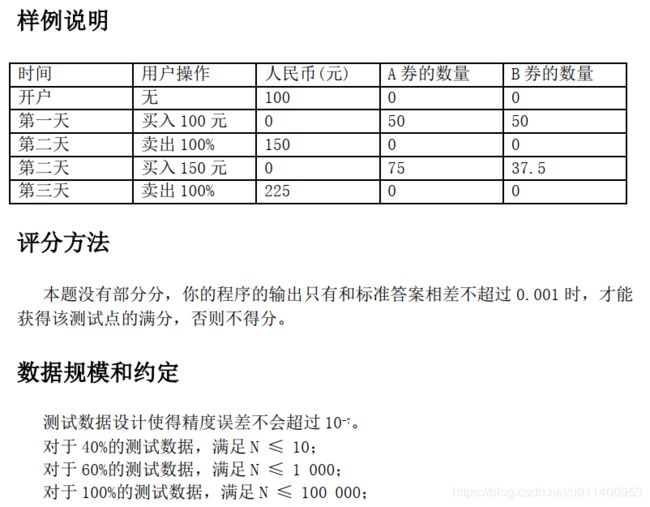
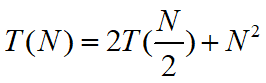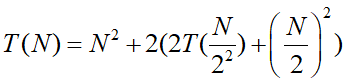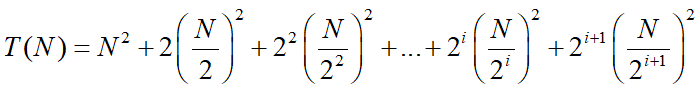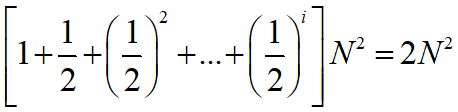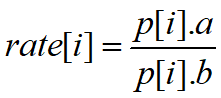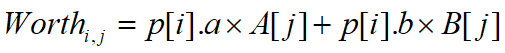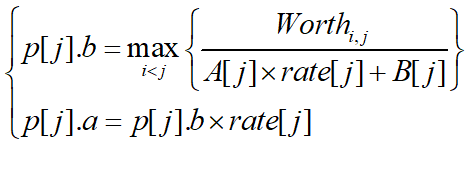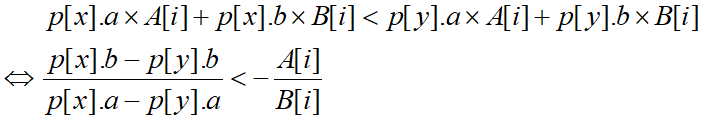CDQ分治（含例题：货币兑换、PARTIAL ORDER）

最近在整理原来的一些资料，偶然想起原来搞OI时讲过一次CDQ分治的内容，这里分享给大家

 

目录

预备知识

常见递归复杂度

分治思想

CDQ分治例题

货币兑换

PARTIAL ORDER

问题2D版本

问题3D版本

问题4D简化版本

问题4D版本

问题100D版本

总结

题目推荐

---

CDQ分治是一种特殊的分治方法，在OI界初见于陈丹琦2008年国家集训队作业中

 

预备知识

常见递归复杂度

先来分析下面这个递归方程：

其时间复杂度如何分析？

将式子迭代两次得：

 

继续迭代，整理得：

 

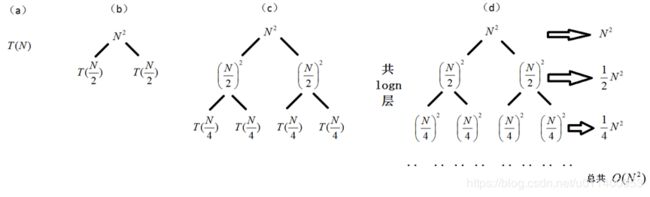
我们发现式子的结构特别像一个树形结构，由此可引出递归树法：

图中的(a)(b)(c)(d)分别是递归树生成的第1,2,3...N步。每一节点中都将当前的自由项n^2留在其中，而将两个递归项T(n/2) + T(n/2)分别摊给了他的两个子节点，如此循环。

图中所有节点之和为:

因此原递归方程的时间复杂度为O(n^2)

可以得到递归树法的规则为：

  (1) 每层的节点为T(n) = kT(n / m) + f(n)中的f(n)在当前的n/m下的值；

  (2) 每个节点的分支数为k；

  (3) 每层的右侧标出当前层中所有节点的和。

 

那么通过该方法，可以推出这些式子：

• T(n)=2T(n/2)+O(kn)的解是T(n)=O(kn log n)
• T(n)=2T(n/2)+O(kn log n)的解是T(n)=O(kn log^2n)
• T(n)=2T(n/2)+O(k)的解是T(n)=O(kn)        

 

分治思想

问题：给定序列Ai，求序列中的逆序对数

 

方法：归并排序实现：定义归并排序过程Merge(l,r)

Merge(l,r)

¤Merge(l,mid)

¤Merge(mid+1,r)

¤Count(l,mid,mid+1,r)

由于之前已执行过merge(1,mid)，那么[l,mid]之间的元素是有序的，因此若i∈[l,mid],j∈[mid+1,r]，若有a[i]>a[j]成立，则答案加上mid-i+1

 

CDQ分治例题

货币兑换

此题为NOI2007一试第二题

其实解决这个问题的突破口在提示：

设f[i]表示第i天全部将A,B券换成人民币的最多数目，p[i].a表示A券在第i天最多拥有的个数，p[i].b表示B券在第i天最多拥有的个数，则：

那么，对于第i天最后一次购买，它在第j天（i）的折合人民币就是：

于是：

因此，我们得到一个动态规划的算法，框架如下：

p[1].b=S / (A[1] * Rate[1] + B [1]) 
Ans=S
For  i = 2  to  n ← 枚举在哪一天卖出券
       For  j = 1  to  i-1   ← 枚举在哪一天买入券
               x=p[ j ].a * A[i ] + p[j ].b * B [i ]
              Ans=max{Ans,x}
       End For
       p [i ].b = Ans / (A[i ] * Rate[i ] + B[i ])
End For
Print(Ans)

我们可以把最后一次购入金劵的时间看作一种决策。现在考虑两种不同的决策在此时哪种能够获得最大的折合人民币。假设第i天A劵的价值为A[i]，B劵的价值为B[i]，两个不同的决策是：最后一次在第x天和第y天买入金劵。那么，决策x不如决策y优等价于：

这样我们就可以用平衡树以p[j ].a为关键字来维护一个凸线，平衡树维护一个点集(p[j ].a, p[j ].b)，p[j ].a是单调递增的，相邻两个点的斜率是单调递减的．每次在平衡树中二分查找与-A[i ] / B[i ]最接近的两点之间的斜率

这样其实就转化成了斜率优化的动态规划

可是用平衡树维护，编程复杂度高了

 

事实上，我们可以利用分治的思想来提出一个编程复杂度比较低的方法：

首先我们按斜率-A[i]/B[i]从小到大排序，对于每一个i，它的决策j 的范围为1~i-1；我们定义一个Solve过程：Solve(l, r )

设mid=(l+r)/2，类似归并排序，我们用[l,r]的前半部[l,mid]，来更新[l,r]区间的后半部[mid+1,r]的答案值，即在第i天我能得到的最大人民币数值，其中i∈[mid+1,r]

对于当前处理的区间[l,r]，我们可以先Solve(l, mid )，这样保证在区间[l,mid]内的所有答案值均已被更新

然后对该区间的前半部建立一个凸壳（凸线），对于参与建立凸壳的点，需保证其水平序有序；用这个凸壳（凸线）去更新这个区间的后半部，其中后半部的所有元素，其-A[i]/B[i]，即斜率，均有序，而凸壳的斜率也是单调的，这样正好可以用来解决本区间后半部的答案更新问题

而前半部分的排序只需在每次某区间全部处理完毕后，将该区间的所有元素<即将前半部分和后半部分合并>按水平序排序即可，后半部的元素在整个solve过程之前已整体按斜率排过一遍序

注意到，对于一个区间的前半部和后半部的作用是不同的，前半部的元素的答案值均已更新过答案值，为后半部的更新提供凸壳，后半部的元素的答案值更新由前半部构造的凸壳来更新答案，两部分的顺序互不影响。这样，我们只需要保证前半部的元素按水平序排序，后半部分按斜率排序，这样就相当于用一系列连续的直线去切一些连续点组成的凸壳。

给出一个算法框架：

Procedure Solve(l, r)
If l = r Then
    直接更新答案值
Exit
Solve(l, mid )
→对[l, mid ]这一段扫描一遍计算出凸线
→扫描一遍更新[mid +1 , r]的最优决策
→ Solve(mid+1, r)
→将两部分合并，按水平序排序　
 End Procedure

时间复杂度分析：递归主过程：构造凸壳以及更新答案： O(n)，那么递归方程为：T(n)=2T(n/2)+O(n)，即时间复杂度为O(nlogn)

 

从这个例题中，我们可以看出，其solve过程的实质为：

       →Solve(L,middle)

       →处理[L,middle]中元素对[middle+1,R]中f[x]取值的影响

       → Solve(middle+1,R)

而在该问题中，处理影响部分相当于是更新答案值部分；使用了维护凸壳，斜率DP等方法来在尽可能优的时间内更新答案

 

附代码：

#include
#include
#include
#include
#include
#include
using namespace std;
#define MAXN 100001
#define EPS 1e-7
#define IMAX 21474836.0
struct DAY{double a,b,rate,k;int num;}a[MAXN],use[MAXN];
struct MONEY{double a,b;}p[MAXN],tmp[MAXN];
int N,stack[MAXN];
double S,f[MAXN];
bool cmp1(DAY X,DAY Y){return X.kright) && L1<=middle)
                  tmp[i]=p[L1++];
            else  tmp[i]=p[L2++];
      }
      for(int i=left;i<=right;i++)
            p[i]=tmp[i];      
}
void solve(int left,int right)
{
      if(left==right)
      {
            if(left==1)   f[left]=f[left]=1 && getk(i,stack[top])>getk(stack[top],stack[top-1]))
                  top--;
            stack[++top]=i;
      }
      for(int i=right;i>=middle+1;i--)
      {
            while(now+1<=top && (a[i].k

 

PARTIAL ORDER

在开始这个问题之前，需要说明的是，接下来是一系列相关问题，对于每个问题不一定要用CDQ分治解决

问题2D版本

有N个人，每个人有一种能力值Pi,Qi。如果Pi>Pj && Qi>Qj，称i比j有能力。现在要求出最长的一个序列长度A=(A1,A2,…,At)，满足Ai比Ai+1有能力。N<=100000，为了简单起见，P、Q都是1到N的排列。

方法：把人按照Pi排序，问题变为求序列Qi的最长上升子序列。动态规划方程：F[i] = Max({F[j] | j

 

问题3D版本

有N个人，每个人有三种能力值分别为Pi , Qi , Ri，如果有Pi>Pj , Qi>Qj , Ri > Rj 成立，则称i比j优秀。现在要求求出最长的序列长度A，满足Ai比Ai+1优秀。N<=40000。为了简单起见，P,Q,R都是1到n的排列

思考：首先我们可以按照Pi把人从小到大排个序，问题转化为求满足i

“推荐”算法：线段树套平衡树，时间复杂度：O(nlog^2n)

呵呵~

 

考虑使用分治的思想来优化

定义函数solve(L,R)，能够得到f[L]...f[R]的值，其大致框架为：

     →Solve(L,middle)

     →处理[L,middle]中元素对[middle+1,R]中f[x]取值的影响

     → Solve(middle+1,R)

那么对于方程：

如果i在区间[L,middle]中，那么可以递归处理；如果i在区间[middle+1,R]中，那么可以通过处理影响来解决

之前已对P值排过序，把该区间的前半部分当成带权点集X=(Qi,Ri)，其权值为f[i]；对于后半部分，相当于考虑给定一点(Qj,Rj)，在点集X中寻找一个点(Qi,Ri)，使得Qi>Qj ,Ri>Rj；在所有满足以上条件的点中取权值最大的

整理一下思路，当前P值的条件已经符合要求，现在需考虑Q，R满足要求。

我们可以对其中一个属性(P或Q)排序，相当于固定住一个属性，保证其单调，然后可以对另一个属性构造权值线段树，其在树中位置即为属性值，权值即为此点的权值f[i]。注意，“此点”指的是点集X中的点，这样，该问题圆满解决。

此问题中，“处理影响”部分使用了线段树和排序的方法来保证在尽可能优的时间内更新答案，时间复杂度

¤T(n)=2T(n/2)+O(nlogn)

¤T(n)=O(nlog^2n)

附3D版本程序：

#include
#include
#include
#include
#include
#include
using namespace std;
#define MAXN 100010
#define MAX 200000
struct STUDENT{int q,w,e,num;}a[MAXN],tmp1[MAXN],tmp2[MAXN];
int N,M,data[MAXN],ANS,ans[MAXN],S[MAX],DATA=0;
bool cmp1(STUDENT X,STUDENT Y){return X.q>=1;now;now>>=1)
            S[now]=max(S[2*now],S[2*now+1]);
}
int getmax(int left,int right)
{
      if(left>right)   return 0;
      int nowans=0;
      for(left+=M-1,right+=M+1;left^right^1;left>>=1,right>>=1)
      {
            if(~left&1)   nowans=max(nowans,S[left^1]);
            if(right&1)   nowans=max(nowans,S[right^1]);
      }
      return nowans;
}
void solve(int left,int right)
{
      if(left==right)
            return;
      int middle=(left+right)/2,tmp1num=0,tmp2num=0;
      solve(left,middle);
      
      memset(S,0,sizeof(S));
      M=N;
      for(int i=left;i<=middle;i++)
            tmp1[++tmp1num]=a[i];
      for(int i=middle+1;i<=right;i++)
            tmp2[++tmp2num]=a[i];
      sort(tmp1+1,tmp1+1+tmp1num,cmp2);
      sort(tmp2+1,tmp2+1+tmp2num,cmp2);
      
      int tmp1now=1;
      for(int i=1;i<=tmp2num;i++)
      {
            while(tmp1[tmp1now].eans[i]?ANS:ans[i];
      printf("%d\n",ANS);
      return 0;
}

 

问题4D简化版本

有N个人，每个人有四种能力值Pi,Qi,Ri,Si。如果Pi>Pj && Qi>Qj && Ri>Rj && Si>Sj，称I比J有能力。对每一个人，输出任意一个比他有能力的人编号，或声明没有人比他有能力。N<=40000。简单起见，P,Q,R,S都是1-n的排列。

分析：首先把元素按Pi排序,这样相当于去掉了一维。对每个j，要判断是否有一个i满足j

 

问题4D版本

有N个人，每个人有四种能力值Pi,Qi,Ri,Si。如果Pi>Pj && Qi>Qj && Ri>Rj && Si>Sj，称I比J有能力。现在要求出最长的一个序列A=(A1,A2,…,At)，满足Ai比Ai+1有能力。N<=20000

分析：

树套树套树？？？十六分树？？？首先将元素按照Pi排序，用F[i]表示以第i个人结尾的最长序列，F[i] = Max{F[j] | j

¤树套树套树->TLE+MLE

¤Hash动态节点，三维树状数组……->？？？

 

我们尝试一下分治的思路：

定义Solve(l,r)， 能够得到f[l]...f[r]的值，其大致框架为：

¤→Solve(l,mid)

¤→考虑[l,mid]中的点对[mid+1,r]中答案值的影响

¤→ Solve(mid+1,r)

整体考虑

¤给定带权点集X=(Qi,Ri,Si) [l<=i<=mid]，权值为F[i]

¤给定询问<(r-mid)个>(Qj,Rj,Sj) [mid+1<=j<=r]

¤对于每个询问，回答点集中满足Qi的最大权值

离线操作

¤按Qi排序

¤询问满足Ri的点的最大权值

 

询问满足Ri<Rj,Si<Sj的最大权值

¤线段树套平衡树？

¤树状数组套平衡树？

 

再分治一次！

定义分治过程Solve2(l,r),用于处理Solve(l,r)中[l,mid]中的点对[mid+1,r]中F[]值的影响。

Solve2(l,r)

¤Solve2(l,mid)

¤处理(l,mid)中点对(mid+1,r)中询问的影响

¤Solve2(mid+1,r)

和Solve(l,r)有什么区别？

 

Solve(l,r)

¤→Solve(l,mid)

¤→创建一个[l,r]的副本并按照Q[i]排序

¤→ Solve2(l,r)

¤→ Solve(mid+1,r)

 

Solve2()的工作

        由于之前已对Q排序

¤维护带权点集X=(Ri,Si)，支持两个操作

¤1) 将一个点(Ri,Si)插入X，权值F[i] (l<=i<=mid)

¤2) 给出询问(Rj,Sj)，求一个权值最大且满足Ri的点

在Solve2()上定义分治过程

 

Solve2(l,r)

¤Solve2(l,mid)

¤处理[l,mid]的点对[mid+1,r]的询问的影响

¤Solve2(mid+1,r)

维护带权点集X=(Ri,Si) (l<=i<=mid)，权值F[i]

支持询问：给定点(Rj,Sj) (mid+1<=j<=r)

在点集X中寻找一个点(Ri,Si)使得Ri<Rj且Si<Sj，满足以上条件的点中取权值最大的。

 

离线处理

同3D情况，排序后树状数组或线段树维护

 

时间复杂度分析

定义T2(n)为Solve2(l,r)的时间复杂度

其递归方程为：

T2(n)=2T2(n/2)+O(nlogn)

T2(n)=O(nlog^2n)

定义T(n)为Solve(l,r)的时间复杂度

其递归方程为：

T(n)=2T(n/2)+T2(n)=2T(n/2)+O(nlog^2n)

则最终时间复杂度为：

T(n)=O(nlog^3n)

 

问题100D版本

有N个人，每个人有100种能力值P[i,1],P[i,2],...,P[i,100]。如果对于1<=k<=100有P[i,k]>P[j,k]，称I比J有能力。现在要求出最长的一个序列A=(A1,A2,…,At)，满足Ai比Ai+1有能力。N<=500。简单起见，P[x,1], P[x,2],..., P[x,100],都是1到n的排列

CDQ分治？→99个logn......

(树套树)^n?→......

脱离思维束缚！

考虑图论做法：枚举每对(i,j)，判断i是不是比j有能力，在构造出的图上求最长链

时间复杂度：O(100*n^2)

是不是很简单呢

 

总结

总结一下，CDQ分治是基于时间（或阶段、顺序）分治，牺牲部分时间复杂度，将问题离线化，将变化的问题转为不变。分治的递归过程用于解决段内问题，两段间问题由分治主过程解决，在特殊场合有很好的效果

优势：代码简短易读，效率不错，编程复杂度低，易于调试

劣势：递归过程导致常数变大，有时候需要去递归

CDQ分治在某些方面可以做到代替树套树这种结构，能够代替树套树的其实还有可持久化数据结构

 

题目推荐

NOI 2007 第一试 货币兑换 BZOJ 1492（参见：https://blog.csdn.net/csyzcyj/article/details/107299449）

POJ 1195（IOI 2001 mobiles）（参见：https://blog.csdn.net/csyzcyj/article/details/107300327）

BOI 2007 mokia（参见：https://blog.csdn.net/csyzcyj/article/details/107300159）

 

转载注明出处：https://blog.csdn.net/csyzcyj/