VoxelMorph

VoxelMorph

 

 

摘要

       之前的配准方法registration都是最优化一个目标函数optimize an objective function（每一对配准对象之间都是独立的），改论文的配准方法registration是通过定义一个参数化的函数parametric function，并且从给定的数据集中最优化该函数的参数optimize parameters。一对新的待配准图像可以通过使用学习得到的参数直接计算函数来获取配准域registration filed。CNN结构用于学习参数换函数、空间变换层用来将形变场运用到待配准图像上，同时加入了配准场的平滑约束，smoothness constraints on the registration filed。

• 引言

在形变配准中deformable registration，一对n维图像体n-D image volumes之间简历的密集非线性对应关系dense、non-linear。大多数的配准方法利用的是最优化的问题optimization，非常耗时。

该文提出的是从体集合a collection of volumes参数化配准函数parametrized registration function。该参数化函数使用卷积神经网络convolutional neural network(CNN)来训练，输入是两个n维体volumes，输出的话是从一个体到另一个体volumes所有体素voxels的映射。该网络的参数parameter，也就是卷积核的权重convolutional kernel weights，通过相关的数据集训练得到。通过该集合体collection of volumes参数的共享，可以对其任何一卷相同分布same distribution的新体对。本质上是使用一个全局的代价函数global function来替换每个测试图像对传统配准算法昂贵优化costly optimization of traditional registration algorithms for each test image pair。新的待配准图像直接在学习函数learned functon上进行配准。

1. 基于无监督学习的解决方案unsupervised learning-based solution。
2. 跨种群参数共享的CNN函数来评估配准。
3. 代价函数的参数最优化方法。

二、背景

      一般的配准流程volume registration formulation，就是一个卷（moving or source）volume通过扭曲对齐warped to align到第二个卷(fixed or target) volume。形变配准deformable registration将从普通的全局对其中先将放射变换分离出来，因为其他的形变配准要慢得多。

一般的配准算法registration algorithm都是通过迭代最优化能量函数energy function实现变换的。最优化的函数如下：

		(1)
		(2)

其中F是fixed image，M是moving image，是配准域registration field。是moving image， M使用形变场配准后的图像。用来衡量F和相似性的similarity，是对形变场ϕ进行正则化的regularization，是正则化参数regularization parameter。

      、、有几个共同的形式。一般是移动向量场displacement vector field，也就是从F图像到M图像每个体素voxle的矢量偏移量。微分同胚变换diffeomorphic transforms是一个较为常见的选择，将形变场作为一个速度向量场的积分integral of a vector field。因此他们可以保持拓扑结构topology并且执行可逆invertibility 。

      度量一般来说有均方体素差mean squared voxel difference, 交互信息mutual information 和互相关cross-correlation。交互信息mutual information和互相关cross-correlation在强度分布和对比度不一致时十分有效。

增强了一个空间平滑形变spatially smooth deformation，一般是采用空间梯度的线性操作linear operator on spatial gradients of

三、相关工作

3.1、基于非线性的医学图像配准

       在位移向量场的空间the space of displacement vector fields中的配准，主要有弹性模型elastic-type models， 统计参数映射statistical parametric mapping，b采样的自由度形式形变free-form deformations with b-splines，和Demons。本文的模型也是假设在位移向量场displacement vector fields。微分同胚变换Diffeomorphic transforms，可以保证拓扑结构topology-preserving，并且在各种计算解刨学研究上取得了显著效果。常用的公式包括：大差春距离度量映射Large Diffeomorphic Distance Metric Mapping(LDDMM)、DARTEL和标准对称归一化standard symmetric normalization(SyN)

3.2、基于学习的医学图像配准

       已经有一些论文提出了利用神经网络学习一个用于医学图像配准的函数，这些大多数依赖于扭曲域warp fields或者分割segmentations。这些提出的方法都是由一个CNN网络和空间变换函数组成spatial transformation function。但是这些提出的论文只是在3D子区域或者2D切片上做少量形变。另外的一些是用插值方法隐士的确定一些正则项的。相比而言，本文的方法适用于整个三维体，并且使用任意可微分的代价函数。

3.3、2D图像对齐

       光流估计optical flow estimation是一个与3维体类似的2维配准。光流算法optical flow algorithms返回一个描述2维图像对之间小位移的密集位移向量场a dense displacement vector field。传统的光流方法使用变分方法解决类似于（1）的优化问题。扩展的方法可以处理大的位移或外观变换包括基于特征匹配feature-based matching和最近邻域nearest neighbor fields的方法。

       一些用于2维图像对齐基于学习的方法被提出，一各是在自然图像中使用PCA学习低维基的方法。另一个是通过卷积神经网络convolutional neural network学习光流optical flow参数函数parametric function的方法。这些方法在训练的时候都是需要分割信息的。空间变换层spatial transform layer使得神经网络neural network能够在不需要监督标签supervised labels的情况下实现全局参数化global parametric的二维图像对齐aligment。

四、方法

       F、M是定义在n-D空间的两个图像体image volumes。本文是在3维空间。为了简化，假设F、M是单通道single-channel、灰度数据grayscale data。假定F、M在预处理阶段就已经仿射对齐了affinely aligned，仅剩下了非线性对齐操作。有很多的工具包可用于仿射对齐。

       本文的模型函数使用卷积神经网络convolutional neural network(CNN)求解，ϕ是配准域registration field，θ是函数g可学习到的参数learnable parameters。对于每个体素voxel p∈Ω，是形变场在位置p的位置，相似的、是相同的解刨学位置anatomical locations。

                                     图2 本文方法

       M和F是输入，计算基于参数θ的形变场ϕ，θ也是卷积层的核函数。将使用空间变换函数spatial transformation function扭曲到warp to  ，然后使用模型评估和图像F之间的相似性以更新参数θ。

       通过最小化损失函数loss function⋅利利用随机梯度下降方法找到最优参数optimal parameters

	(3)

D是数据集分布dataset distribution，通过在数据集D中的采样体对volume pairs对齐学习，这里不需要一些监督信息supervised information例如真是的配准域ground truth registration或者解刨学标记anatomical landmarks。在测试期间给定一个没有见过的M、F，我们将通过评估g以获得配准域registration field。

4.1 VoxelMorph CNN Architecture

g函数基于类似于UNet的卷积神经网络来实现参数化，网络由一些包含跳跃连接的编码器-解码器encoder-decoder组合而成，可以从给定的M和F中响应生成ϕ。

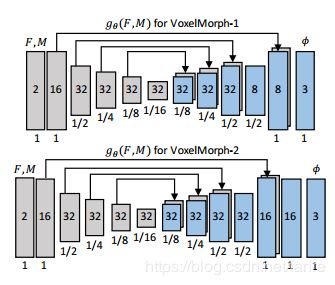
图3 卷积结构

图3描述了两种架构变体，一个是注重配准精度，另一个是注重配准的时间。两个网络的输入都是将M和F组成一个2通道的3D图像，在本论文实验中输入图像尺寸是160*192*224*2。在编码器和解码器阶段使用了三维卷积，之后势利眼Leaky ReLU激活函数，卷积核大小是3*3*3。在卷积层获取输入图像对的层次特征hierarchical features来评价相应的形变场ϕ。

在编码层encoder使用卷积步长strided convolutions来将空间维度减半，直到达到最小层。在输入图像的粗糙表示上随后的编码操作与传统的图像配准工作的图像金字塔image pyramid类似。

最小卷积层的接收域receptive fields至少应该与M和F中相应体素之间最大期望位移相同maximum expected displacement。最小层是输入图像尺寸的。解码层decoding stage，我们交替使用上采样upsampling,卷积层convolutions（Leaky ReLU激活层之后）并且连接跳跃concatenating skip connections。跳过连接skip connections将在编码阶段学到的特性直接传播到用于生成配准的层。编码器decoder的输出ϕ，在本文的输出尺寸是160*192*224*3。解码器的连续层操作在更精细的空间尺度上，使精确的解剖对齐成为可能。

4.2、Spatial Transformation Function

       该方法学习最优化参数的值一部分上是最小化和F之间的差异，为了使用标准的基于梯度方法standard gradient-based methods，构建了基于空间变换网络spatial transformer network的可微分方法来计算。

       对于每个体素voxel p，我们计算出了M的一个亚像素体素位置subpixel voxel location ，但是由于图像位置必须是整数，我们在8个领域体素eight neighboring voxels使用线性插值linearly interpolate方法，形式如下：

(4)

是的邻域voxel neighbors，因为操作在任意位置是可微分的，因此我们可以在最优化期间反向传播backpropagate误差。

4.3、损失函数

       提出的方法在可微的损失函数上differentiable loss。在本章节我们公式化的表示形如公式（2）的损失函数L。他有两部分组成：惩罚外貌上的差异penalizes differences in appearance，惩罚ϕ局部空间变化。在本实验中是和F之间的负局部相关性negative local cross-correlation。这是一个常用的度量，对扫描和数据集之间经常发现的强度变化有鲁棒性。

       让和表示减去局部均值的图像，我们计算局部均值在一个体volume，在本文的实验中n=9 。F和的局部互相关为：

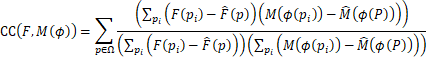(5)

pi在p的体邻域volume上迭代。CC值越大表示对其效果也好，相对损失函数而言：

，CC的高效计算仅使用F和上的卷积操作。

       最小化的会让更加接近F，但是也许会生成一个不连续discontinuous的形变场ϕ。因此使用在ϕ空间梯度spatial gradient上一个扩散约束diffusion regularizer来平滑形变场ϕ：

(6)

我们利用相邻体素之间的差异来近似空间梯度spatial gradient。

(7)

λ是正则化参数regularization parameter。

五、实验

5.1数据集

       标准的预处理包含仿射空间归一化affine spatial normalization，提取extraction，和裁剪crop。最好能够进行解刨学分割。质量控制quality control(QC)是人工检测的分割误差。

       Atlas-based代表一个参考，要么是平均体average volume，要么是联合和反复对齐大脑数据集来构建并将它们平均起来的。

5.3 Dice Score

       为这些数据获取密集的真是配准并不是很准确，因为很多的配准域也会有相同的结果。本文的评估手段是使用解刨学分割。和 分别表示和F的结构k。

（8）

5.4 实施

通过Tensorflow后端的Keras实施，我们使用学习率为ADAM optimizer。为了减少内存的使用，每个训练批次batch由一对体组成volumes。使用不同的λ独立训练不同的网络。最优化Dice Score作为验证数据。