CRC校验
https://blog.csdn.net/li200503028/article/details/26591243 参考这个
https://wenku.baidu.com/view/ba00e904bed5b9f3f90f1c1b.html 这个极好
http://blog.163.com/fpga_ip/blog/static/2044430242012558747194/
原理参考这个:http://blog.51cto.com/winda/1063951
- CRC校验码的计算示例
由以上分析可知,既然除数是随机,或者按标准选定的,所以CRC校验的关键是如何求出余数,也就是校验码(CRC校验码)。
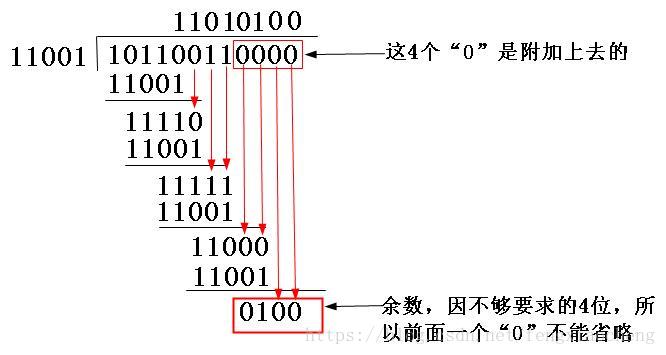
下面以一个例子来具体说明整个过程。现假设选择的CRC生成多项式为G(X) = X4 + X3 + 1,要求出二进制序列10110011的CRC校验码。下面是具体的计算过程:
(1)首先把生成多项式转换成二进制数,由G(X) = X4 + X3 + 1可以知道(,它一共是5位(总位数等于最高位的幂次加1,即4+1=5),然后根据多项式各项的含义(多项式只列出二进制值为1的位,也就是这个二进制的第4位、第3位、第0位的二进制均为1,其它位均为0)很快就可得到它的二进制比特串为11001。
(2)因为生成多项式的位数为5,根据前面的介绍,得知CRC校验码的位数为4(校验码的位数比生成多项式的位数少1)。因为原数据帧10110011,在它后面再加4个0,得到101100110000,然后把这个数以“模2除法”方式(就是异或)除以生成多项式,得到的余数(即CRC码)为0100,如图5-10所示。注意参考前面介绍的“模2除法”运算法则。
图5-10 CRC校验码计算示例 首位为1进行异或,为0直接移位处理就可以,下面就有的直接移位的两位
(3)把上步计算得到的CRC校验0100替换原始帧101100110000后面的四个“0”,得到新帧101100110100。再把这个新帧发送到接收端。
(4)当以上新帧到达接收端后,接收端会把这个新帧再用上面选定的除数11001以“模2除法”方式去除,验证余数是否为0,如果为0,则证明该帧数据在传输过程中没有出现差错,否则出现了差错。
循环冗余校验码(CRC)的基本原理是:
将被处理的报文比特序列当做一个二进制多项式A(x)的系数,(任意一个由二进制位串组成的代码都可以和一个系数仅为‘0’和‘1’取值的多项式一一对应。例如:代码1010111对应的多项式为x6+x4+x2+x+1,而多项式为x5+x3+x2+x+1对应的代码101111),该系数乘以2^n(n为生成多项式g(x)中x的最高次幂)以后再除以发送方和接收方事先约定好的生成多项式g(x)后,求得的余数P(x)就是CRC校验码,把它副到原始的报文A(x)后面形成新的报文即为A(x)*x^n+P(x),并且发送到接收端,接收端从整个报文中提取出报文B(x)(即为发送端的A(x),此时不能保证发送正确所以用B(x)表示),然后用与接收端同样的做法将B(x)对应的二进制序列乘以2^n(左移n位)后,除以事先约定好的g(x)得到一个余数p(x),此时如果接收报文中的CRC校验码与计算得到的校验码相同,即P(x)=p(x),则传输正确,否则传输有误,重新传输。
上述工作过程中有几点需要注意:
1.在进行CRC计算时,采用二进制(模2)运算法,即加法不进位,减法不借位,其本质就是两个操作数进行逻辑异或运算;
2.在进行CRC计算前先将发送报文所表示的多项式A(x)乘以x“,其中n为生成多项式p(x)的最高幂值。对二进制乘法来讲,A(x)·x“就是将A(x)左移n 位,用来存放余数p(x),所以实际发送的报文就变为A(x)·x^n+p(x):
3.生成多项式g(x)的首位和最后一位的系数必须为1,且生成多项式根据不同国家的标准有不同的形式。
CRC校验码检错的原理如下图
![]()
(以上关于CRC校验的介绍来自硕士论文《基于FPGA的串行通信实现与CRC校验》加上本人的理解做了一些改动)
下面举例说明CRC校验码的求法:(此例子摘自百度百科:CRC校验码)
信息字段代码为: 1011001;对应m(x)=x6+x4+x3+1
假设生成多项式为:g(x)=x4+x3+1;则对应g(x)的代码为: 11001
x4m(x)=x10+x8+x7+x4 对应的代码记为:10110010000;
采用多项式除法: 得余数为: 1010 (即CRC校验字段为:1010)
发送方:发出的传输字段为: 1 0 1 1 0 0 1 1010
给出余数(1010)的计算步骤:
除法没有数学上的含义,而是采用计算机的模二除法,即,除数和被除数做异或运算。进行异或运算时除数和被除数最高位对齐,按位异或。
10110010000
^11001
--------------------------
01111010000
1111010000
^11001
-------------------------
0011110000
11110000
^11001
--------------------------
00111000
111000
^11001
-------------------
001010
则四位CRC校验码就为:1010。
利用CRC进行检错的过程可简单描述为:在发送端根据要传送的k位二进制码序列,以一定的规则产生一个校验用的r位监督码(CRC码),附在原始信息后边,构成一个新的二进制码序列数共k+r位,然后发送出去。在接收端,根据信息码和CRC码之间所遵循的规则进行检验,以确定传送中是否出错。这个规则,在差错控制理论中称为“生成多项式”。
下面给出CRC校验码的verilog实现方式:
本例中实现了求得8bit信息序列的CRC校验码,生成多项式取g(x)=X^16+X^12+X^5+1,对应的生成序列为1_0001_0000_0010_0001,输入的8bit序列data左移16位后得到stemp={data,16‘b0000_0000_0000_0000} ,每次异步复位信号rst_n复位时将crc的值清零并把线型变量stemp的值打入寄存器temp中,然后通过时序电路将temp与生成多项式对应的序列进行多次按位异或,最终得到一个小于生成序列的temp后,temp[15:0]的值即为CRC校验序列,并把它赋给输出crc。
下面是code:
module crc(clk,data,rst_n,crc );
input [7:0] data;
input clk;
input rst_n;
output reg [15:0]crc=0;
wire[23:0]stemp;
reg[23:0]temp=0;
parameter polynomial=17'b1_0001_0000_0010_0001;
assign stemp={data,16'b0000000000000000};
always @ (posedge clk or negedge rst_n)
begin
if(!rst_n)
begin
crc<=0;
temp<=stemp;
end
else
begin
if(temp[23]) temp[23:7]<=temp[23:7]^polynomial;
else if(temp[22]) temp[22:6]<=temp[22:6]^polynomial;
else if(temp[21]) temp[21:5]<=temp[21:5]^polynomial;
else if(temp[20]) temp[20:4]<=temp[20:4]^polynomial;
else if(temp[19]) temp[19:3]<=temp[19:3]^polynomial;
else if(temp[18]) temp[18:2]<=temp[18:2]^polynomial;
else if(temp[17]) temp[17:1]<=temp[17:1]^polynomial;
else if(temp[16]) temp[16:0]<=temp[16:0]^polynomial;
else crc<=temp[15:0];
end
end
endmodule