【分层图】【BOI2007】Fence
题目描述
Leopold is indeed a lucky fellow. He just won a huge estate in the lottery. The estate contains several grand buildings in addition to the main mansion, in which he intends to live from now on.However, the estate lacks a fence protecting the premises from trespassers, which concerns Leopold to a great extent. He wants to build a fence and, in order to save money, he decides it is sufficient to have a fence that encloses the main mansion, except for one important restriction: the fence must not lie too close to any of the buildings. To be precise, seen from above, each building is enclosed in a surrounding forbidden rectangle within which no part of the fence may lie. The rectangles’ sides are parallel to the x- and y-axis. Each part of the fence must also be parallel either to the x-axis or the y-axis.
Help Leopold to compute the minimum length of any allowed fence enclosing the main mansion.
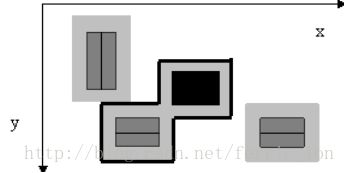
Figure 1: The main mansion (black) and three other buildings with surrounding forbidden rectangles. The thick black line shows a shortest allowed fence enclosing the main mansion.
输入
The input is read from a text file named fence.in. The first line of the input file contains a positive integer m(1≤m≤100) , the number of buildings of the estate. Then follow m lines each describing a forbidden rectangle enclosing a building. Each row contains four space-separated integers tx , ty , bx , and by , where (tx,ty) are the coordinates of the upper left corner and (bx,by) the coordinatesof the bottom right corner of the rectangle. All coordinates obey 0≤tx<bx≤10,000 and 0≤ty<by≤10,000 . The first rectangle is the forbidden rectangle enclosing the main mansion.
输出
The output is written into a text file named fence.out. It contains one line with a single positive integer equal to the minimum length of any allowed fence enclosing the main mansion.
样例输入
4 8 4 13 8 2 1 6 7 4 7 9 11 14 7 19 11
样例输出
32
为什么要在2016年的最后一天写这道题。
第一眼看到:好像就是个矩形判交并查集一下做周长并吧。
数据范围 100 好像暴力就行。
写写写感觉不对。最短的栅栏,不一定全贴上啊。
那就是扫描线,每次找左端点和右端点,转移一下就行。
写写写写完了,样例调一会儿出来了。闭目沉思了一下,立马发现了一个范例:一个棒状物体插入凹陷中,因为栅栏不能穿过所以很显然不能直接取两个端点。
这什么题啊我的妈。老师把这题放在分层图专项于是找了一下论文。果然玄学做法啊。搜了一下BOI2007的网站居然还能上。于是搞到了数据题解和标程。看了一下当年的情况,最高分25。
……
老师:“我也不知道这题啥难度就放上去了。”
……
说一下我的理解吧。这题一开始看到真的不容易想到转化成最短路。
可以枚举每个矩形的每个顶点,如果两个顶点都不在某个矩形内部,且两个顶点之间形成的区域(矩形或者一条线,这个地方没看懂论文(中文/英文写的一样)坑了半天),说明可以建一条栅栏(横和竖),所以可以在这两个顶点之间连一条权值为曼哈顿距离的边,表示可以建合法的栅栏。因为矩形只有 100 ,顶点最多 400 ,可以暴力枚举加边。连上一堆边后,问题转化为找包含主建筑的最小回路。如何判断回路包含某个点呢?可以用射线法,即从点任意引出一条射线,与多边形交奇数个点则在多边形内,否则在多边形外。(这里也纠结了很久,因为跟线段交于端点不好处理)发现标程只是从主建筑左上角引出一条向上的射线,就照着抄了。但是怎么表示交点的奇偶性呢?这里就用到分层图的思想了。 dist[i][0] 表示与当前路径交偶数个点, dist[i][1] 表示与当前路径交奇数个点。当某条路径与射线相交时,会发生图层的改变。所求回路就是从 [i][0] 开始,到 [i][1] 的最短路。因为点数只有 400 ,可以暴力对每个点做最短路。
这题一上午才看懂题解看懂标程判两个点之间无覆盖的方式,下午写了一会wa了。最近做图专项,USACO卡spfa卡的有点狠就写了堆优dijkstra。调了半天,硬对了的建出来的边建出来的点,都没错那就是dijkstra写错了。也没错,一天就这么郁闷的过去了。
晚上回家一看:
struct rec{
int to, lay, len;
bool operator<(const rec &x)const{
return to>x.to;
}
}我还能说点啥。
郁闷的2016,希望2017会好。
代码:
#include 110];
struct edge{
int to, lay, len;
edge *next;
edge(int t, int la, int le, edge *n):to(t), lay(la), len(le), next(n){}
}*g[410][2];
struct dot{
int x, y;
dot(){}
dot(int X, int Y):x(X), y(Y){}
bool operator<(const dot &a)const{
return x==a.x?y410];
struct rec{
int to, lay, val;
rec(int t, int l, int v):to(t), lay(l), val(v){}
rec(){}
bool operator<(const rec &x)const{
return val>x.val;//哭
}
};
int n, h, ans, dist[410][2];
priority_queue Q;
//判断点是否在任意一个矩形内
bool in(dot a){
for(int i=0;iif(a.x>s[i].x1&&a.xs[i].y1&&a.yreturn true;
return false;
}
inline int ABS(int a){return a<0?-a:a;}
//加边,p为1表示与射线有交点,需要换层
void addedge(int a, int b, bool p, int l){
if(!p)
g[a][0]=new edge(b, 0, l, g[a][0]), g[a][1]=new edge(b, 1, l, g[a][1]),
g[b][0]=new edge(a, 0, l, g[b][0]), g[b][1]=new edge(a, 1, l, g[b][1]);
else
g[a][0]=new edge(b, 1, l, g[a][0]), g[a][1]=new edge(b, 0, l, g[a][1]),
g[b][0]=new edge(a, 1, l, g[b][0]), g[b][1]=new edge(a, 0, l, g[b][1]);
}
void dijkstra(){
ans=0x3f3f3f3f;
for(int i=0;imemset(dist, 0x3f, sizeof dist);
while(!Q.empty()) Q.pop();
Q.push(rec(i, 0, 0)); dist[i][0]=0;
rec w;
while(!Q.empty()){
w=Q.top(); Q.pop();
if(w.val>=ans)
break;
if(w.to==i&&w.lay==1){
ans=w.val;
break;
}
if(w.val>dist[w.to][w.lay])
continue;
for(edge *t=g[w.to][w.lay];t;t=t->next)
if(dist[t->to][t->lay]>dist[w.to][w.lay]+t->len){
dist[t->to][t->lay]=dist[w.to][w.lay]+t->len;
Q.push(rec(t->to, t->lay, dist[t->to][t->lay]));
}
}
}
}
int main(){
scanf("%d", &n);
for(int i=0;iscanf("%d%d%d%d", &s[i].x1, &s[i].y1, &s[i].x2, &s[i].y2);
//记录主建筑矩形左上角的点
int X=s[0].x1, Y=s[0].y1;
//找到可行的点
for(int i=0;iif(!in(dot(s[i].x1, s[i].y1)))
arr[h++]=dot(s[i].x1, s[i].y1);
if(!in(dot(s[i].x2, s[i].y1)))
arr[h++]=dot(s[i].x2, s[i].y1);
if(!in(dot(s[i].x1, s[i].y2)))
arr[h++]=dot(s[i].x1, s[i].y2);
if(!in(dot(s[i].x2, s[i].y2)))
arr[h++]=dot(s[i].x2, s[i].y2);
}
//按x坐标排序方便后续处理
sort(arr, arr+h);
sort(s, s+n);
for(int i=0;i//mi:可行区域上边界 ma:可行区域下边界
int k=0, mi=0, ma=10000;
while(k//点的横座标在s[k]的x范围内s[k]才会产生影响
if(s[k].x2>arr[i].x){
if(s[k].y1>=arr[i].y)
ma=min(ma, s[k].y1);
else if(s[k].y2<=arr[i].y)
mi=max(mi, s[k].y2);
}
k++;
}
for(int j=i+1;j//i和j之间的部分
while(kif(s[k].y1arr[i].y)
mi=s[k].y2, ma=s[k].y1;//其实已经不合法了
//仍然对i处理
else if(s[k].y1>=arr[i].y)
ma=min(ma, s[k].y1);
else if(s[k].y2<=arr[i].y)
mi=max(mi, s[k].y2);
k++;
}
//不合法的点对
if(mabreak;
if(arr[j].y>=mi&&arr[j].y<=ma){
int len=ABS(arr[i].x-arr[j].x)+ABS(arr[i].y-arr[j].y);
if(arr[i].x<=X&&arr[j].x>X&&arr[i].y<=Y&&arr[j].y<=Y)
addedge(i, j, 1, len);
else
addedge(i, j, 0, len);
}
}
}
dijkstra();
printf("%d\n", ans);
return 0;
} 坠短路真神奇啊……分层图更神奇啊……
好久不更带代码的博客感觉代码风格变了不少……
2017RP++。