省选之路

其实是一个咕了很多东西的blog

动态规划-Undone

线性DP

树形DP

状压DP

数位DP

概率DP

树

堆 - heap

这个专题主要掌握二叉堆和左偏树。一般二叉堆可以满足很多题目要求，仅当需要合并的时候才使用左偏树。

AC自动机 - AC automaton

Goal 这个专题主要掌握普通的Hash(或stl::map)，KMP算法与AC自动机。AC自动机是一个很多变的数据结构，本质是Trie，但是可以根据fail数组和next数组将其转化成一张图。重点是弄懂其fail数组与next数组的工作原理，于是图加上完整的边后就能与DP（注意若状态转移长度只能保留其后缀长度），矩阵快速幂（dijkstra的思想），图论（强连通分量），概率（掷骰子出现某个数字串的概率）。

Hint 出现多个字符串就可以往AC自动机上套。

others BM算法(后缀匹配)，扩展KMP算法(任意后缀的前缀数组)，RK算法(基于字符串Hash),manacher算法(回文字符串匹配)

最近公共祖先 & 区间极值 - LCA & RMQ

Goal 知道LCA转RMQ==（欧拉序），知道ST表与ST树（线段树）==的应用。

RMQ的两种实现方法：ST树（重修改）和ST表（重查询）。

LCA的两种实现方法：寻找最深公共根路径节点（对应倍增与并查集，重单次查询多次修改）和寻找最浅最短路径节点（对应Tarjan算法，重多次查询）。

线段树 & 树状数组

维护一段区间内的DP值。

线段树的应用，注意基本操作之间的差异。

• 拆分与合并信息。新增维护的量，考虑边界与否。

• 一般来说虽然线段树常数大，但是用来处理修改和查询的结合的题目比较直观。

• RMQ问题只能用线段树。

树状数组的应用，注意下标与键值的意义。

• 可以用于查询第k小和逆序对。

• 树状数组更容易提高维度。

树链剖分

重链剖分：选取子树最大的节点作为重链，维护DFS序使其链上节点序号连续，且子树序号亦连续。用线段树维护子树与区间修查。

平衡树

技巧：splay和treap都是灵活性高的数据结构，可以根据题意来设置操作。

treap

• split有两种，按照节点键值和子树大小。
• merge可以直接返回L或R（方便些），也可以传引用。
• delete注意只删一个，而无旋treap不支持count，所以把v都提出来，去掉一个，再合并。
• rotate传参一般传引用，多画图。
  查询rank，K-th，pre，sur注意边界，键值等于v的点在哪个子树。
• reverse推标记，把左右儿子换一下就行。
• pushdown操作在所有要改变树形态的操作前，pushup在之后。

splay

• splay一般是(x,y)，将x移到y的下方，也有直接移到root。

• rotate更新关系注意gfa存在与否，这一点在LCT里很重要。

• ins & del这个就可以count了。记得ins后要splay。

• pre & sursplay到根，然后while到底。

• reverse 转到左子树的右子树，打标记。

分治

点分治是处理树上有权路径问题的算法。

点分治和树形DP？其实点分治一部分可以转化为树形DP，点分治重找重心本身也是树形DP。

主要流程（递归）：找重心 > 处理子树节点 > 对子树根节点进行计算 > 根据容斥原理删去子树答案 & 找重心

动态树 - LCT

LCT是以Splay 为实现基础的，本质是森林，但splay跟平常的不一样，pushdown操作也需要注意，即关于reverse的处理。

其中涉及两个点操作的都需要$access+splay$。

尤其要注意实边和虚边的处理。还是不太懂

基本操作很多，但是理解为主，代码量很小。

数据结构技巧

图

图的生成树

最短路算法（单元/多元）

1. Floyd：利用动态规划($DynamicProgramming$)进行设计，经常利用k层循环的本质出题。
2. Dijkstra：利用贪心算法($GreedyAlgorithm$)进行设计，每次选出距离起点最近的点进行Relax，因为只顾及已知距离，无法处理负边权。
3. SPFA：利用动态规划($DynamicProgramming$)进行设计，将队列里的节点进行Relax，并将短于最佳答案的入队。如果存在负环，则一定有环上的点被Relax两次。求最长路，可以将边权取负。
4. Johnson：将负边权变成正的，然后根据公式进行n次Dijkstra。Dijkstra的推广算法。

最小生成树

​ 最小权重生成树的简称，使所有边权和最小。

1. Prim：类似Dij的贪心的Relax方式。感觉用处不大。
2. Kruskal：贪心选择边权小的边，用并查集维护两点是否连通。

• $Ex\alpha$：增量最小生成树：每加入一条有权边输出当前一次最小生成树。根据回路的性质，只需删除新环中权值最大的边。

• $Ex\beta$：次小生成树：同上，枚举新环，得到一个删除后使得权值和之差最小。

• $Ex\gamma$：最小生成树计数：生成最小生成树，得到每种权值的边使用的数量x，然后对于每一种权值的边搜索，得出每一种权值的边选择方案，然后乘法原理。

• $Ex\delta$最小瓶颈路径：使路上最大边权最小。用Kruskal生成最小瓶颈生成树，树上任意路径$E(u,v)$都是$(u,v)$的最小瓶颈路径。

• $Exϵ$：最舒适路径：是路上最大边权$-$路上最小边权最小。

  逆向思维：枚举最小边，尺取法，二分答案。并查集维护连通性。

• $Ex\zeta$：多次询问$(u,v)$最大瓶颈路上的最小边权。

  即在最大瓶颈树上寻找最小边，使用倍增LCA。

• $Ex\eta$：最小乘积生成树：Undone

• $Ex\theta$：To be continue$\Rightarrow$

拓扑序

​ 拓扑排序后任意点满足连向其的点在其前，其连向的点在其后。

​ 这样有利于DP转移，是DAG-DP的基本顺序，也可以判环，求割点，其实都是维护点转移的顺序。

• $Ex\alpha$：拓扑序不唯一，但是求字典序最小的拓扑序列的时候，可以考虑从出度倒推。

欧拉回路

​ 从任意点出发，每条边只经过一次回到该点，则我们称这张图存在欧拉回路。（一笔画问题）

​ 充要条件：无向图任意点的所有度数为偶数，有向图任意点的入度和出度相同。

差分约束

​ 给出形如$x-y<=b$的不等式，求问题的解。转化为$(y,x)=b$，然后跑最短路，无解说明有负环，应该考虑算法。通过代数问题转化为差分约束。

K短路

​ 由最短路的扩展我们知道一个点入队多少次，就得到第几短的路径。设计一个A*进行Spfa。估价函数：反向边跑终点单源最短路。

2-SAT的匹配

​ 引入交替路和增广路的概念。匈牙利算法即不断寻找增广路来更新交替路的过程。有点像网络流。不太懂。

最小环的计算-Undone

图的连通性

强连通分量

tarjan

​ 可以生成一颗dfs/bfs树，并且很有性质。以下四个定义皆使用此树解。

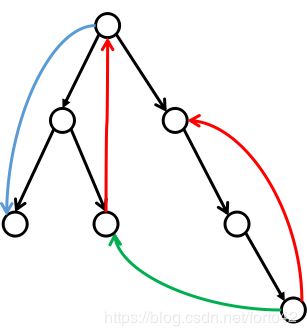
​ 如图，黑色为树边，蓝色为前向边，红色为返祖边，绿色为横叉边。

kosaraju

​ 是根据强连通分量独特性质：顺逆皆可到达分量内任意一点，用图和反图来设计的算法。

以下定义仅针对无向图。

割点

​ 感性理解即去掉后连通块数量增加。可根据拓扑序结合乘法原理来判断。是否有边跨过是唯一判断标准，那么只要有一个孩子满足dfn[u]<=low[v]即可。

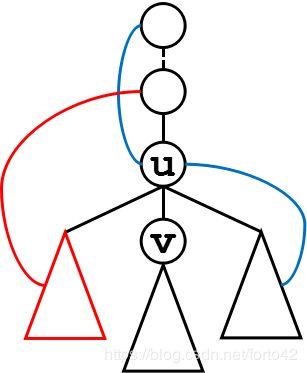
桥

​ 即割边。定义同理。比点简单，如果E(u,v)满足dfn[u]

双连通分量

​ 删除点或边仍连通的图或分量称为对应的双连通分量。没有横叉边，前向边与返祖边统称跨越边。

双点连通分量

​ 利用栈。儿子满足没有跨越边的子树即为一个点双，包括自己在内。

双边连通分量

​ 删除割边，其他都是边双连通分量。

二分图-Undone

2-SAT

最大匹配——匈牙利算法

网络流

推荐博客

最大流与最小费用最大流

​ 最大流与最小费用最大流，是网络流最基础的两种模型。

FF

​ 单路增广。DFS寻找一条路径并记录前驱，找到路径后再回溯处理边权。$O(V{E}^2)$

EK

​ 单路增广。每次使用BFS寻找一条路径并记录前驱，找到路径后再回溯处理边权。$O(V{E}^2)$

Dinic

​ 多路增广。预处理优化访问次数。每次计算多条路径，并同时处理边流，减少了运行次数。$O(V^{2}E)$

SAP

​ 没用过。据说Gap优化后飞起。

​ 求最小费用最大流时使用Spfa保证是最短路径。

​ Q 为什么会有最小费用最大流？

​ 1️⃣当一个图有很多路径供选择的时候，自然会产生更优的路径阶级分化。

​ 2️⃣当一个图需要求最短路并且有后效性的时候，最短路或DP不适用。

最大流及其变式

​ 最大流，最小割，最小覆盖集，最大独立集等。由二分图引入，均可使用最大流的模型求解。

有上下界的网络流

推荐博客

入题

​ ▶️ 提取题目信息。

​ 点：题目描述的对象，平面图中的点，时间点段等。

​ 边：对象之间的关系，平面图中的边，时间推移等。

​ ▶️ 思考一条路径的意义。

​ 判断是否可以建模。如最大流使得一条路径为所求，最小割则不可以存在路径连通S-T，等等，按照题目抽象出来的本质思考。有了路径，就可以很快确定点和边的含义。

解题

拆点

​ ⬛️ 将入度和出度独立处理，通常和floyd一起使用。

​ ⬛️ 限流，即每个点经过的次数​。点的限制转化为边的限制。

​ ⬛️ 时间推移导致点信息的变化和转移。

边

​ 主要是设计边的流量和费用。一些非常规操作：

​ 1. 点的经过次数（次数即流量）。

​ 2. 流量为inf保证不参与决策，仅起到连接作用。

其他

​ ⚫️ 二分答案，在跑到给定流的情况下求限制值的极值。

​ ⚫️ 无序化有，定义序关系以适应网络流模型中的有向边。

​ ⚫️ 零一点集，源集汇集则分别为01点集，源集内的点即为选择的点。

​ ⚫️ 满流问题，入度=出度，应用于欧拉判环或者平衡问题。

数论

矩阵相关

矩阵运算

普通运算一次为$O(N^3)$的复杂度，$C[i][j]={\Sigma }_{i=1}^{n}a[i][k]\times b[k][j]$。可优化至$O(NlogN)$。

快速幂

最常见的用法是优化线性递推，还可以运用到闭合回路中k条边的方案数，AC自动机DP（传递闭包）中优化递推。

高斯消元

解n元1次方程组。矩阵求逆。

数学公式

素数判定

直接枚举到$\sqrt{N}$判断因数。

Miller-Robin算法（随机算法）-Undone

欧拉函数

表示$[1,n)$ 中与 n 互质的数的个数:$\phi (n)={\Sigma }_{i=1}^n(gcd(i,n)==1)=n(1-\frac{1}{p_1})(1-\frac{1}{p_1})\dots (1-\frac{1}{p_n}),p_i|n$

线性筛

对于每一个质数 x，筛去所有 x 的倍数。每次用这个数乘上质数去筛，当最小的某质数为该数因子的时候结束。

for(int i = 1; i <= sqrt(n); ++i) {
	if(!isPrime[i]) prime[++prime_cnt] = i;
	for(int j = 1;j <= prime_cnt && i * prime[j] <= n;++j) {
		isPrime[i*prime[j]] = 1;
		if(i%prime[j]==0) break;
	}
}

线性筛与函数递推

• 最小质因子：

min_divisor[i * prime[j]] = prime[j];

• 欧拉函数：

phi[1] = 0;
if(!isPrime[i]) phi[i] = i - 1;
if(i % prime[j]) phi[i * prime[j]] = phi[i] * phi[prime[j]];
else {phi[i * prime[j]] = phi[i] * prime[j]; break;}

• To be continued$\to$

gcd & exgcd

辗转相除法。exgcd是求$ax+by=c(gcd(a,b)|c)$ 的解集 $(x,y)$，可以用来求逆元。

$s(k)={\Sigma }_{i=1}^n(gcd(i,n)==k)=\phi (n/k)$。

逆元

$a\%m/b\%m\ne a/b\%m$，因此需要求$b^{-1}$即b的逆元，使得$a\%m\ast b^{-1}\%m=a/b\%m$。就是在模数意义下去掉除法运算。

特别地，当模数为质数的时候，一个数的逆元就是该数的模数减二次幂。

线性求逆元:$i^{-1}\equiv -\lfloor \frac{p}{i}\rfloor \ast (p\%i{)}^{-1}(modp)$ 代码:$inv[i]=(p-\frac{p}{i})\ast inv[p\%i]\%p;$

莫比乌斯反演-Undone

CRT-Undone

排列组合

记住，排列是考虑顺序的，数与数之间有差别。
排列通用公式：$A_n^m=\frac{n!}{(n-m)!}$。
这个很容易理解，第$i$个位置上面有$n-i$中选择，乘法原理。
而考虑排列时，总是先考虑未编号的方案。
有重复元素的全排列：有$n$种元素，第$i$种有$n_i$个，设$n=\Sigma n_i$，则$A=\frac{n!}{\Sigma n_i!}$。

组合通用公式：$C_n^m=\frac{n!}{m!(n-m)!}$。即去掉全排列的方案数。
可重复选择的组合：$C_{n+km-1}^m$。设第$i$个元素选$x_i$个，则$k=\Sigma x_i$，设$y_i=x_i+1$，则$n+k=\Sigma y_i$。隔板法：相当于在$n+k$个元素中插入n-1个隔板，方案数为$C_{n+k-1}^{n-1}=C_{n+k-1}^k$。

${\Sigma }_{r=1}^{n}r\cdot C_n^r=n\cdot 2^{n-1}$
${\Sigma }_{k=0}^m{C}_{n+k}^n=C_{n+m+1}^m$
${\Sigma }_{r=0}^n{C}_n^r=2^r$
${\Sigma }_{r=0}^n{2}^r\cdot C_n^r=3^r$

组合数学八题——球盒问题

序号	n球	m盒	允许不放	方案数
A	异	异	T	$m^n$
B	异	异	F	$f{(}_m^n)=m\times f({(}_{m-1}^{n-1})+{(}_m^{n-1}))$
C	异	同	T	${\Sigma }_{i=1}^{m}f{(}_i^n)$,转移同下
D	异	同	F	$f{(}_m^n)=f{(}_{m-1}^{n-1})+m\times f{(}_m^{n-1})$
E	同	异	T	$C_{n+m-1}^{m-1}$
F	同	异	F	$C_{n-1}^{m-1}$
G	同	同	T	$g{(}_m^n)=g{(}_{m-1}^n)+g{(}_m^{n-m})$
H	同	同	F	$g{(}_m^{n-m})$

简要证明：
A 球放到每个盒子都是独立的，所以每个球有m种选择。
B-D 先考虑D，转移两种方式：放和不放新盒子，不放有m种选择。C可以不放，相当于挑i个盒子放的方案数总和。B则是放新盒子有m种情况。
E-F 插板法。
G-H 不是很会

Lucas&exLucas-Undone

当组合数需要模一个质数时。$C(n,m)\%p=C(n/p,m/p)\ast C(n\%p,m\%p)\%p;C(n,0)=1$

CATALAN数-Undone

$h(n)=\Sigma h(i)\cdot h(n-i-1)$
$h(n)=\frac{C_{2n}^n}{n+1}$

STIRLING数&STIRLING反演-Undone

将n个数分成m个集合的方案数$S(n,m)$。

广义容斥（二项式反演）-Undone

置换与循环节-Undone

生成函数-Undone