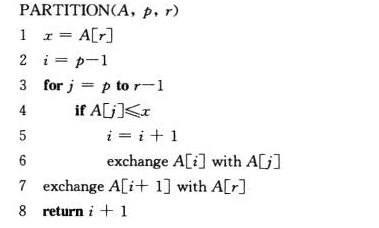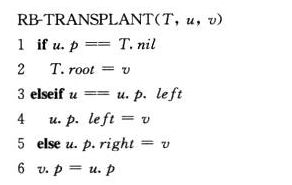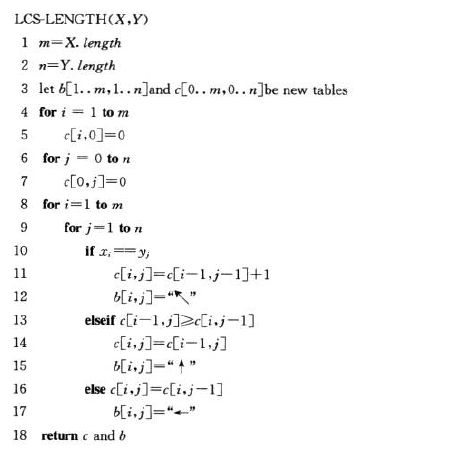注意点:
- 通俗的讲的时候,就是个人的理解了,仅作参考。
- 作为一个Java程序员,有必要了解算法,如果有成为一个优秀程序员的想法,算法和数据结构只是基础。当然对于非CS专业,计算机网络,操作系统,编译原理等也是后面需要补充的基础知识点。
- 关于阅读《算法导论》的一些建议:
不必纠结于数学的证明,例如递归表达式的时间复杂度计算;把一些当前重要的知识点(比如从第一部分到动态规划、贪心算法,高级数据结构B树那里)先看了,完成从0到1的过程,本文也将记录到那里。- 好记性不如烂笔头,冥思苦想不如画个图...人的记忆力是有限的,关于计算机的知识点是很多的,把重要的记录下来,以后忘了,回过头再看看,由于你记录的是要点,所以不必再次翻看一遍全书,即可很快的复习一遍。
- 看书不必非得按照顺序来看,连JMM都知道,除非两个步骤都有依赖关系,否则可以乱序执行,称为重排序
- Good luck to everyone who wants to be a not-so-bad programmer.
关于几个时间复杂度
通常情况下,当数据量足够大时,一般满足
θ(1)>θ(N)>θ(NlogN)>θ(N^2) (>代表优于)
1.算法基础
1.1 插入排序
时间复杂度:O(N^2)
思想:每次从右至左跟已排序数列进行对比,放入合适位置。两次遍历,一次相当于摸牌,另一次相当于具体的查找算法。
1.2 分治法
将问题分解为几个规模较小但类似于原问题的子问题,递归的求解这些子问题,然后再合并这些子问题的解来建立原问题的解。(分解-解决-合并)
归并排序
时间复杂度O(NlogN)(O还是θ——theta,都差不多)
归并排序算法如下:
函数的增长
O渐进上界Ω渐进下界,o和ω
具体看数学定义最清楚。
分治策略
求解递归式的三种方法:
- 代入法:靠猜测,一般人不是很靠谱,需要较强的数学功底
- 递归树法:
-
主方法
可求解形如
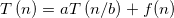
的函数。
最大子序列问题
思路简单,分成两个子序列,最大和要么全在左侧序列,要么全在右侧序列,要么跨中点;简单写法的参考简单版本,但是有个点需要注意一下,代码给出的复杂度是O(N)
2. 排序
如果输入数组中仅有常数个元素需要在排序过程中存储在数组之外,则程排序算法是原址的(in place)。例如,排序算法中的swap操作。
顺序统计量:一个n个数的集合的第i个顺序统计量就是集合中第i小的数。
2.1 堆排序
堆排序的时间复杂度是O(NlgN),具有空间原址性。
堆
二叉堆是一个数组,它可以被看成是一个近似的完全二叉树(按层序排列,各个节点的序号同满二叉树相同)
二叉堆可以分为两种形式:最大堆和最小堆(最大还是最小取决于对应的二叉树的所有双亲节点是否都大于或小于其孩子节点的值)。堆排序算法中,使用的是最大堆。最小对通常用于构造优先队列。
排序
-
维护堆的性质
通俗的讲,就是保持数组的最大堆性质。思路比较简单,比较parent节点和孩子节点,找到最大值,如果最大值是某个孩子节点,交换,递归运行。对于树高为h的节点来说,该程序时间复杂度为O(h)
-
建堆
建堆过程,说白了就是对每一个非叶节点进行(1)的操作。复杂度O(n)
-
堆排序算法
交换A[1]和A[n],此时最大的数已经位于最后一个位置。然后调整剩下的n-1个数据,调用(1)的方法;再交换A[1]和A[n-1],如此下去。复杂度O(lgn)
具体堆排序过程可参考图解堆排序(不过也注意,其中有一些问题,哪些节点有子节点,从1开始标,应该是(n/2)向下取整)
堆的应用——优先队列
优先队列(priority queue)是一种用来维护由一组元素构成的集合S的数据结构,其中的每一个元素都有一个相关的值,称为关键字(key)
最大优先队列应用:例如在共享计算机系统的作业调度。
最小优先队列应用:用于基于事件驱动的模拟器。
2.2 快排
最坏情况复杂度θ(n^2),元素互异的情况下期望时间复杂度θ(NlgN),通常是实际排序应用中最好的选择。
思路(采用分治策略)
- 数组A[p..r]划分为两个子数组A[p..q-1]和A[q+1..r],st.∀ x∈A[p..q-1],y∈A[q+1..r]都有x≤A[q]≤y
- 递归调用,对子数组进行排序。
-
由于是in place排序,所以不需要合并操作。
伪代码:
数组的划分
数组划分一点分析:默认以A[r]——最后一个元素作为比较中间点,for循环遍历A数组,j指向每个被遍历元素下标;i指向小于A[r]的下标。
画个图理解一下最清楚了:
算导叫法,A[r]称为主元(pivot element)
性能分析
最坏情况:划分产生子问题元素个数为n-1和0时。此时,T(n)=θ(n2)。当输入数组完全有序时,快排复杂度为θ(n2),插排只有O(n)
最好情况:划分得到的两个子问题的规模都不大于n/2.复杂度θ(nlgn)
快排随机化版本
这个思路简单,随机选取主元,与A[r]交换,再利用上面的算法计算即可。此种版本主要解决,近乎有序的情况带来的原有快排最坏情况的发生。
2.2 线性时间排序
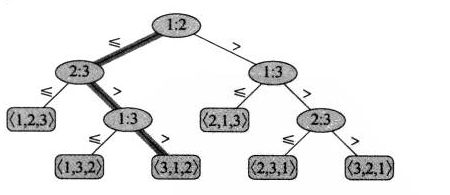
在排序的最终结果中,各元素的次序依赖于它们之间的比较,这类排序算法称为比较排序。
三种线性时间复杂度的排序算法:计数排序、基数排序和桶排序。
比较算法采取决策树模型:这里的内部节点用i:j的形式代表A[i]和A[j]进行比较。≤则进左子树比较,反之右子树进行比较。叶子节点给出了最后的顺序。
计数排序
数据结构
支持插入删除操作的动态集合称为字典。
栈和队列
栈(stack),后进先出,LIFO
插入称为压入(push),删除称为弹出(pop)。可以简单的理解为有底无盖的杯子。
队列(queue)插入称为入队(enqueue),删除称为出队(dequeue)
链表:
单链表、双向链表、循环链表,建议看下《大话数据结构》了解一下就可以了。
算导以双向链表为例讲解增删查,虽然还是可以通过画图,注意维护涉及节点的prev和next指针指向以及边界条件,能够明白其操作过程,但还是记录下,以备复习之用。
哨兵(sentinel)
哨兵是一个哑对象,其作用是简化边界条件的处理。
类似于以前学习时讲到的头节点。加入哨兵将原来的双向链表转变成一个有哨兵的双向循环两表。L.nil代表哨兵。一图胜千言,如下:
如果有很多个很短的链表,慎用哨兵,因为哨兵所占用的额外存储空间会造成严重的存储浪费。哨兵并没有优化太多的渐进时间界,只是可以使代码更紧凑简洁。
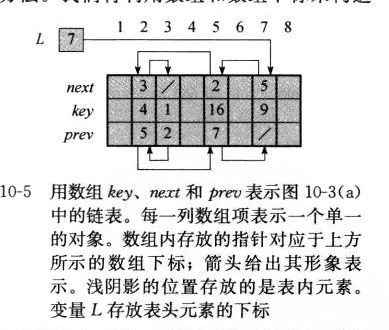
指针和对象的实现
对象的多数组表示:
next和prev中的数字指的是对应数字的下标,有趣!
单数组表示:
对象的分配和释放
略
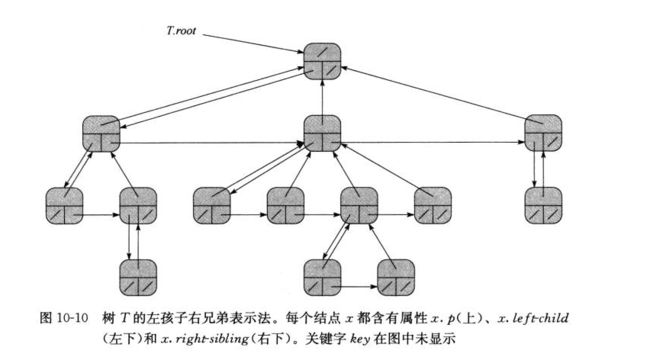
有根树的表示
分支无限制的有根树可以用左孩子右兄弟表示法。
散列表(hash table)
散列表是普通数组概念的推广。
直接寻址表
散列表
直接寻址缺点:如果U全域很大,存储大小为U.size()的一张表T不太实际,而且对于T来讲如果存储的关键字集合K相对于U来说很凶,则T的大部分空间将会浪费掉。
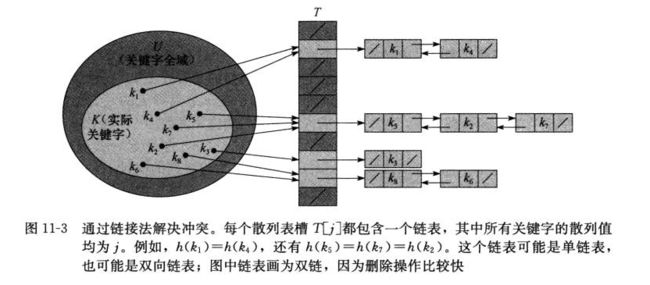
在散列方式(hash)下,关键字k被放到槽(slot)h(k)中,及利用散列函数(hash function)h,根据k计算出槽的位置。这里,函数h将关键字的全域U映射到散列表T[0...m-1]的槽位上(|U|>m,正因如此,完全避免冲突是不可能的)
如果h(k1) = h(k2),则称冲突(collision)
解决冲突的方法
- 链接法(chaining)
关于链接法采用双链的一些解释:来自知乎
简单讲,删除就是从x对应的链表里删除x,双链表的删除加入哨兵只需两行,但是单链表的话只能指定x.next=null,但是在这之前需要先将x.prev.next指向x.next,由于是单链,所以没有prev,只能一直next找下去,相比双链多了查找的时间耗费。
给定一个能存放n个元素的、具有m个槽位的散列表T,定义T的装载因子(load factor)α为n/m,即一个链的平均存储元素数。
散列函数
启发式方法:乘法散列和除法散列
随机技术:全域散列
多数散列函数都假定关键字的全域为自然数集,因此,如果所给的关键字不是自然数,就需要找到一种方法将他们转为自然数。
- 除法散列法
通过取k mod m得余数,将关键字k映射到m个slot上的某一个,h(k) = k mod m
一个不太接近2的整数幂的素数,常常是m的一个较好的选择。
解决冲突方法:开放寻址法(open addressing)
为了使用开放寻址法插入一个元素,需要连续的检查散列表,或称为探查(probe),直到找到一个空槽来放置待插入的关键字为止。
三种技术计算开放寻址法中的探查序列:线性探查、二次探查和双重探查。
这个hash函数应该就是hash(k)= k mod m(m代表散列表的长度)
线性探查,通俗的讲,过程是这样的:利用一个hash函数,计算关键字key位于的槽位下标hash(key),如果T[hash(key)]已经有值,则探查T[hash(key)+1],T[hash(key) +2]直到最后。类似一人找厕所的过程,到一个厕所(hash(key)位置)跟前,看能不能打开门,打不开就挨着找下一个,直到找到对应的位置。(由于就只有m个元素需要hash,则每个都是能找到对应位置的。)
但是,线性探查存在一个问题,称为一次群集(primary clustering)。例如100个槽位,假设后面95位已经被连续占用,下一次hash出来,如果不幸刚好计算出位置在第6位,则需要连续95次才能找到对应的存储槽位,剩下的4次同样也很耗费时间。
二次探查(quadratic probing)
相比于线性探查,在于偏移量采用的是ax^2+bx这种形式
双重散列(double hashing)
是用于开放寻址法的最好方法之一,因为它所产生的排列具有随机选择排列的许多特性。
完全散列
采用两级散列。当关键字集合是静态(即关键字存到表中关键字集合就不再变化了)的,采用完全散列,一级散列于带链接的散列表基本一致,二级散列的长度是存储的关键字个数的平方(主要是为了确保第二级上不出现冲突)。
二叉搜索树
关于树:
- 节点是其本身的祖先和孩子
- 从根节点r到节点x的简单路径上的所有节点y都是x的祖先,如果y≠x,则称y是x的真祖先。(这点同数学上的真子集类似),真后代类似。
- 节点x的孩子数目等于节点x的度
- 根节点r到节点x的条简单路径的长度即为x在有根树T中的深度。
- 节点在树中的高度是指从该节点到叶节点的一条简单路径上边的数目。树的高度也等于树中点的最大深度。
- 如果从根r到节点x的简单路径上最后一条边是(y,x)则称y是x的双亲,x是y的孩子。
- 如果两个节点有相同的双亲,则他们是兄弟。
- 没有孩子的节点称为叶节点(或外部节点),一个非叶节点是内部节点。
- 有序树:是一颗有根树(是一个自由树,其顶点中存在一个与其他顶点不同的顶点),每个节点的孩子是有序的,给孩子标号,这是第一个孩子,那是第二个孩子...
- 自由树:是一个连通的、无环的无向图。称一个可能不连通的无向无环图为森林。
- 满二叉树:每个节点是叶节点或者度为2
- 一个高度为h的完全k叉树的内部节点个数为:k^h-1/(k-1) 完全二叉树有2^h-1个内部节点。
- 完全k叉树:所有叶节点深度相同,且所有内部节点度为k的k叉树(所有节点有k个叉)
注意:《算导》的完全二叉树和满二叉树跟《大话数据结构》里的二者定义完全不同,具体以哪个为准,暂不纠结,哪位朋友知道的,可以告知一下
简介
二叉搜索树的性质:x是一个节点,则其左(右)子树任意节点.key 分别≤(≥)x.key
遍历:
中序遍历(inorder tree walk)子树根的关键字位于左右子树的关键字之间。
前序遍历(preorder tree walk)子树根的关键字位于左右子树的关键字之前。
后序遍历(postorder tree walk)子树根的关键字位于左右子树的关键字之后。
这里区分一下二叉搜索树和最大堆,相同点:比较都是针对所有节点而言,不同点:二叉搜索树,节点左子树值均小于该节点的值,右子树值均小于该节点的值;最大堆:节点值大于所有孩子的值。
查找
O(h),h是这棵树的高度,下面五种操作都是这个复杂度
两种写法:递归和while
最大值和最小值:分别一直查左子树(右子树)即可
后继(successor)和前驱(predecessor):
后继:两种情况,如果x的右子树不为空,则右子树中的最小值就是x的后继; 反之,一直找x的双亲节点,直到x是y的左子树为止。
插入和删除
插入和删除会引起由二叉搜索树表示的动态集合的变化,一定要修改数据结构来反映这个变化,但修改要保持二叉搜索树性质的成立。
插入:
边界条件,二叉搜索树没有元素;否则找到新插入节点z插入的位置的双亲节点。
删除:
三种基本策略:
- z没有孩子节点,就只是简单的将它删除,并修改它的父节点,用NIL作为孩子来替换z。
- 如果z只有一个孩子,那么将这个孩子提升到树中z的位置上,并修改z的父节点,用z的孩子来替换z。
-
如果z有两个孩子,那么找z的后继y(一定在z的右子树中),并让y占据树中z的位置。z的原来右子树部分成为y的新的右子树,并且z的左子树成为y的新的左子树,这种情况稍显麻烦,因为还与y是否为z的右孩子相关。
随机构建二叉搜索树
略
BST(binary search tree)的基本操作大都能在O(h)时间内完成。
红黑树(red-black tree)
红黑树是许多平衡搜索树中的一点,可以保证最坏情况下基本动态集合操作的时间复杂度为O(nlgn)。
红黑树是一颗二叉搜索树,增加了颜色,RED or BLACK,确保了没有一条路径会比其他路径长出2倍,因而是近似于平衡的。
相比BST的属性p,left,right,key多了一个属性color。
红黑树的一些特性:
- 每个节点是红色或是黑色
- 根节点是黑色的
- 每个叶节点(NIL)是黑色的
- 如果一个节点是红色的,则它的两个子节点都是黑色的
- 对每个节点,从该节点到其所有后代叶节点的简单路径上,均包含相同数目的黑色节点。
使用一个哨兵(sentinel)T.NIL代表所有的NIL
从某个节点x出发(不含该节点)到达一个叶节点的任意一条简单路径上的黑色节点个数称为该节点的黑高(black-height),记作bh(x)
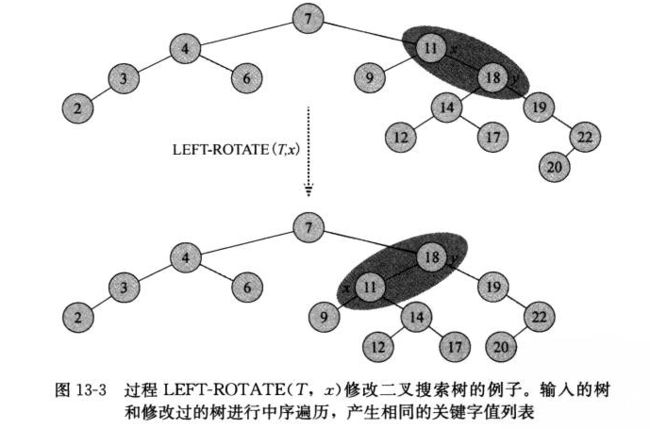
旋转
进行增删的时候可能会破坏上面提到的5条性质,因此为了维护这些性质,必须改变某些节点的颜色及指针结构。
指针结构的修改是通过旋转(rotation)来完成的。
这里的左旋和右旋似乎跟《大话数据结构》里AVL树的左旋右旋有相似之处。
一图胜千言:
要理解各个指针的改变,下面这个图好好看下:
插入
插入耗费时间O(lgN),且该程序选择不超过两次
插入一个节点z,并将其着色为红色。
插入后的修补工作:
while的结束条件是当z的双亲节点颜色是黑色时
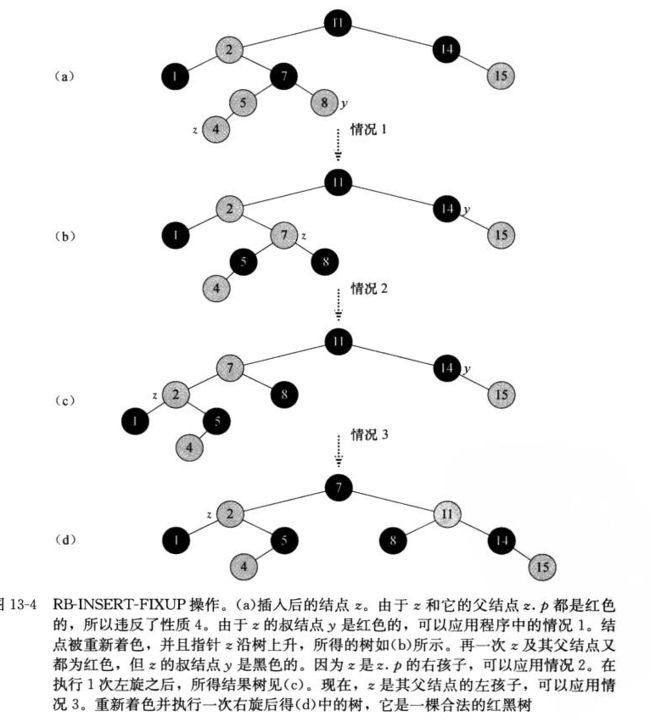
fixup例子:(阴影部分为黑色)
插入操作只可能破坏红黑树性质2和性质4,并且只能破坏其中一条。
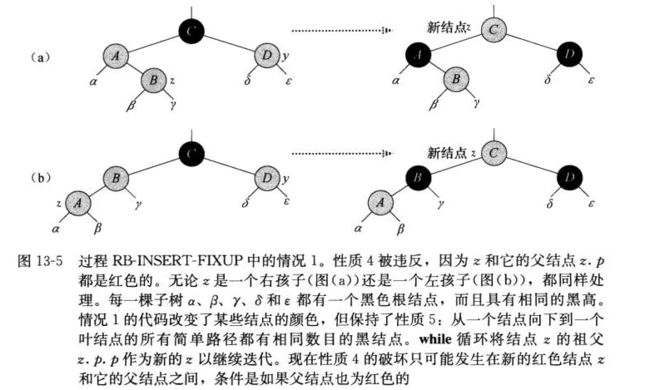
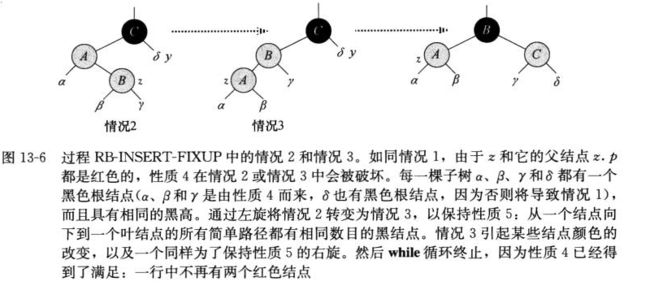
修补的三种情况分析:
case 1:z的叔节点y是红色的
此时,不需要旋转,只需要改变颜色,z指向z.p.p即可
z.p.color = y.color = black;
z.p.p.color = red;
case2:z的叔节点y是黑色的且z是一个右孩子
case3:z的叔节点y是黑色的且z是一个左孩子
情况2通过一次左旋转成case3。
z.p.color = black;
z.p.p.color=red;
再一次右旋
删除
删除节点耗费O(lgN)时间。
需要提供一个让某节点孩子来接替老子位置的一个方法transplant
删除方法:
1-8行是子承父位,9行是找出z的后继,10-20行维护了相关的一些指针指向(将y的右孩子移到y的位置,y移到z的位置),21-22行如果z孩子小于2个,z的颜色是黑色(这种情况很简单,结合红黑树性质5分析)或者z孩子有两个,z的后继是黑色,则进行修正(画图理解最清楚了,比较简单就不画了)。为什么修正呢,因为当是黑色的时候,会破坏红黑树性质5,影响黑高。
来看下删除修复过程:
删除修复例子:
删除的四种case:
case1:x的兄弟节点w是红色的
过程:w描黑,x.p描红,x.p左旋,维持w兄弟指针指向
case2:x的兄弟节点w是黑色的,w的两个子节点都是黑色的
w描红,x指向x.p
case3:x的兄弟节点w是黑色的,w的孩子左红右黑
w左孩子描黑,w描红,w右旋,w指向x.p.right,仍旧是维持兄弟指针指向
case4:x的兄弟节点w是黑色的,w的右孩子是红色的
修改w颜色同x.p颜色一致,x.p描黑,w右孩子描黑,结束循环。
关于删除的一些深入理解,参考 图解红黑树(别看评论,笑点低的会觉得搞笑的 _)
了解了散列(hash)和红黑树,就可以去愉快的看下Java里面HashMap的源码啦。
AVL(树)
节点左右子树高度相差至多为1.
未深入讲解。
B树
为磁盘存储而专门设计的一类平衡搜索树。B树类似于红黑树,但它们在降低磁盘I/O操作数方面要更好一些,许多数据库系统使用B树或者B树变种来存储信息。比如MySQL数据库使用了B+树的数据结构。
B+相比B树来说,主要有几个区别,B+树叶子节点存储了所有数据,可以只经过一次遍历;叶子节点构成了一个单向链表。至于B树的插入删除等,参考2-3树更容易理解一些。
关于B树和B+树的区别等可以参加B树和B+树的区别
B-tree,B+tree,想起以前还以为是一个B+,一个B-呢,哈哈
辅存上的数据结构
计算机的主存(primary memory或main memory)通常由硅存储芯片组成。相比辅存比如磁盘磁带价格高,容量小,而辅存容量大价格低然而速度也要慢一些。(这方面的知识哪天还得看下计算机组成原理,虽然《计算机科学导论》也讲过一些,但总觉得还差点东西)
磁盘慢,主要是因为有机械运动的部分:盘片旋转和磁臂移动。
本书第三版,2009年出版,这时磁盘旋转速度是5400~15000转/分钟(RPM),通常15000RPM的速度是用于服务器级的驱动器上,7200RPM的速度用于台式机的驱动器上,5400RPM的速度用于笔记本的驱动器上。随便在jd上看了机械硬盘和固态硬盘,机械硬盘缓存64MB左右,一款三星SSD缓存在512MB,读写在百兆/s。
7200RPM旋转一圈需要8.33ms,比硅存储的常见存取时间50ns要高出5个数量级(10的5次方)。也就是说,这个时间内,可能存取主存超过100000次。
为了瘫痪机械移动所花费的等待时间,磁盘会一次存取多个数据项而不是一个。信息被分为一系列相等大小的在柱面内连续出现的位页面(page),并且每个磁盘读或写一个或多个完整的页面。对于一个典型的磁盘来说,一夜的长度可能为2 11~214字节。
这里,对运行时间的两个主要组成成分分别加以考虑:磁盘存取次数和CPU(计算)时间。
定义
所有叶节点深度相同,即树高h;每个节点所包含的关键字个数有上界和下界,用一个被称为B树的最小度数的固定证书t≥2来表示这些界:每个节点除根节点外必须至少有t-1个关键字,至多可以包含2t-1个关键字。
B+tree将卫星数据存储到叶节点上,内部结点只存放关键字和孩子指针。对存储在磁盘上的一颗大的B树,通常看到分支因子在50~2000之间。
基本操作
约定:1. B树的根节点始终在主存中,这样无需对根做DISK-READ操作;然而,当根节点被改变后,需要对根节点做一次DISK-WRITE操作。2. 任何被当做参数的节点在被传递之前,都要对他们先做一次DISK-READ操作。
-
搜索B树
先从x节点内部关键字查找,找不到,并且x有孩子的话或不是叶节点,再从x.ci孩子节点查找。
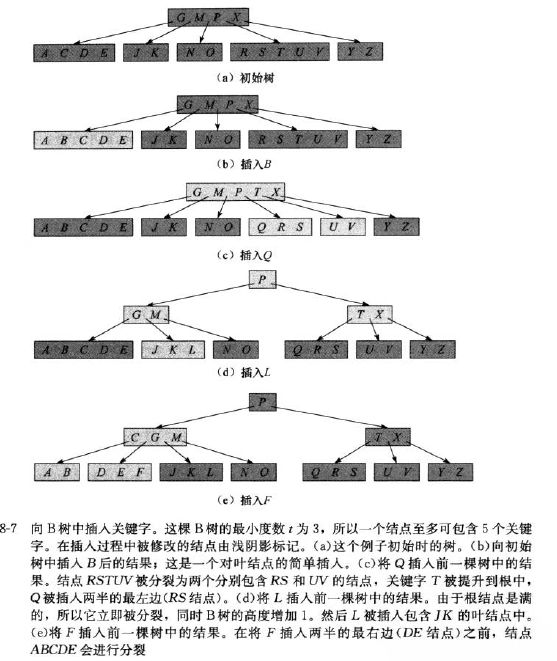
向B树中插入一个关键字
由于不能向满的叶节点插入节点,故引用分裂操作,将满的叶节点(2t-1)分割为两个(t-1)关键字的节点,中间关键字被提升到y的父节点。从树根往下查找关键字所属位置时,就分裂沿途遇到的每一个满节点。-
分裂B树中的节点
分裂是树长高的唯一途径。
以沿树单程下行方式向B树插入关键字
2-8行处理x是叶节点的情况,9-12行找到合适的位置,如果ci子节点已满,则进行split操作,15-16行确定应该具体插入那个ci节点,17行递归插入。
这里提到一点,insert-nonfull是尾递归的,所以它可以用一个while循环来实现(这里也是一个重要的知识点,改天再找资料尝试一下)
图解插入:
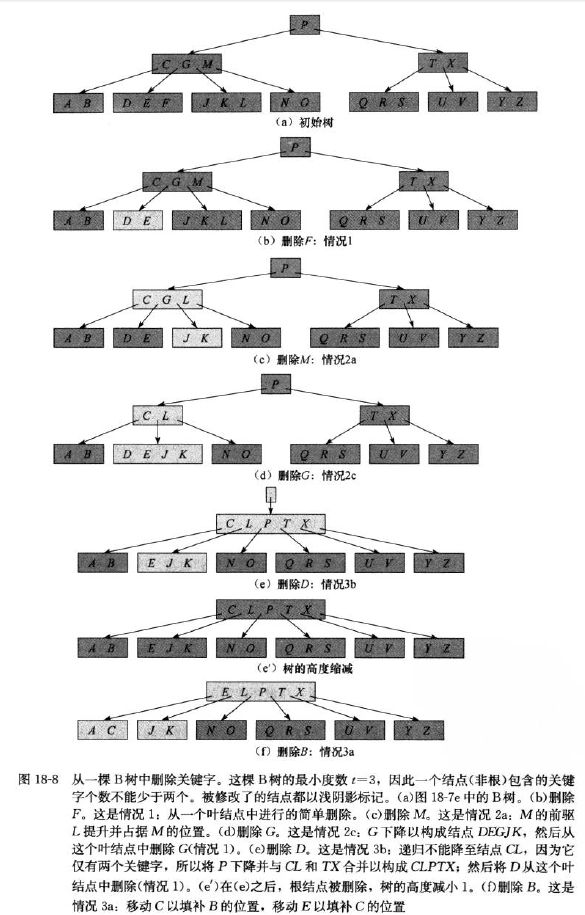
从B树中删除关键字
根节点允许有比最少关键字数t-1还少的关键字个数。
当要删除关键字的路径上节点(非根)有最少的关键字个数时,也可能需要向上回溯。
删除实例:
删除比较复杂一点,case1,case2a,2b,2c,case3a,3b.
递归调用自身时,必须保证该节点至少有t个关键字
高级设计和分析技术
动态规划(dynamic programming)
这里,programming指的是一种表格法,并非编写计算机程序
动态规划方法通常用来求解最优化问题(optimization problem)
似乎跟高中学习的求最优解的问题有相似之处。
按如下4个步骤来设计动态规划算法:
- 刻画出一个最优解的结构特征
- 递归的定义最优解的值
- 计算最优解的值,通常采用自底向上的方法
- 利用计算出的信息构造一个最优解
最优子结构(optimal substructure)性质:问题的最优解由相关子问题的最优解组合而成,而这些子问题可以独立求解,主要原因是:反复求解相同的子问题,同斐波那契数列基本递归一样。
动态规划方法仔细安排求解顺序,对每个子问题只求解一次,并将结果保存下来。此乃时空权衡(time-memory-trade-off)。
自顶向下递归实现:时间复杂度(2^n)
动态规划有两种等价的实现方法:
-
带备忘的自顶向下法(top-down with memoization)
仍按自然递归形式编写过程,但过程会保存每个子问题的解(通常保存在一个数组或散列表中)
MEMOIZED-CUT-ROD(p,n)仅仅用来初始化一个存储计算值的数组,主要实现在AUX那个方法里。
借鉴了下别人的思想,尾递归写法如下:
public int getFibonacciWithTailRecursive(int num, int pp, int prev) {
if (num == 0) {
return pp;
}
return getFibonacciWithTailRecursive(num - 1, prev, pp + prev);
}
-
自底向上法(bottom-up method)
在求解某个子问题时,它所依赖的那些更小的子问题都已求解完毕,结果已经保存。
按照这种思想写了一下斐波那契数列的自底向上实现:
public int getFibonacciNum(int num) {
int[] tmp = new int[num + 1];
for (int i = 0; i <= num; i++) {
switch (i) {
case 0:
tmp[i] = 0;
break;
case 1:
tmp[i] = 1;
break;
default:
tmp[i] = tmp[i - 1] + tmp[i - 2];
}
}
return tmp[num];
}
此种写法有改进空间,由于计算第n个数只需要前面n-1和n-2的值即可,所以可以改进为只用两个变量存储,类似于这位朋友所写点击查看
试了下a,b这种形式,发现速度更慢了,还不如原始上面这种版本。
关于斐波那契数列的这些写法,用额外的数组存储已经计算过的斐波那契数,利用额外的存储空间换来的是时间上的飞跃,所谓空间换时间。
public int getFibonacciNum2(int num) {
int pp = 0, prev= 1;
int tm = 0;
for (int i = 2; i < num; i++) {
tm = prev + pp;
pp = prev;
prev = tm;
}
return pp + prev;
}
另外写了个测试类,比较了一下尾递归、自底向上和普通递归
@Test
public void test() {
int num = 300;
long start2 = System.nanoTime();
int fibonacciNum2 = getFibonacciNum2(num);
System.err.println(fibonacciNum2);
System.err.println("自底向上花费:" + (System.nanoTime() - start2));
System.err.println("-----------------");
long start3 = System.nanoTime();
int fibonacciNum3 = getFibonacciWithTailRecursive(num, 0, 1);
System.err.println(fibonacciNum3);
System.err.println("尾递归花费:" + (System.nanoTime() - start3));
System.err.println("-----------------");
long start = System.nanoTime();
int fibonacciNum = getFibonacciNum(num);
System.err.println(fibonacciNum);
System.err.println("普通递归:" + (System.nanoTime() - start));
System.err.println("-----------------");
}
/**
* 自底向上
* @param num
* @return
*/
public int getFibonacciNum2(int num) {
int[] tmp = new int[num + 1];
for (int i = 0; i <= num; i++) {
switch (i) {
case 0:
tmp[i] = 0;
break;
case 1:
tmp[i] = 1;
break;
default:
tmp[i] = tmp[i - 1] + tmp[i - 2];
}
}
return tmp[num];
}
/**
* 普通递归
* @param num
* @return
*/
public int getFibonacciNum(int num) {
if (num == 0) return 0;
if (num == 1) return 1;
return getFibonacciNum(num - 1) + getFibonacciNum(num - 2);
}
public int getFibonacciWithTailRecursive(int num, int pp, int prev) {
if (num == 0) {
return pp;
}
return getFibonacciWithTailRecursive(num - 1, prev, pp + prev);
}
最后发现,尾递归在num=100时,是用a,b存储的自底向上的时间的1/3,略微优于最初的自底向上版本,这三种方式都完全优于一般递归。
言归正传,继续学习。
矩阵链乘法(跳过)
动态规划原理(跳过)
最长公共子序列(LCS)
简单讲,Z={B,C,D,B}是X={A,B,C,B,D,A,B}的子序列,对应的下标序列是{2,3,5,7}
最长公共子序列问题(longest-common-subsequence problem)
求解过程:
首先,解释一下“前缀”,给定一个序列X=(x1,x2,...,xm)对i=0,1,...m,定义X的第i前缀为Xi= (x1,x2,...,xi)X0为空串。
-
刻画LCS的特征
- 一个递归解
给出了一个求LCS长度的函数 -
计算LCS的长度
总体来说,构成一条路径
最优二叉搜索树(跳过,不过这里可能如果后面有需要还是可以学习一下)
贪心算法
假定每一步都选取最优解,达到最终最优解。
活动选择问题
摊还分析(跳过)
《算法导论》阅读学习,至此完结。还剩下几个计数排序,再找时间学习了。