深度学习手记（五）之优化方法

梯度下降和反向传播算法是神经网络模型的主要优化算法。梯度下降算法主要用于优化单个参数的取值而反向传播算法给出了一个高效的方式在所有参数上使用梯度下降算法，从而使神经网络的损失函数尽可能的小。在这里就不具体对梯度下降算法仔细讲解了（网上资源很多），主要对深度学习神经网络优化过程做一个介绍。
对于梯度下降算法，我们不得不说到梯度和学习率的设置，参数的梯度可以通过求偏导的方式计算得到，有了梯度还需要定义一个学习率。可以简单的理解为学习率就是梯度下降的步长，这个步长太大太小都不好。如果太大了，就会导致参数在极优值的两侧来回移动，得不到最佳参数；如果太小了，就会导致模型训练变慢，很长时间都不能达到最优参数。
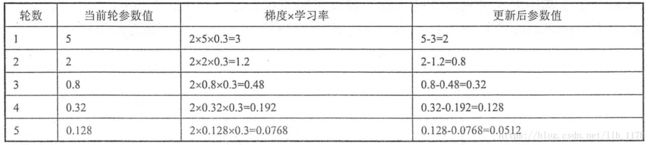
下面通过一个例子说明梯度下降是怎么工作的。假如损失函数为f(x)=x^2，要对参数x进行优化。那么第一步随机生成一个x的初始值和给定一个学习率并且计算学习梯度(对损失函数求偏导得梯度为2)，第二步通过梯度和学习率（计算公式：）来更新参数x。假设参数的初始值为5，学习率为0.3，那么可以得到：

但是，如果我们将学习率的初始值设的太大呢？就会出现下面的局面：

在最优解参数前后来回移动。

---

所以，也要对学习率进行优化，常用的方法是指数衰减法，通过这个方法可以使较大的学习率快速得到一个比较优的解，然后随着迭代的继续逐步减小学习率，使得模型在训练后期更加稳定。
同时呢，在考虑优化损失函数时，也应该考虑另外一个问题过拟合的问题。我们不是以训练模型为目的而是用模型预测未知数据，也就是说模型的泛化能力才是关键，所以，过拟合是必须要考虑的事情。为了避免过拟合问题，一个非常常用的方法是正则化。正则化的思想就是控制权重参数，使得模型不能任意拟合训练数据中的随机噪声。常见的正则有L1和L2，L1使参数变得更稀疏，而L2不会。
说了这么说，接下来我们就来实战一个数据集fashion-mnist，通过添加梯度下降、指数衰减学习率、正则化、dropout、batch方法优化数据集。
首先，简单介绍一下此数据集，它分为train和test集，包含了一共10个类别的服饰的几万张28x28的灰色图像，类似于mnist数据集。

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.cm as cm
%matplotlib inline

train_data = pd.read_csv("fashion-mnist_train.csv")
train_data.shape

(60000, 785)

train_data.head()

labels = np.unique(train_data["label"])
labels

array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9], dtype=int64)

images = train_data.iloc[:,1:].values
images = images.astype(np.float)
# convert from [0:255] => [0.0:1.0]
images = np.multiply(images, 1.0 / 255.0)
images_size = images.shape[1]
images_width = images_height = np.ceil(np.sqrt(images_size)).astype(np.uint8)
# 可视化
def display(img):
    one_image = img.reshape(images_width, images_height)
    plt.axis("off")
    plt.imshow(one_image, cmap=cm.binary)
# 随便取一张图像
display(images[10])
plt.show()

通过上面操作，可视化第10张图像。
接下来进行神经网络模型训练：

train_data = pd.read_csv("fashion-mnist_train.csv")
test_data = pd.read_csv("fashion-mnist_test.csv")
# print(train_data.shape)
# print(test_data.shape)
## 参数设置
# 输入层的节点数
INPUT_NODE = 784
OUTPUT_NODE = 10
# 隐藏层的节点数，这里使用只有一个隐藏层的网络结构作为样例，这个隐藏层有500个节点。
LAYER1_NODE = 500
# 一个训练batch中的训练数据的个数。数字越大，训练越接近梯度下降，数字越小，训练程度接近随机梯度下降。
BATCH_SIZE = 80
# 基础的学习率
LEARNING_RATE_BASE = 0.4
# 学习率的衰减率，越大模型越趋于稳定
LEARNING_RATE_DECAY = 0.99
# 描述模型复杂度的正则化项在损失函数中的系数
REGULARIZATION_RATE = 0.0001
# 训练的循环数
TRAINING_STEPS = 30000
# 标准化训练集
train_images = train_data.iloc[:, 1:].values
train_images = train_images.astype(np.float)
train_images = np.multiply(train_images, 1.0 / 255.0)
# 标准化测试集
test_images = test_data.iloc[:, 1:].values
test_images = test_images.astype(np.float)
test_images = np.multiply(test_images, 1.0 / 255.0)
#输出
print('train images({0[0]},{0[1]})'.format(train_images.shape))
print('test images({0[0]},{0[1]})'.format(test_images.shape))

train images(60000,784)
test images(10000,784)

#定义一个one-hot编码函数
def dense_to_one_hot(labels_dense, num_classes):
    num_labels = labels_dense.shape[0]
    index_offset = np.arange(num_labels) * num_classes
    labels_one_hot = np.zeros((num_labels, num_classes))
    labels_one_hot.flat[index_offset + labels_dense.ravel()] = 1
    return labels_one_hot

#对train和test的labels进行one hot编码
train_labels_flat = train_data[["label"]].values.ravel()
train_labels_count = np.unique(train_labels_flat).shape[0]

test_labels_flat = test_data[["label"]].values.ravel()
test_labels_count = np.unique(test_labels_flat).shape[0]

train_labels = dense_to_one_hot(train_labels_flat, train_labels_count)
train_labels = train_labels.astype(np.uint8)

test_labels = dense_to_one_hot(test_labels_flat, test_labels_count)
test_labels = test_labels.astype(np.uint8)

print(train_labels.shape)
print(train_labels[0])

print(test_labels.shape)
print(test_labels[0])

(60000, 10)
[0 0 1 0 0 0 0 0 0 0]
(10000, 10)
[1 0 0 0 0 0 0 0 0 0]

# 设置一部分验证集
VALIDATION_SIZE = 10000
validation_images = train_images[:VALIDATION_SIZE]
validation_labels = train_labels[:VALIDATION_SIZE]

train_images = train_images[VALIDATION_SIZE:]
train_labels = train_labels[VALIDATION_SIZE:]

#train_images = train_images.reshape(train_images.shape[0], img_rows, img_cols, 1)
#validation_images = validation_images.reshape(validation_images.shape[0], img_rows, img_cols, 1)


print('train_images({0[0]},{0[1]})'.format(train_images.shape))
print('train_labels({0[0]},{0[1]})'.format(train_labels.shape))
print('validation_images({0[0]},{0[1]})'.format(validation_images.shape))
print('validation_labels({0[0]},{0[1]})'.format(validation_labels.shape))

train_images(50000,784)
train_labels(50000,10)
validation_images(10000,784)
validation_labels(10000,10)

# 设置神经网络，这里只用一层隐藏层。
weight1 = tf.Variable(tf.truncated_normal([INPUT_NODE, LAYER1_NODE], stddev=0.1))
weight2 = tf.Variable(tf.truncated_normal([LAYER1_NODE, OUTPUT_NODE], stddev=0.1))
biase1 = tf.Variable(tf.constant(0.1, shape=[LAYER1_NODE]))
biase2 = tf.Variable(tf.constant(0.1, shape=[OUTPUT_NODE]))
# 设置输入和输出变量
x = tf.placeholder("float32", shape=(None, INPUT_NODE))
y_ = tf.placeholder("float32", shape=(None, OUTPUT_NODE))
keep_prob = tf.placeholder('float32')
global_step = tf.Variable(0, trainable=False)
# 神经网络层与层之间的运算
a = tf.nn.relu(tf.matmul(x, weight1) + biase1)
y = tf.matmul(a, weight2) + biase2 
# 设置损失函数，bp算法对全局参数进行更新优化
loss = tf.nn.sparse_softmax_cross_entropy_with_logits(labels=tf.argmax(y_,1), logits=y)
# 设置L2正则优化
regularizer = tf.contrib.layers.l2_regularizer(REGULARIZATION_RATE)
regularization = regularizer(weight1) + regularizer(weight2)
loss = tf.reduce_mean(loss) + regularization
# 设置指数衰减学习率函数
learning_rate = tf.train.exponential_decay(LEARNING_RATE_BASE, global_step, train_images.shape[0] / BATCH_SIZE, LEARNING_RATE_DECAY)
# 设置梯度下降算法进行优化
train_step = tf.train.GradientDescentOptimizer(learning_rate).minimize(loss, global_step=global_step)
# 计算正确率
correct_prediction = tf.equal(tf.argmax(y,1), tf.argmax(y_,1))
accuracy = tf.reduce_mean(tf.cast(correct_prediction, 'float32'))

# 定义batch，一个批次一个批次的进行训练
epochs_completed = 0
index_in_epoch = 0
num_examples = train_images.shape[0]

# serve data by batches
def next_batch(batch_size):

    global train_images
    global train_labels
    global index_in_epoch
    global epochs_completed

    start = index_in_epoch
    index_in_epoch += batch_size

    # when all trainig data have been already used, it is reorder randomly    
    if index_in_epoch > num_examples:
        # finished epoch
        epochs_completed += 1
        # shuffle the data
        perm = np.arange(num_examples)
        np.random.shuffle(perm)
        train_images = train_images[perm]
        train_labels = train_labels[perm]
        # start next epoch
        start = 0
        index_in_epoch = batch_size
        assert batch_size <= num_examples
    end = index_in_epoch
    return train_images[start:end], train_labels[start:end]

最后，开始运行神经网络：

# 创建会话，开始执行。
init = tf.initialize_all_variables()
sess = tf.Session()
sess.run(init)
# print(sess.run(weight1))

for i in range(TRAINING_STEPS):
    batch_xs, batch_ys = next_batch(BATCH_SIZE)    
    sess.run(train_step, feed_dict={x: batch_xs, y_: batch_ys})
    if i % 1000 == 0:
        validata_acc = sess.run(accuracy, feed_dict={x: validation_images, y_: validation_labels})
        print("After %d training step(s), validation accuracy using average model on validation data is %g" % (i, validata_acc)) 

test_acc = sess.run(accuracy, feed_dict={x:test_images, y_:test_labels})
print("After %d training step(s), test accuracy using average model is %g" % (TRAINING_STEPS, test_acc))

到此，将所有代码写完包括，添加正则和指数衰减学习率方法的实现。下面再将自己跑的结果附在下面。效果不好，可能原因是参数还不够优化，此外这个数据集可能用CNN要好一点。但是，由于初步学习深度学习，没有直接使用CNN等高级的深度学习模型，只是想巩固一下对一般神经网络的学习和理解。希望大家给我意见和指导！
正则和指数衰减学习率什么都不加：

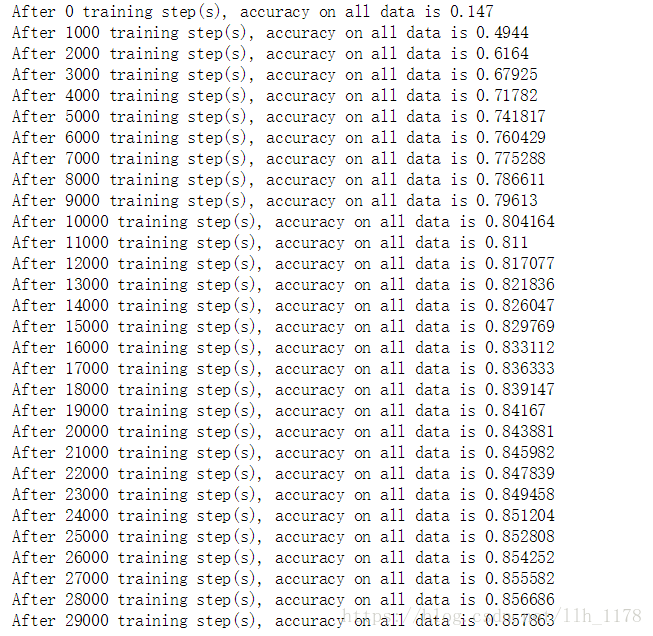
加入biase后：

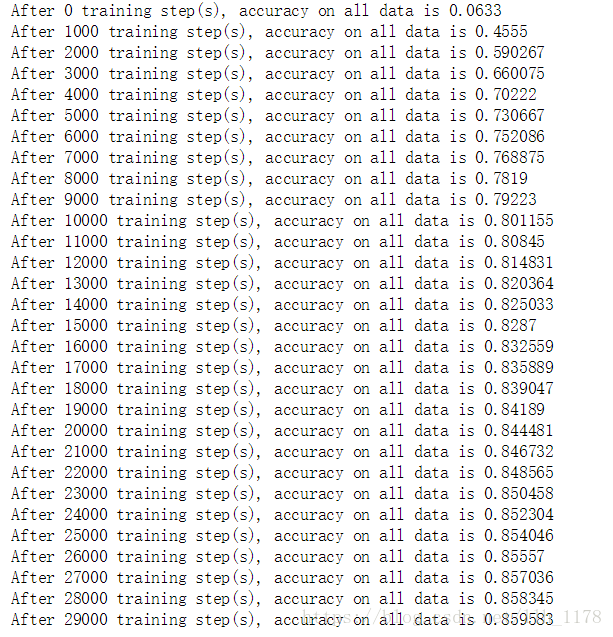
去掉dropout之后（我之前是加上的是为了防止过拟合，但是，我发现如果对这样简单的神经网络用dropout反而不好，会欠拟合）：

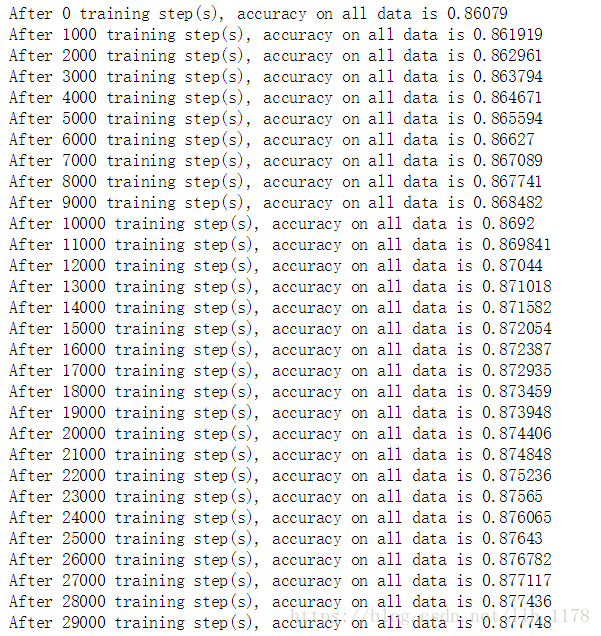
使用正则和指数衰减学习率：

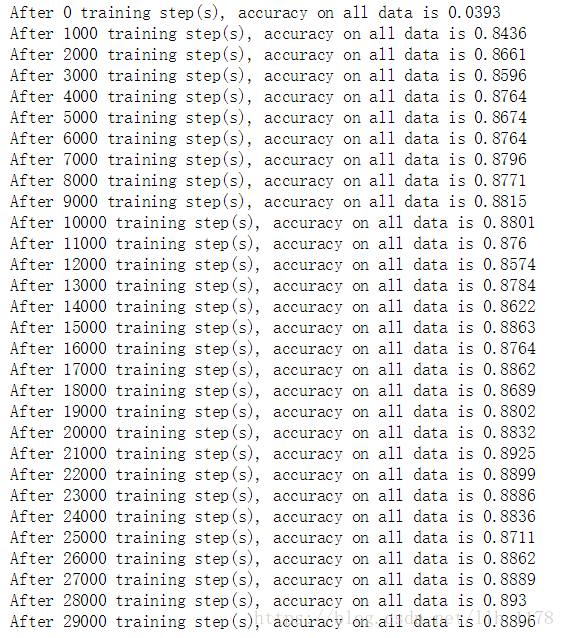
用测试集进行验证：

可以，看出在训练集和测试集上的结果还是有差异的，但是，我们是希望这种差异越小越好，因为这样泛化能力越强。
然后，我将初始学习率降低到0.5:

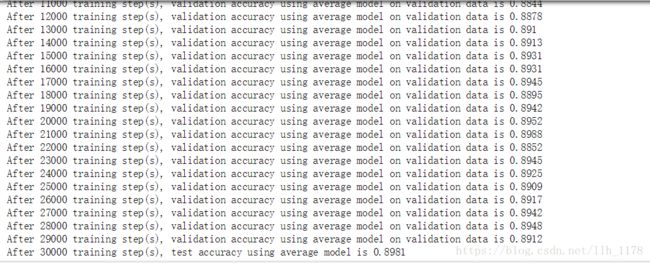
最后，我又将batch_size从100降低到80：

跟前一个比，感觉测试集和训练集上的结果都降低了一点点，但是，他们的差异也变小了，所以，我觉得总体上比上一个模型好一点点。但是，这所有的测试呢，都不怎么高，还有有待进步！