mrcrack
mrcrack

BZOJ刷题记录---普及组难度 AC

BZOJ刷题记录---普及组难度

总目录详见https://blog.csdn.net/mrcrack/article/details/90228694

序号 题号 算法 思想难度 实现难度 总难度 推荐指数
1 2659 数学 20 7 27 2
2 1968 枚举 15 13 28 2
3 2761 去重 12 18 30 6
4 3767 高精度A+B 10 20 30 2
5 1432 找规律 27 5 32 3
6 3098 随机卡HASH 23 10 33 2
7 1800 统计 20 16 36 3
8 1218 枚举 20 17 37 2
9 4001 找规律 28 9 37 3
10 2760 字符串处理 12 26 38 1
11 1088 DP/判断 22 17 39 6
12 1034 贪心 24 16 40 6
13 1207 DP 23 17 40 2
14 2748 DP 21 19 40 4
15 4302 分类讨论 29 11 40 　
16 1083 最小生成树 17 25 42 9
17 2563 转换后排序 27 15 42 7
18 3097 构造卡HASH 27 15 42 2
19 1022 简单博弈 30 13 43 3
20 2465 贪心 25 20 45 4
21 2122 暴力 28 18 46 2
22 1197 DP 31 19 50 2
23 1295 搜索 20 30 50 5
24 1821 最小生成树 25 25 50 4
25 2134 期望DP 30 20 50 4

测评地址：

1.bzoj 2659  //2659: [Beijing wc2012]算不出的算式   //在线测评地址https://www.lydsy.com/JudgeOnline/problem.php?id=2659

2.bzoj 1968   //1968: [Ahoi2005]COMMON 约数研究   //在线测评地址https://www.lydsy.com/JudgeOnline/problem.php?id=1968

3.bzoj 2761   //2761: [JLOI2011]不重复数字   //在线测评地址https://www.lydsy.com/JudgeOnline/problem.php?id=2761

4.bzoj 3767   此题存在版权，故不再支持提交，保留在此只供大家参考题面！ 望见谅！

5.bzoj 1432   //1432: [ZJOI2009]Function   //在线测评地址https://www.lydsy.com/JudgeOnline/problem.php?id=1432

6.bzoj 3098   //3098: Hash Killer II   //在线测评地址https://www.lydsy.com/JudgeOnline/problem.php?id=3098

7.bzoj 1800   //1800: [Ahoi2009]fly 飞行棋   //在线测评地址https://www.lydsy.com/JudgeOnline/problem.php?id=1800

8.bzoj 1218   //1218: [HNOI2003]激光炸弹   //在线测评地址https://www.lydsy.com/JudgeOnline/problem.php?id=1218

9.bzoj 4001   //4001: [TJOI2015]概率论   //在线测评地址https://www.lydsy.com/JudgeOnline/problem.php?id=4001

10.bzoj 2760   //2760: [JLOI2011]小A的烦恼   //在线测评地址https://www.lydsy.com/JudgeOnline/problem.php?id=2760

11.bzoj 1088   //1088: [SCOI2005]扫雷Mine   //在线测评地址https://www.lydsy.com/JudgeOnline/problem.php?id=1088 

12.bzoj 1034   //1034: [ZJOI2008]泡泡堂BNB   //在线测评地址https://www.lydsy.com/JudgeOnline/problem.php?id=1034

13.bzoj 1207   //1207: [HNOI2004]打鼹鼠   //在线测评地址https://www.lydsy.com/JudgeOnline/problem.php?id=1207 

14.bzoj 2748   //2748: [HAOI2012]音量调节   //在线测评地址https://www.lydsy.com/JudgeOnline/problem.php?id=2748

15.bzoj 4302   //4302: Hdu 5301 Buildings   //在线测评地址https://www.lydsy.com/JudgeOnline/problem.php?id=4302

16.bzoj 1083   //1083: [SCOI2005]繁忙的都市   //在线测评地址https://www.lydsy.com/JudgeOnline/problem.php?id=1083

17.bzoj 2563   //2563: 阿狸和桃子的游戏   //在线测评地址https://www.lydsy.com/JudgeOnline/problem.php?id=2563

18.bzoj 3097   //3097: Hash Killer I   //在线测评地址https://www.lydsy.com/JudgeOnline/problem.php?id=3097

19.bzoj 1022 //1022: [SHOI2008]小约翰的游戏John   //在线测评地址https://www.lydsy.com/JudgeOnline/problem.php?id=1022

20.bzoj 2465   //2465: [中山市选2009]小球   //在线测评地址https://www.lydsy.com/JudgeOnline/problem.php?id=2465

21.bzoj 2122   //2122: 工作评估   //在线测评地址https://www.lydsy.com/JudgeOnline/problem.php?id=2122

22.bzoj 1197   //1197: [HNOI2006]花仙子的魔法   //在线测评地址https://www.lydsy.com/JudgeOnline/problem.php?id=1197

23.bzoj 1295   //1295: [SCOI2009]最长距离   //在线测评地址https://www.lydsy.com/JudgeOnline/problem.php?id=1295

24.bzoj 1821   //1821: [JSOI2010]Group 部落划分 Group   //在线测评地址https://www.lydsy.com/JudgeOnline/problem.php?id=1821

25.bzoj 2134   //2134: 单选错位   //在线测评地址https://www.lydsy.com/JudgeOnline/problem.php?id=2134

题解：

1.bzoj 2659  //2659: [Beijing wc2012]算不出的算式   //在线测评地址https://www.lydsy.com/JudgeOnline/problem.php?id=2659

//2659: [Beijing wc2012]算不出的算式
//在线测评地址https://www.lydsy.com/JudgeOnline/problem.php?id=2659 
//可能遇到int溢出，采用unsigned long long 
//样例通过，提交Time_Limit_Exceed，顿时傻眼。 
//看来要用等差数列求和公式，被公式中的字母迷惑了。 
//马上修改,发现，遇到了取整的问题。难办啊2019-5-19 22:21 
//https://www.cnblogs.com/zhber/p/4116413.html此文思路写得不错
//先画出个坐标系，标出坐标为(p,q)的点，然后从(0,0)到(p,q)连一条线，画出以这条线为对角线的长方形。显然直线的斜率是p/q。
//你会发现Σ[kp/q]其实就是直线下方的整点数，而Σ[kq/p]就是直线上方的整点数。
//计算p==q的时候还要考虑直线上有整点的情况
//说实话，打表，探得公式，其实很困难。 
//样例解释如下：

BZOJ刷题记录---普及组难度 AC_第1张图片

//样例通过，提交Wrong_Answer，阅读代码，发现
//else printf("%llu\n",(1+(p-1)/2)/2*(p-1)/2+(1+(q-1)/2)/2*(q-1)/2);//此处写成else printf("%llu\n",(1+(p-1)/2)*(p-1)/2+(1+(q-1)/2)*(q-1)/2);//等差数列，求和 
//提交AC。2019-5-20 22:09
//bzoj是ACM提交模式。 
 
#include
#define ULL unsigned long long
int main(){
    ULL p,q,k,L,sum=0;
    scanf("%llu%llu",&p,&q);
    if(p!=q)printf("%llu\n",(p-1)*(q-1)/4);
    else printf("%llu\n",(1+(p-1)/2)/2*(p-1)/2+(1+(q-1)/2)/2*(q-1)/2);//此处写成else printf("%llu\n",(1+(p-1)/2)*(p-1)/2+(1+(q-1)/2)*(q-1)/2);//等差数列，求和 
    return 0;
}

2.bzoj 1968   //1968: [Ahoi2005]COMMON 约数研究   //在线测评地址https://www.lydsy.com/JudgeOnline/problem.php?id=1968

//1968: [Ahoi2005]COMMON 约数研究
//在线测评地址https://www.lydsy.com/JudgeOnline/problem.php?id=1968
//0 < N < 1000000要么O(logn)，要么O(nlogn)
//想到了 素数筛，想到了 约数成对出现 还想到了质因数分解6=2^1*3^1  约数个数(1+1)*(1+1)=4
//先写个素数筛 还不错，能独立写出。2019-5-21
//质数的约数为2，和数的约数分解质因数来处理
//2^20=1024*1024，故具体到某个数，阶数不超过20，故在筛的过程中，再计算 阶数 ,不超时，极限是20*10^6=2*10^7
//n=1无需特判，可读程序，即明白。
//测试了n=1000000,输出13970034，发现，还是要超时
//将以下两句进行优化
//for(j=1;j<=cnt;j++)
//    if(x%prime[j]==0)break;
//改成 while(x%prime[j])j++;
//测试了，n=1000000,输出13970034 发现还是超时
//n=100000,秒出，如何才能不超时？
//提交，果不其然Time_Limit_Exceed。2019-5-21
//以下为超时算法。2019-5-21  
//https://blog.csdn.net/aarongzk/article/details/50647495此文思路奇特，没有经过训练，确实难以想到，摘抄如下
//直接求每个数的因数个数是比较麻烦的，我们可以换一个角度考虑。
//对于每个数i，在1到n的范围内有多少个数是它的倍数？答案显然是n/i。于是最终的答案就是∑(n/i)。
//测试了n=1000000，真是秒出啊。
//样例通过，提交AC。2019-5-21
//以下为AC代码。
#include
#define LL long long
LL ans=0;
int main(){
    int n,i;
    scanf("%d",&n);
    for(i=1;i<=n;i++)ans+=n/i;
    printf("%lld\n",ans);
    return 0;
}

//1968: [Ahoi2005]COMMON 约数研究
//在线测评地址https://www.lydsy.com/JudgeOnline/problem.php?id=1968
//0 < N < 1000000要么O(logn)，要么O(nlogn)
//想到了 素数筛，想到了 约数成对出现 还想到了质因数分解6=2^1*3^1  约数个数(1+1)*(1+1)=4
//先写个素数筛 还不错，能独立写出。2019-5-21
//质数的约数为2，和数的约数分解质因数来处理
//2^20=1024*1024，故具体到某个数，阶数不超过20，故在筛的过程中，再计算 阶数 ,不超时，极限是20*10^6=2*10^7
//n=1无需特判，可读程序，即明白。
//测试了n=1000000,输出13970034，发现，还是要超时
//将以下两句进行优化
//for(j=1;j<=cnt;j++)
//    if(x%prime[j]==0)break;
//改成 while(x%prime[j])j++;
//测试了，n=1000000,输出13970034 发现还是超时
//n=100000,秒出，如何才能不超时？
//提交，果不其然Time_Limit_Exceed。2019-5-21
//以下为超时算法。2019-5-21  
#include
#include
#define LL long long
int prime[10000],not_prime[1000100],cnt=0;
LL sum=1;
int f(int x){//计算x的约数的个数
    int ans=1,c,j=1;
    while(x>1){
        c=1;
        while(x%prime[j])j++;
        while(x%prime[j]==0)c++,x/=prime[j];
        ans*=c;
    }
    return ans;
}
void linear_shaker(int n){
    int i,j;
    memset(not_prime,0,sizeof(not_prime));
    for(i=2;i<=n;i++){
        if(!not_prime[i])prime[++cnt]=i;
        for(j=1;prime[j]*i<=n;j++){//忘了加次层次的｛｝
            not_prime[prime[j]*i]=1;
            if(i%prime[j]==0)break;
        }
        if(!not_prime[i])sum+=2;//此处写成 if(not_prime[i])sum+=2;
        else sum+=f(i);//一开始将此if else 写到for(i=2循环之外了
    }
     
}
int main(){
    int i,n;
    scanf("%d",&n);
    linear_shaker(n);
    printf("%lld\n",sum);
    return 0;
}

3.bzoj 2761   //2761: [JLOI2011]不重复数字   //在线测评地址https://www.lydsy.com/JudgeOnline/problem.php?id=2761

//2761: [JLOI2011]不重复数字
//在线测评地址https://www.lydsy.com/JudgeOnline/problem.php?id=2761
//思路：结构体记录位置，值
//按值快排，
//结构题复制，去重
//按位置快排，输出结果
//样例通过，提交Wrong_Answer，真叫没想法。
//仔细想了想，快排是不稳定排序，问题强调"只保留第一次出现的数"
//马上对cmp1进行修改
//int cmp1(node a,node b){
//    return a.val //}
//改成
//int cmp1(node a,node b){
//    return a.val==b.val?a.pos //}
//提交，等了10分钟，AC了，没想到网站卡壳被我遇到了。
//快排是不稳定排序，这个坑不是第一次遇到了。2019-5-21
#include
#include
#include
#define maxn 50100
using namespace std;
struct node{
    int pos,val;
}a[maxn],b[maxn];
int cmp1(node a,node b){
    return a.val==b.val?a.pos }
int cmp2(node a,node b){
    return a.pos }
int main(){
    int T,n,i,cnt;
    scanf("%d",&T);
    while(T--){
        memset(a,0,sizeof(a)),memset(b,0,sizeof(b));
        scanf("%d",&n);
        for(i=1;i<=n;i++)scanf("%d",&a[i].val),a[i].pos=i;
        sort(a+1,a+1+n,cmp1);
        b[1]=a[1],cnt=1;
        for(i=2;i<=n;i++)
            if(a[i].val!=a[i-1].val)b[++cnt]=a[i];//去重
        sort(b+1,b+1+cnt,cmp2);
        printf("%d",b[1].val);
        for(i=2;i<=cnt;i++)printf(" %d",b[i].val);
        printf("\n");
    }
    return 0;
}

5.bzoj 1432   //1432: [ZJOI2009]Function   //在线测评地址https://www.lydsy.com/JudgeOnline/problem.php?id=1432

//1432: [ZJOI2009]Function
//在线测评地址https://www.lydsy.com/JudgeOnline/problem.php?id=1432
//直线两两相交，但没有三条直线交在一起，
//读题多遍，有疑问，分层的依据是什么，没弄明白啊
//题意理解很困难。2019-5-22
//经画图实践即观测不同图形形态，对题中的层作如下定义
//交点为层的边界，同一层，只能在交点的一侧，且两层之间的线段不能重合。

//https://blog.csdn.net/flaze_/article/details/52886497此文思路代码不错
//嗯………………考虑一下，显然可以上下翻转，于是对于求f[k]( k>(n/2))的，等效于求f[n-k]，所以只要保证对于某个n，前(n>>1)层的值最小即可
//考虑一下…………
//当n==1，答案是1
//当n==2，答案是2
//之后每次增加一条线，都不会影响前k层的值，但是因为题目说任意两条直线不平行，于是一定会有交点
//我们从上往下增加直线，当已经放了k-1条直线，在放第ｋ条直线的时候，
//如果直线k和直线k-1的交点在k-1原有交点的右边，坑定会影响前面的答案，不是最优，所以强行让交点在倒数第二个，不会影响f[k-1]，而f[k]显然会因此增加了2（自己画一画）

BZOJ刷题记录---普及组难度 AC_第2张图片

BZOJ刷题记录---普及组难度 AC_第3张图片

//n=1输出1
//n>1,有n层，若k<=n/2 输出2*k，反之输出(n-k+1)*2层
//说实话，该题，还是很难想出的。2019-5-22
//样例通过，提交AC。2019-5-22
#include
int main(){
    int n,k;
    scanf("%d%d",&n,&k);
    if(n==1)printf("1\n");
    else printf("%d\n",k<=n-k+1?2*k:(n-k+1)*2);
    return 0;
}

6.bzoj 3098   //3098: Hash Killer II   //在线测评地址https://www.lydsy.com/JudgeOnline/problem.php?id=3098 

//3098: Hash Killer II
//在线测评地址https://www.lydsy.com/JudgeOnline/problem.php?id=3098 
//如果一个房间里有23个或23个以上的人，那么至少有两个人的生日相同的概率要大于50%。
//https://baike.baidu.com/item/%E7%94%9F%E6%97%A5%E6%82%96%E8%AE%BA/2715290?fr=aladdin 
//生日悖论推导如下
#include
int main(){
    int i=1;
    double ans=1;//ans所有人生日都不相同的概率 
    while(1){
        ans*=(365-i+1)*1.0/365;
        if(ans<0.5)break;
        i++;
    }
    printf("i=%d ans=%lf\n",i,ans);
    return 0;
} 
//23的得出，可以看作是23=sqrt(365)
//https://www.cnblogs.com/wuminyan/p/5211715.html此文思路不错
//这里取模的数是10^9+7,所以只需要生成sqrt（10^9+7）≈100000的数就会出现冲突 
//提交AC。2019-5-22 22:07 

//此题关于l的取值，还是有些疑惑，日后要再看看。2019-5-22 22:16
#include
#include
int main(){
    int i;
    printf("100000 10\n");
    for(i=1;i<=100000;i++)printf("%c",rand()%26+'a');
    return 0;
} 

7.bzoj 1800   //1800: [Ahoi2009]fly 飞行棋   //在线测评地址https://www.lydsy.com/JudgeOnline/problem.php?id=1800

//1800: [Ahoi2009]fly 飞行棋
//在线测评地址https://www.lydsy.com/JudgeOnline/problem.php?id=1800
//画图进行研究，发现，只要知道 直径 数量m,C(m,2)即可得到长方形数量
//采用前缀和的方式，存储点间圆弧长度。
//若两点差值为圆周长一半，此两点即为直径。
//样例通过，提交Wrong_Answer，表示希望越大，失望越大。
//重读源代码，发现测试代码竟然没删除，if((sum[j]-sum[i])*2==sum[n])m++,printf("i=%d j=%d\n",i,j);
//天啊，功亏一篑，删除测试代码，提交AC.2019-5-23
//提交之前，还是要测试一遍，对对输出。
//该题独立完成，甚是欣慰。2019-5-23
//思维量比较大。
#include
int n,sum[25],m=0;
int main(){
    int i,j;
    scanf("%d",&n);
    sum[0]=0;
    for(i=1;i<=n;i++)scanf("%d",&sum[i]),sum[i]+=sum[i-1];//前缀和
    for(i=0;i         for(j=i+1;j             if((sum[j]-sum[i])*2==sum[n])m++;//统计直径 数量
    printf("%d\n",m*(m-1)/2);//任选2条直径。
    return 0;
}

8.bzoj 1218   //1218: [HNOI2003]激光炸弹   //在线测评地址https://www.lydsy.com/JudgeOnline/problem.php?id=1218
//读完题意，第一点，求子矩阵之和
//第二点，正方形占据的位置，可以是目标之间的空隙。
//考虑到数组计算问题，所有坐标值都自加1
//R=1,只能炸1个点
//R=2,只能炸(2-1)^2=1个点
//R=3,只能炸(3-1)^2=4个点
//R=4, 只能炸(4-1)^2=9个点
//故R=1时，使其变成R=2即可。
//样例通过，提交Wrong_Answer，信心慢慢，可惜。
//想了想，提供的数据很可能是长方形，而非正方形，故需补齐成正方形
//修改代码，提交Wrong_Answer
//发现
//for(i=R;i<=S;i++)//此处写成for(i=R;i<=row;i++)
//    for(j=R;j<=S;j++)//此处写成 for(j=R;j<=col;j++)
//修改，提交 Wrong_Answer
//在https://www.luogu.org/recordnew/show/19293278提交，30分，测试点1-2,6-10WA
//在洛谷里测试了一遍，发现是边界的问题。
//计算矩阵和的算法，没有问题。
//通过对比代码发先，题目叙述有问题，“若目标位于爆破正方形的边上，该目标将不会被摧毁。”
//还不如这样说R=1,有1个元素会被炸;R=2，有4个元素会被炸;R=3,有9个元素会被炸
//该题最后问题竟然出现在题意的理解问题上。2019-5-23 17:19
//在洛谷里提交通过，继续在bzoj上提交，AC。201-5-23 17:23
//该题的问题，题意不明，可惜，离成功只差一步，这一步，靠自己是难以 跨越的，还请出题人多多费心。

//做完该题，再做 bzoj 2462   //在线测评地址https://www.lydsy.com/JudgeOnline/problem.php?id=2462会更有收获

//bzoj 2462 题解  详见https://blog.csdn.net/mrcrack/article/details/90228821


#include
#include
int sum[5010][5010];//sum[i][j]表示[1][1]-[i][j]之间的矩阵和
int max(int a,int b){
    return a>b?a:b;
}
int main(){
    int i,j,n,R,row=0,col=0,x,y,v,ans=0,S=0;//此处写成 int i,j,n,R,row,col,x,y,v;
    memset(sum,0,sizeof(sum));
    scanf("%d%d",&n,&R);
    for(i=1;i<=n;i++)scanf("%d%d%d",&x,&y,&v),x++,y++,sum[x][y]=v,row=max(row,x),col=max(col,y);
    S=max(row,col);//漏考虑
    for(i=1;i<=S;i++)//此处写成 for(i=1;i<=row;i++)
        for(j=1;j<=S;j++)//此处写成 for(j=1;j<=col;j++)
            sum[i][j]+=sum[i][j-1];//行计算
    for(j=1;j<=S;j++)//此处写成 for(j=1;j<=col;j++)
        for(i=1;i<=S;i++)//此处写成 for(i=1;i<=row;i++)
            sum[i][j]+=sum[i-1][j];//列计算
    for(i=R;i<=S;i++)//此处写成for(i=R;i<=row;i++)
        for(j=R;j<=S;j++)//此处写成 for(j=R;j<=col;j++)
            ans=max(ans,sum[i][j]-sum[i][j-R]-sum[i-R][j]+sum[i-R][j-R]);
    printf("%d\n",ans);
    return 0;
}

9.bzoj 4001   //4001: [TJOI2015]概率论   //在线测评地址https://www.lydsy.com/JudgeOnline/problem.php?id=4001 

//4001: [TJOI2015]概率论
//在线测评地址https://www.lydsy.com/JudgeOnline/problem.php?id=4001 
//不得不说，树，确实是薄弱环节。 
//该题与二叉树的形态有关。 
//估计涉及 卡特兰数 
//看了 判断 树是否同构的代码，得出上述。 
//叶结点，有 2个极端，一是 链式，只有各一个叶结点
//另一个是 满二叉树，若达不到，接近满二叉树。对应最多节点.2019-5-23
//1<=N<=10^9，不用担心，因树中查找，算法的时间复杂度是O(logN) 
//回忆了 卡特兰数，还是想了起来，
//f(n)=f(n-1)f(0)+f(n-2)f(1)+f(n-3)f(2)+...+f(1)f(n-2)+f(0)f(n-1)
//根需占用1个节点，f(0)=1,f(1)=2
//期望的分母解决了，就是 卡特兰数
//分子 如何处理？
//大概就到这个程度了，准备开始翻看他人代码。
//翻看全网，发现思考方向正确，确实在分析 叶节点数量 需要学习 他人
//http://blog.miskcoo.com/2015/04/bzoj-4001?replytocom=44067此文思路不错
//卡特兰数 由 递推式 推导 公式，
//详见《数据结构(C语言版)》(严蔚敏 吴伟民）P152-P154 非常详细具体，超越网络中大部分的推导。

BZOJ刷题记录---普及组难度 AC_第4张图片

BZOJ刷题记录---普及组难度 AC_第5张图片

//学习上述几页内容的感慨，写书的作者在写书时，早已是熟练者的程度，

//书因篇幅的限制，在推导过程中，往往会略过作者认为的简单部分，

//但对于初学者来说，往往是难以逾越的障碍，很多初学者因此望而却步，

//能弄明白的，往往要花相当的精力及耐力。当然，就此也就相当部分被挡在了门外。2019-5-25 21:00

//找遍全网，从生成函数进行推导，也就此文写得好https://blog.csdn.net/Estia_/article/details/87915439摘抄如下

BZOJ刷题记录---普及组难度 AC_第6张图片

BZOJ刷题记录---普及组难度 AC_第7张图片

BZOJ刷题记录---普及组难度 AC_第8张图片

 

BZOJ刷题记录---普及组难度 AC_第9张图片

 

BZOJ刷题记录---普及组难度 AC_第10张图片

应该能比较容易的推导出(2n-2)!/(n-1)!/(n-1)!       2019-5-26 22:13

BZOJ刷题记录---普及组难度 AC_第11张图片

//2019-5-26 21:08

//提交AC。2019-5-26 22:18

#include

int main(){

    long long n;

    scanf("%lld",&n);

    printf("%.9lf\n",1.0*n*(n+1)/2/(2*n-1));

}

10.bzoj 2760   //2760: [JLOI2011]小A的烦恼   //在线测评地址https://www.lydsy.com/JudgeOnline/problem.php?id=2760

//2760: [JLOI2011]小A的烦恼
//在线测评地址https://www.lydsy.com/JudgeOnline/problem.php?id=2760
//","号数+1即为每行元素个数
//一个文件一个文件的处理
//开一个字符数组output[105][205*100],用来存储输出字符串
//每个文件处理时，每行都统计","的个数
//找出同个文件中最大","个数，其它行，不足","，补齐
//样例通过，提交Output_Limit_Exceed
//对比代码，发现网络中全是STL模版编写
//看完代码，觉得没有问题，突然想到，应是input初始化问题
//memset(input,0,sizeof(input)); //漏了此句，查了好久
//修改，提交AC。2019-5-27
#include
#include
char file[105],input[105][205],output[105][205*100];
int dot[105];
int max(int a,int b){
    return a>b?a:b;
}
int main(){
    int t,m,i,j,len,cnt,row=0;
    scanf("%d",&t);
    while(t--){
        memset(input,0,sizeof(input)); //漏了此句，查了好久
        memset(dot,0,sizeof(dot)),cnt=0;
        scanf("%d%s",&m,file);
        for(i=1;i<=m;i++){
            scanf("%s",input[i]);
            len=strlen(input[i]);
            for(j=0;j                 if(input[i][j]==',')
                    dot[i]++;
            cnt=max(cnt,dot[i]);//cnt用来统计当前文件最多","数
        }
        for(j=1;j<=cnt;j++)strcat(file,",");
        for(i=1;i<=100;i++){//此处写成 for(i=1;i<=m;i++)
            for(j=dot[i];j                 strcat(input[i],",");
        }
        if(t){//不是最后一个文件，补上文件间间隔","
            strcat(file,",");
            for(i=1;i<=100;i++)//此处写成 for(i=1;i<=m;i++)
                strcat(input[i],",");
        }
        strcat(output[0],file);
        for(i=1;i<=100;i++)strcat(output[i],input[i]);//此处写成 for(i=1;i<=m;i++)strcat(output[i],input[i]);
        row=max(row,m);
    }
    for(i=0;i<=row;i++)printf("%s\n",output[i]);
    return 0;
}

11.bzoj 1088   //1088: [SCOI2005]扫雷Mine   //在线测评地址https://www.lydsy.com/JudgeOnline/problem.php?id=1088

//1088: [SCOI2005]扫雷Mine
//在线测评地址https://www.lydsy.com/JudgeOnline/problem.php?id=1088
//题中少了图，建议可在https://www.luogu.org/problemnew/show/P2327看到缺失的图
//借助图形与样例，很快弄懂题意，不过，却没什么思路。
//有一点感觉，就是int可能溢出，采用long long稳妥
//此文思路代码都写得不错https://cloud.tencent.com/developer/article/1087793摘抄如下

BZOJ刷题记录---普及组难度 AC_第12张图片

//感叹，直接动手模拟，敢于尝试，这种能力还是比较欠缺。2019-5-27

//样例通过，提交AC。2019-5-27
#include
#define maxn 10010
int a[maxn],b[maxn];
int main(){
    int n,i,flag,cnt=0;
    scanf("%d",&n);
    a[0]=b[0]=0;//初始化
    for(i=1;i<=n;i++)scanf("%d",&b[i]);
    for(a[1]=0;a[1]<=1;a[1]++){//a[1]=0无雷，a[1]=1有雷
        flag=1;
        for(i=2;i<=n;i++){
            a[i]=b[i-1]-a[i-1]-a[i-2];//注b[i-1]=a[i-2]+a[i-1]+a[i]这样比较好理解
            if(!(a[i]==0||a[i]==1)){//即不是0，也不是1，即非法的情况
                flag=0;
                break;
            }
            if(i==n&&!(a[i]==b[i]-a[i-1]))flag=0;//边界还需判定
        }
        if(flag)cnt++;
    }
    printf("%d\n",cnt);
    return 0;
}

12.bzoj 1034   //1034: [ZJOI2008]泡泡堂BNB   //在线测评地址https://www.lydsy.com/JudgeOnline/problem.php?id=1034 

//1034: [ZJOI2008]泡泡堂BNB
//在线测评地址https://www.lydsy.com/JudgeOnline/problem.php?id=1034 
//田忌赛马 
//快排，升序，降序，进行比较 
//样例通过，提交Wrong_Answer。2019-5-27 21:05
//此文代码思路都很不错 https://blog.csdn.net/nike0good/article/details/8578176摘抄如下
//田忌赛马加强版。
//尽可能让最弱的赢，最强的赢，都不行则最弱打最强
//测试样例
//输入 
//4
//1 2 6 7
//1 2 4 7
//输出
//6 2 
//最差情况：
//容易发现2个队伍的总分一定(2-0,1-1,0-2)  即3场比分3:3，总得分6 2*n即是这样得出 
//所以ans2=2n-B队最高分
//样例通过，提交AC。2019-5-27 21:37
//重读了一遍田忌赛马的课文，发现课文上升不到算法高度。2019-5-27 21:40 
#include
#include
#define maxn 100100
using namespace std;
int a[maxn],b[maxn];
int cal(int *a,int *b,int n){
    int i=1,j=1,k=n,m=n,ans=0;
    while(i<=k){
        if(a[i]>b[j])ans+=2,i++,j++;
        else if(a[k]>b[m])ans+=2,k--,m--;
        else ans+=a[i]==b[m],i++,m--;
    }
    return ans;
}
int main(){
    int n,i,ans1,ans2;
    scanf("%d",&n);
    for(i=1;i<=n;i++)scanf("%d",&a[i]);
    for(i=1;i<=n;i++)scanf("%d",&b[i]);
    sort(a+1,a+1+n);
    sort(b+1,b+1+n);
    ans1=cal(a,b,n);
    ans2=2*n-cal(b,a,n);
    printf("%d %d\n",ans1,ans2);
    return 0;
}

13.bzoj 1207   //1207: [HNOI2004]打鼹鼠   //在线测评地址https://www.lydsy.com/JudgeOnline/problem.php?id=1207

//1207: [HNOI2004]打鼹鼠
//在线测评地址https://www.lydsy.com/JudgeOnline/problem.php?id=1207
//象数字三角形，但又不是
//f[t][x][y]动归，但发现n（n<=1000）, m（m<=10000），空间溢出
//此文思路不错https://www.cnblogs.com/five20/p/9021689.html摘抄如下
//本题吐槽数据太水，直接裸的最长上升子序列（O(n2)
//）也能过。。。
// 先贪心思路，由于给出的鼹鼠出现时间已经单调递增，所以一开始肯定是从第1
//个鼹鼠位置出发，因为就算从后面出发最多能到达的位置1都能到达。
//再考虑到从一个点到下一个点时间就是两点的曼哈顿距离，而且可以停留，
//那么限制条件就是abs(x[i]?x[j])+abs(y[i]?y[j])<=t[i]?t[j]。
// 此时容易想到本题实际在求类似最长上升子序列（只不过多了限制条件）。
// 所以定义状态f[i]
//表示前i个鼹鼠中最多打的鼹鼠个数，则不难想到状态转移方程：
//（前提：在满足限制条件下）f[i]=Max(f[j])+1,j∈[1,i)。
// 但是数据104
//，O(n2)显然超时（事实是数据太水～～直接过）。于是考虑优化，由于有限制条件，
//普通的二分优化就行不通了，此时一个贪心的玄学优化是设置一个mx[i]表示前i个数中最长上升子序列的长度，
//每次更新时同步更新mx，那么在限制条件前可以加一条可行性剪枝if(mx[j]+1<=f[i])break;
//（枚举j时倒序枚举，表示当前j个中的最长上升子序列长度+1都不大于f[i]，就没必要继续往前找了，因为往前长度显然会更小），
//每次更新mx也很简单：mx[i]=max(mx[i?1],f[i])。
// 最后输出目标状态ans
//就OK了。
//样例通过，提交AC。2019-5-28

//总体来讲，建模的能力还需加强。
#include
#define maxm 10010
int mx[maxm],t[maxm],x[maxm],y[maxm],f[maxm],ans;//mx[i] 1-i之间最大长度
int max(int a,int b){
    return a>b?a:b;
}
int abs(int a){
    if(a<0)a=-a;
    return a;
}
int main(){
    int n,m,i,j;
    scanf("%d%d",&n,&m);
    for(i=1;i<=m;i++)scanf("%d%d%d",&t[i],&x[i],&y[i]);
    mx[0]=0,ans=0;
    for(i=1;i<=m;i++){//最长上升子序列
        f[i]=1;
        for(j=i-1;j>=1;j--)//逆向查找
            if(mx[j]+1<=f[i])break;//剪枝
            else if(f[j]+1>f[i]&&abs(x[i]-x[j])+abs(y[i]-y[j])<=t[i]-t[j])
                f[i]=f[j]+1;
        mx[i]=max(f[i],mx[i-1]),ans=max(ans,f[i]);//写错位置，将其写在上面else if中
    }
    printf("%d\n",ans);
    return 0;
}

14.bzoj 2748   //2748: [HAOI2012]音量调节   //在线测评地址https://www.lydsy.com/JudgeOnline/problem.php?id=2748

//2748: [HAOI2012]音量调节
//在线测评地址https://www.lydsy.com/JudgeOnline/problem.php?id=2748
//改变音量，可加可减。50个点，2^50=1024^5超时
//深搜，剪枝，可以试试。
//过程中，若不在0-maxLevel范畴，则剪枝
//样例解释如下
//5-5+3+7=10
//样例通过，提交Time_Limit_Exceed
//深搜代码如下，虽然无法AC。2019-5-28
//此文思路代码都不错https://www.cnblogs.com/five20/p/9071611.html摘抄如下
//这是一次考试的防爆0的DP题目，5min钟就能刚完。
// 定义状态f[i][j]
//表示到了第j次操作，能否达到i的音量。初始状态f[st][0]=1
// 状态转移方程显而易见：if(f[i][j?1]==1)f[i+a[j]][j]=f[i?a[j]][j]=1
// 然后倒序找满足f[i][n]==1的最大的i。
//有01背包，布尔背包的味道
//样例通过，提交AC。2019-5-28
#include
#include
int c[1010],f[55][1010];
int main(){
    int i,j,n,b,m;
    scanf("%d%d%d",&n,&b,&m);
    for(i=1;i<=n;i++)scanf("%d",&c[i]);
    memset(f,0,sizeof(f)),f[0][b]=1;
    for(i=1;i<=n;i++)//第一重循环 是 个数
        for(j=0;j<=m;j++)
            if(f[i-1][j]){
                if(j-c[i]>=0)f[i][j-c[i]]=1;
                if(j+c[i]<=m)f[i][j+c[i]]=1;
            }
    for(j=m;j>=0;j--)
        if(f[n][j])break;
    printf("%d\n",j);//若不在0-m范围内，j=-1
    return 0;
}

//2748: [HAOI2012]音量调节
//在线测评地址https://www.lydsy.com/JudgeOnline/problem.php?id=2748
//改变音量，可加可减。50个点，2^50=1024^5超时
//深搜，剪枝，可以试试。
//过程中，若不在0-maxLevel范畴，则剪枝
//样例解释如下
//5-5+3+7=10
//样例通过，提交Time_Limit_Exceed
//深搜代码如下，虽然无法AC。2019-5-28
#include
int n,b,m,c[55],ans=-1;
int max(int a,int b){
    return a>b?a:b;
}
void dfs(int step,int level){
    if(level<0||level>m)return;
    if(step==n+1){
        ans=max(ans,level);
        return;
    }
    dfs(step+1,level+c[step+1]);
    dfs(step+1,level-c[step+1]);
}
int main(){
    int i;
    scanf("%d%d%d",&n,&b,&m);
    for(i=1;i<=n;i++)scanf("%d",&c[i]);
    dfs(0,b);
    printf("%d\n",ans);
    return 0;
}

15.bzoj 4302   //4302: Hdu 5301 Buildings   //在线测评地址https://www.lydsy.com/JudgeOnline/problem.php?id=4302

//4302: Hdu 5301 Buildings
//在线测评地址https://www.lydsy.com/JudgeOnline/problem.php?id=4302
//对了翻译，发现还是有些地方理解不到位。
//建议看看原题https://vjudge.net/problem/HDU-5301有配图对样例进行说明
//此文题意翻译不错https://blog.csdn.net/yeguxin/article/details/47029057 
//此文思路清晰https://blog.csdn.net/Fun_Zero/article/details/47059673摘抄如下

BZOJ刷题记录---普及组难度 AC_第13张图片

//此文https://blog.csdn.net/controlbear/article/details/52014702代码思路都写得很不错

//算法核心部分，用下图进行理解

BZOJ刷题记录---普及组难度 AC_第14张图片

//黑色为障碍，红色部分 (n+1)/2即可填充，白色部分 竖铺 max(up,down),横铺 max(left,right),之后在 竖铺 横铺 中选取最小值

//最后，在红色填充，与白色 铺中选取最大值。2019-6-1 8:39

//思路如上图
//样例通过，提交Wrong_Answer 
//重读代码，发现 right=m-y+1;//此处写成 right=n-y+1 笔误
//修改，提交Wrong_Answer 
//left=y//此处写成left=y+1对比代码，才发现
//修改，提交AC。2019-6-1 9:02
//想到与做到，还是有一定距离。 
#include
void swap(int *a,int *b){
    int t;
    t=*a,*a=*b,*b=t;
}
int min(int a,int b){
    return a }
int max(int a,int b){
    return a>b?a:b;
}
int main(){
    int n,m,x,y,up,down,left,right,ans,h,w,white;
    while(scanf("%d%d%d%d",&n,&m,&x,&y)!=EOF){
        if(n>m)swap(&n,&m),swap(&x,&y);
        ans=(n+1)/2;
        if(n==m&&n%2&&x==y&&x==(n+1)/2)ans--;//特判
        else{
            up=x-1,down=n-x,left=y,right=m-y+1;//此处写成left=y+1对比代码，才发现//此处写成 right=n-y+1 笔误 
            h=max(up,down),w=min(left,right),white=min(h,w);//白色区域处理 
            ans=max(white,ans);//白红区域合并 
        } 
        printf("%d\n",ans);
    }
    return 0;
}

16.bzoj 1083   //1083: [SCOI2005]繁忙的都市   //在线测评地址https://www.lydsy.com/JudgeOnline/problem.php?id=1083

//1083: [SCOI2005]繁忙的都市
//在线测评地址https://www.lydsy.com/JudgeOnline/problem.php?id=1083
//该题就是一个裸的最小生成树
//准备采用Kruskal算法，因其简单好写。
//样例通过，提交AC。2019-6-1 20:57
#include
#include
using namespace std;
int n,m,f[306];
struct node{
    int u,v,c;
}e[306*306/2];
int cmp(node a,node b){
    return a.c }
int getf(int u){
    return f[u]==u?u:f[u]=getf(f[u]);
}
int merge(int u,int v){
    int f1=getf(u),f2=getf(v);
    if(f1!=f2){
        f[f2]=f1;//左靠
        return 1;
    }
    return 0;
}
int main(){
    int i,u,v,c,b=0;
    scanf("%d%d",&n,&m);
    for(i=1;i<=n;i++)f[i]=i;
    for(i=1;i<=m;i++)scanf("%d%d%d",&e[i].u,&e[i].v,&e[i].c);
    sort(e+1,e+1+m,cmp);
    for(i=1;i<=m;i++)
        if(merge(e[i].u,e[i].v)){
            b++;
            if(b==n-1){
                printf("%d %d\n",n-1,e[i].c);
                break;
            }
        }
    return 0;
}

17.bzoj 2563   //2563: 阿狸和桃子的游戏   //在线测评地址https://www.lydsy.com/JudgeOnline/problem.php?id=2563

//2563: 阿狸和桃子的游戏
//在线测评地址https://www.lydsy.com/JudgeOnline/problem.php?id=2563
//最有策略，包括互相干扰吗，尝试了一下，没有对上样例，搜索网络，发现想不到，或者说不会想
//https://www.cnblogs.com/zzyh/p/7640470.html此文思路摘抄如下
//把一条边的边权分给两端的点权，如果一条边的两端被两人选择，那么最后得分相减时会抵消，如果被一个人选择，那么
//这条边的权值都会给他。
//100000/2*10000=5*10^8 int不会溢出
//因权值可能为奇数，故将其扩大1倍，最后处理完后，再将结果除2.   疑虑，除2前 可能为奇数
//样例通过，提交AC。2019-6-2 8:36
#include
#include
using namespace std;
int v[10010];
int cmp(int a,int b){
    return a>b;
}
int main(){
    int n,m,a,b,c,i,sum1=0,sum2=0;
    scanf("%d%d",&n,&m);
    for(i=1;i<=n;i++)scanf("%d",&v[i]),v[i]*=2;
    for(i=1;i<=m;i++)scanf("%d%d%d",&a,&b,&c),v[a]+=c,v[b]+=c;
    sort(v+1,v+1+n,cmp);
    for(i=1;i<=n;i++)
        if(i%2)sum1+=v[i];
        else sum2+=v[i];
    printf("%d\n",(sum1-sum2)/2);
    return 0;
}

18.bzoj 3097   //3097: Hash Killer I   //在线测评地址https://www.lydsy.com/JudgeOnline/problem.php?id=3097

//3097: Hash Killer I
//在线测评地址https://www.lydsy.com/JudgeOnline/problem.php?id=3097
//第二次遇到该题，这次终于看懂了题干中的代码。觉得写得不错，没什么问题。
//怎么卡，在没有提示的情况下，没有思路。
//打算测试unsigned long long自然溢出，操作系统中的计算器，支持不好
//马上降维，测试unsigned int自然溢出.2019-6-2 15:05
//自然溢出代码如下 
#include
int main(){
    unsigned int x;
    while(scanf("%u",&x)!=EOF) printf("%u\n",x);
    return 0;
}
//win7测试效果如下
4294967295
4294967295
4294967296
0
4294967297
1
4294967298
2
//自然溢出相当于 模  4294967296即2^32 那么 unsigned long long溢出同理。2019-6-2 15:22 

//Ubuntu14.04.2 采用 g++ 3097.cpp -o 3097
//  ./3097测试效果如下
-1
4294967295
4294967295
4294967295
4294967296
4294967295
4294967297
4294967295
4294967298
4294967295
//对上述结果深表遗憾，在Ubuntu14.04.2 采用 g++ 3097.cpp -o 3097 自然溢出是什么情况？2019-6-2 15:29

//https://blog.csdn.net/regina8023/article/details/43112899此文思路写得不错，摘抄如下
非常神奇的构造题。
首先明白两点：
1.卡hash的关键在于构造两个不同的串对应的hash值相同。
2.爆u64相当于对2^64这个数取模。
如果base是偶数，那么a.........aaa(>64个a)与ba.......aa(a的数量为前面那么串a的数量-1)，这两个串长度相同，hash值相同，显然串是不同的，这样就卡掉了。(通篇看完后，才弄懂此处，ba.......aa中 (‘b’-'a')*base^(前面那么串a的数量-1)  因 base是偶数，故  2^64\(‘b’-'a')*base^(串a的数量-1) mrcrack添加 2019-6-2 22:14 )
如果base是奇数，就比较麻烦了。
看vfk的做法吧：
如果base是奇数的话，现在只考虑a、b两个字母。
a \ b表示a能整除b。（orz 具体数学）
设数学上的函数not(S)表示把字符串S中每个位置的'a'变成'b'，把'b'变成'a'后形成的字符串。比如not("ababaa") = "bababb"
strA . strB代表字符串串联。如"娃" . "哈哈" = "娃哈哈"
|str|表示字符串str的长度。
设字符串序列{orzstr[i]}，orzstr[1] = "a", orzstr[i] = orzstr[i - 1] . not(orzstr[i - 1]) （注，i>=2 mrcrack添加）
那么|orzstr[i]| = |orzstr[i - 1]| * 2。显然这是等比数列，得到：|orzstr[i]| = |orzstr[1]| . 2 ^ (i - 1) = 2 ^ (i - 1)
设hash(str)为str的哈希值。
则：
hash(orzstr[i]) = hash(orzstr[i - 1]) * base ^ |not(orzstr[i - 1])| + hash(not(orzstr[i - 1]))   (由题干中 hash算法决定 mrcrack添加)
                       = hash(orzstr[i - 1]) * base ^ (2 ^ (i - 2)) + hash(not(orzstr[i - 1]))
hash(not(orzstr[i])) = hash(not(orzstr[i - 1])) * base ^ (2 ^ (i - 2)) + hash(orzstr[i - 1])   (对比上式，依次类推 mrcrack添加)
两式相减：
   hash(orzstr[i]) - hash(not(orzstr[i]))
= (hash(orzstr[i - 1]) * base ^ (2 ^ (i - 2)) + hash(not(orzstr[i - 1]))) - (hash(not(orzstr[i - 1])) * base ^ (2 ^ (i - 2)) + hash(orzstr[i - 1]))
= (hash(orzstr[i - 1]) - hash(not(orzstr[i - 1]))) * (base ^ (2 ^ (i - 2)) - 1)
这让我们发现，hash(orzstr[i]) - hash(not(orzstr[i]))似乎是个神奇的东西。而我们的目的实际上是要找两个字符串strA, strB使得
hash(strA) % 2^64 = hash(strB) % 2^64
相当与
2^64 \ hash(strA) - hash(strB)
设数列{f[i]}，f[i] = hash(orzstr[i]) - hash(not(orzstr[i]))
这样就有：
f[i] = f[i - 1] * (base ^ (2 ^ (i - 2)) - 1)
还是有点不爽啊……我们再设数列{g[i]}，g[i] = base ^ (2 ^ (i - 1)) - 1
于是能写成：
f[i] = f[i - 1] * g[i - 1]
则f[i] = f[1] * g[1] * g[2] * ... * g[i - 1]
然后发现一个神奇的事情？
base是奇数，则base的任意正整数次方也一定是奇数。所以对于任意的i必有g[i]为偶数，所以2 ^ (i - 1) \ f[i]  （即 g[1]=2*k1,g[2]=2*k2,g[3]=2*k3,...,g[i-1]=2*k(i-1),故2^(i-1)\g[1]*g[2]*...*g[i-1] mrcrack添加 2019-6-2 21:54）
问题是不是结束了呢……发现没有……这样的话我们要使2 ^ 64 \ f[i]，至少得让i = 65……然后发现|orzstr[65]|是个天文数字。
发现我们刚才那样分析太坑爹了……
i > 1时有：
g[i] = base ^ (2 ^ (i - 1)) - 1 = (base ^ (2 ^ (i - 2)) - 1) * (base ^ (2 ^ (i - 2)) + 1) = g[i - 1] * 一个偶数
而g[1]显然是偶数吧……
那么4 \ g[2]，8 \ g[3]...
也就是说2 ^ i \ g[i]
所以f[i] 实际上有：
(2 ^ 1) * (2 ^ 2) * (2 ^ 3) * ... * (2 ^ (i - 1)) \ f[i]
2 ^ (i * (i - 1) / 2) \ f[i]
当i取12时，就有66个2了哟！
这就是卡base为奇数时的方法。orzstr[12]和not(orzstr[12])即为所求。
而读入中base既有奇数又有偶数，直接在奇数构造的字符串后面加64个a就可以了。
//感觉该题，属于 出题人 自娱自乐，这种构造怎么想得到。2019-6-2 21:12
//不过，通过该问题学习，对hash的冲突，有了更深刻的了解。

//比较奇怪，该题的输出数据是怎么个形式，因为存在多解。2019-6-3 5:51

//样例通过，提交AC。2019-6-3 8:56
#include
int str[(1<<12)+65+10];
int main(){
    int n,L,i,j,now=1;
    printf("%d %d\n",(1<<12)+65,1<<11);//每串 orzstr[12]和not(orzstr[12] 即1<<11,两串拼接,即1<<12,65由来 b+65个a 串中 取b+64个a 和 65个a
    str[1]='a';
    for(i=1;i<=12;i++){
        for(j=1;j<=now;j++)
            str[now+j]=str[j]=='a'?'b':'a';
        now*=2;
    }
    for(i=1;i<=(1<<12);i++)printf("%c",str[i]);//打印两串完全相反的串组成的新串。 对应base 为 奇数
    for(i=1;i<=65;i++)printf("a");//打印附加的65个a 对应 base 为 偶数
    return 0;
}

19.bzoj 1022 //1022: [SHOI2008]小约翰的游戏John   //在线测评地址https://www.lydsy.com/JudgeOnline/problem.php?id=1022

//1022: [SHOI2008]小约翰的游戏John
//在线测评地址https://www.lydsy.com/JudgeOnline/problem.php?id=1022
//https://blog.csdn.net/mrcrack/article/details/80562324通过此文学习 Nim游戏 弄明白了 原理
//该题数据，均化成二进制，奇数个1,后手赢，偶数个1,先手赢。
//判断 奇数个1 偶数个1 异或 最合适。
//写着写着，还是觉得上述思路有误，因结果与Nim刚好相反，故思路还是要有大动。2019-6-3 22:16
//分类讨论。此文思路写得不错https://blog.csdn.net/clover_hxy/article/details/53818624

//搜遍网络，速成解析均难以理解，无奈，只好从头开始研习国家集训队的3篇论文。

//https://wenku.baidu.com/view/e119050a326c1eb91a37f111f18583d049640fe2.html?from=search《由感性认识到理性认识——透析一类搏弈游戏的解答过程》2019-6-3 21:38

上文中 若A胜B胜，则有时S胜，有时S负。感到难以理解，A胜，之后B开始时，乙先手，在B中，乙胜，即S负。2019-6-3 22:07

//https://wenku.baidu.com/view/67e4e88583d049649b6658f0.html《解析一类组合游戏》

//https://wenku.baidu.com/view/7cd481e9524de518964b7d1f.html《组合游戏略述——浅谈SG游戏的若干拓展及变形》

//https://blog.csdn.net/bestsort/article/details/88197959SG函数此文介绍得不错 2019-6-6 22:40

//https://blog.csdn.net/strangedbly/article/details/51137432SG函数此文图文并貌。2019-6-7 22:00
摘自https://blog.csdn.net/PoPoQQQ/article/details/40543799

题目大意：反Nim游戏，即取走最后一个的人输

首先状态1：如果所有的堆都是1，那么堆数为偶先手必胜，否则先手必败

然后状态2：如果有两个堆数量相同且不为1，那么后手拥有控场能力，即：

若先手拿走一堆，那么后手可以选择将另一堆留下1个或者全拿走，使这两堆最终只剩1个或0个；

若先手将一堆拿剩一个，那么后手可以选择将另一堆留下一个让先手拿或全拿走，使这两堆最终只剩1个或0个；

若先手将一堆拿走一部分，那么后手可以将另一堆同样拿走一部分，然后同上

状态3：若Xor!=0 那么先手可以先拿走一部分让Xor=0 然后同状态2先手必胜 否则先手必败

※鉴于本人过于沙茶，以上内容仅存在参考价值，无法证明正确性，欢迎指正

于是若所有堆全是1 Xor==0先手必胜 否则后手必胜

若有堆不是1 Xor==0后手必胜 否则先手必胜
摘自https://blog.csdn.net/WerKeyTom_FTD/article/details/48207079

Anti-SG游戏定义

1、决策集合为空的操作者胜。
2、其余规则与SG游戏一致。
SJ定理

对于任意一个Anti-SG游戏，如果定义所有子游戏的SG值为0时游戏结束，先手必胜的条件：
1、游戏的SG值为0且所有子游戏SG值均不超过1。
2、游戏的SG值不为0且至少一个子游戏SG值超过1。
证明

先证明第一个条件：
所有都不超过1，那么显然如果有偶数个1则先手必胜偶数个1即游戏的SG值为0。

再证明第二个条件：

如果有至少两个子游戏SG值超过1，然后其余有偶数个1。那么游戏的SG值就为所有SG值超过1的子游戏的SG值的Nim和。设为X。假设X中1的最高位为第k位，那么一定存在至少一个子游戏的SG值第k位有1，设这个子游戏的SG值为Y。那么我们可以把这个子游戏变为YxorX
。可以知道YxorX

。接下来游戏的SG值便变为0，而此时至少存在一个子游戏的SG值超过1。此条件下先手必胜。

如果有至少两个子游戏的SG值超过1，然后其余有奇数个1。我们设所有SG值超过1的子游戏的SG值的Nim和为X。那么游戏的SG值为Xxor1

。因为不为0，那么现在如果X=0，我们去掉一个1即可。于是变为游戏的SG值为0，而此时至少存在两个子游戏的SG值超过1。如果X不为0，那么最高位的1一定不在第一位。于是和1没有关系，像上面一样处理即可。

如果只有一个子游戏的SG值超过1，然后其余有偶数个1。显然我们可以拿将那个超过1的子游戏转移到一个决策使SG值为1，就能造成奇数个1。

如果只有一个子游戏的SG值超过1，然后其余有奇数个1。直接将那个超过1的子游戏转移到一个决策使SG值为0，就能造成奇数个1。

这样证明了先手必胜局面有至少一个后继局面为先手必败局面。
接下来需证明每一个先手必败局面都只能转移到先手必胜局面。
先来证明第二个条件：
所有SG值不超过1，那么有奇数个1先手就必败，无论如何都只能转移到有偶数个1的情况。有奇数个1即游戏的SG值不为0。

第一个条件：
如果有至少两个子游戏的SG值超过1，那么无论如何都会转移到一个先手必胜局面（有至少一个SG值超过1，游戏的SG值不为0），因为无法造成游戏的SG值继续为0。

如果只有一个子游戏的SG值超过1，这是不可能发生的，不可能存在一个局面只有一个子游戏SG值超过1但异或和为0的，一定有至少两个子游戏SG值超过1。

证毕。

//样例通过，提交AC.2019-8-4 17:59

#include
int main(){
    int t,n,x,ans,flag;
    scanf("%d",&t);
    while(t--){
        ans=0,flag=0;
        scanf("%d",&n);
        while(n--){
            scanf("%d",&x);
            ans^=x;
            if(x>1)flag=1;
        }
        if(ans==0&&flag==0)printf("John\n");
        else if(ans&&flag)printf("John\n");
        else printf("Brother\n");
    }
    return 0;
}

 

20.bzoj 2465   //2465: [中山市选2009]小球   //在线测评地址https://www.lydsy.com/JudgeOnline/problem.php?id=2465

//2465: [中山市选2009]小球
//在线测评地址https://www.lydsy.com/JudgeOnline/problem.php?id=2465
//准备上背包，再次读题，发现没这么复杂
//快排，自大到小，再进行选择
//前缀和，能快速计算，马上加上该功能。
//样例通过，提交Wrong_Answer
//这么简单的题，怎么可能。2019-6-5
//重新读题，发现误解提议，原以为是球装最多球的瓶 及其 分数
//读完题目，发现是用上所有瓶子，装的球数，以及分数。
//样例通过，提交Wrong_Answer。2019-6-5 19:25
//重读代码，发现if(j==m+1)break;//此处写成if(j==n+1)break;昏招
//修改，提交Wrong_Answer
//对比他人代码，发现思路没有问题
//看了数据范围，0 <= c <= 200，没想到c可以等于0,这点没考虑到,在读取数据时，马上将该组数据丢弃
//又看了数据范围，0<=m<=200，发现m可以等于0,马上进行特判。
//提交Wrong_Answer，2019-6-5 21:16
//while(scanf("%d%d",&n,&m)&&(n!=0||m!=0)){//此处写成while(scanf("%d%d",&n,&m)&&!(n==0&&m==0))
//修改，提交Wrong_Answer
//https://blog.csdn.net/Mmh2000/article/details/76599914翻到这里才发现，是if与while的问题
//决定重写代码,样例通过，提交AC。
//该题最大的难点，在于c可以等于0,并且可以有一串的c等于0.
#include
#include
#include
using namespace std;
int a[210];
struct node{
    int c,q;
}b[210];
int cmp(int a,int b){
    return a>b;
}
int cmp2(node a,node b){
    return a.q>b.q;
}
int main(){
    int n,m,i,j,ans1,ans2;
    while(scanf("%d%d",&n,&m)&&n&&m){
        for(i=1;i<=n;i++)scanf("%d",&a[i]);
        sort(a+1,a+1+n,cmp);
        for(i=1;i<=m;i++) scanf("%d%d",&b[i].c,&b[i].q);
    sort(b+1,b+1+m,cmp2);
        ans1=ans2=0,i=1,j=1;
        while(i<=n){
            while(!b[j].c){//此处是难点，写成if错，写成while对。2019-6-5 22:30
                j++;
                if(j==m+1)break;
        }
        if(b[j].q>=a[i])ans1++,ans2+=a[i],b[j].c--;
        i++;//漏了此句
    }
        printf("%d %d\n",ans1,ans2);
    }
    return 0;
}

//2465: [中山市选2009]小球
//在线测评地址https://www.lydsy.com/JudgeOnline/problem.php?id=2465
//准备上背包，再次读题，发现没这么复杂
//快排，自大到小，再进行选择
//前缀和，能快速计算，马上加上该功能。
//样例通过，提交Wrong_Answer
//这么简单的题，怎么可能。2019-6-5
//重新读题，发现误解提议，原以为是球装最多球的瓶 及其 分数
//读完题目，发现是用上所有瓶子，装的球数，以及分数。
//样例通过，提交Wrong_Answer。2019-6-5 19:25
//重读代码，发现if(j==m+1)break;//此处写成if(j==n+1)break;昏招
//修改，提交Wrong_Answer
//对比他人代码，发现思路没有问题
//看了数据范围，0 <= c <= 200，没想到c可以等于0,这点没考虑到,在读取数据时，马上将该组数据丢弃
//又看了数据范围，0<=m<=200，发现m可以等于0,马上进行特判。
//提交Wrong_Answer，2019-6-5 21:16
//while(scanf("%d%d",&n,&m)&&(n!=0||m!=0)){//此处写成while(scanf("%d%d",&n,&m)&&!(n==0&&m==0))
//修改，提交Wrong_Answer
//https://blog.csdn.net/Mmh2000/article/details/76599914翻到这里才发现，是if与while的问题
//经过一番修改，自己的代码也AC了。2019-6-5 22:44
#include
#include
#include
using namespace std;
int a[210];
struct node{
    int c,q;
}b[210];
int cmp(int a,int b){
    return a>b;
}
int cmp2(node a,node b){
    return a.q>b.q;
}
int main(){
    int n,m,i,j,ans1,ans2,c,q;
    while(scanf("%d%d",&n,&m)&&n&&m){
        for(i=1;i<=n;i++)scanf("%d",&a[i]);
        sort(a+1,a+1+n,cmp);
        j=0;
        for(i=1;i<=m;i++){
            scanf("%d%d",&c,&q);
            if(c>0)j++,b[j].c=c,b[j].q=q;
        }
        m=j;
        if(m==0){//特判
            printf("0 0\n");
            continue;
        }
    sort(b+1,b+1+m,cmp2);
        ans1=ans2=0,i=1,j=1;
        while(i<=n){
            if(a[i]<=b[j].q){
                ans1++,b[j].c--,ans2+=a[i];
                if(b[j].c==0){//此处写成if(b[j].c==0)
                    j++;
                    if(j==m+1)break;//此处写成if(j==n+1)break;昏招
                }
        }
        i++;//漏了此句
    }
        printf("%d %d\n",ans1,ans2);
    }
    return 0;
}

21.bzoj 2122   //2122: 工作评估   //在线测评地址https://www.lydsy.com/JudgeOnline/problem.php?id=2122

//2122: 工作评估
//在线测评地址https://www.lydsy.com/JudgeOnline/problem.php?id=2122
//啥算吗，估计要超时
//计算50000*50000=2.5*10^9超时无疑。
//样例通过，提交Time_Limit_Exceed
//以下为超时代码。2019-6-6
//以下为卡时间，恰好AC代码，发现减少变量，也能缩减一点点时间，分块算法 等百题之后再来吧。2019-6-6
//此文值得一看https://blog.csdn.net/qq_36797743/article/details/74626217
#include
#define maxn 50010
int D[maxn],L[maxn];
int min(int a,int b){
    return a }
int max(int a,int b){
    return a>b?a:b;
}
int main(){
    int n,m,i,left,right,ans,X0,X;
    scanf("%d%d",&n,&m);
    for(i=1;i<=n;i++)scanf("%d",&D[i]);
    for(i=1;i<=n;i++)scanf("%d",&L[i]);
    while(m--){
        scanf("%d%d%d",&left,&right,&X0);
        ans=0,X=X0;
        for(i=left;i<=right;i++)X=min(X+D[i],L[i]),X=max(X,X0),ans=max(X,ans);//此处写成 for(i=left;i<=right;i++)X[i]=X[i-1]+D[i],X[i]=min(X[i],L[i]),X[i]=max(X[i],X[0]),ans=max(X[i],ans);
        printf("%d\n",ans);
    }
    return 0;
}

//2122: 工作评估
//在线测评地址https://www.lydsy.com/JudgeOnline/problem.php?id=2122
//啥算吗，估计要超时
//计算50000*50000=2.5*10^9超时无疑。
//样例通过，提交Time_Limit_Exceed
//以下为超时代码。2019-6-6
//
#include
#define maxn 50010
int D[maxn],L[maxn],X[maxn];
int min(int a,int b){
    return a }
int max(int a,int b){
    return a>b?a:b;
}
int main(){
    int n,m,i,j,left,right,ans;
    scanf("%d%d",&n,&m);
    for(i=1;i<=n;i++)scanf("%d",&D[i]);
    for(i=1;i<=n;i++)scanf("%d",&L[i]);
    while(m--){
        ans=0;
        scanf("%d%d%d",&left,&right,&X[0]);
        X[left-1]=X[0];//初始化,该句比较关键
        for(i=left;i<=right;i++)X[i]=X[i-1]+D[i],X[i]=min(X[i],L[i]),X[i]=max(X[i],X[0]),ans=max(X[i],ans);
        printf("%d\n",ans);
    }
    return 0;
}
 

22.bzoj 1197   //1197: [HNOI2006]花仙子的魔法   //在线测评地址https://www.lydsy.com/JudgeOnline/problem.php?id=1197

//1197: [HNOI2006]花仙子的魔法
//在线测评地址https://www.lydsy.com/JudgeOnline/problem.php?id=1197
//对样例表示奇怪，不是000,001,010,011,100,101,110,111,共计8种吗
//输出结果，如何跟n维扯上关系。
//看了https://www.luogu.org/problemnew/solution/P4176中的图，对样例有了点感觉
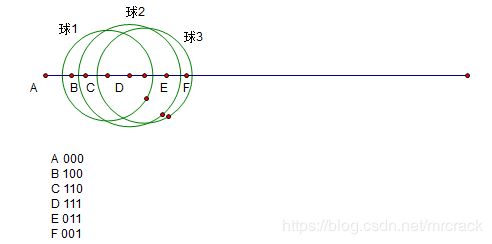
//尝试画图(如下)，弄明白了样例，可喜可贺。2019-6-8 20:56

BZOJ刷题记录---普及组难度 AC_第15张图片

//想了想，m次魔法，极限类型为2^m次。
//弄懂题意，但是该题难想。
//https://blog.csdn.net/sunshinezff/article/details/48134717此文思路不错，摘抄如下
//简化一下这个题就是让你求一个n维的类似球一样的东西能把一个n维的空间最多分成几个部分。
//然后我们考虑最后一个球。
//两个n维物体的交一定是一个n-1维物体。第m个球最多能和m-1个球相交。这就相当于用m个n-1维的物体去划分一个n-1
//维空间。显然这个之前已经算出来了。
//设 f[i][j]为用j个i维物体去划分一个i维空间，可以划分成最多几个部分。
//所以dp方程就是 f[i][j]=f[i-1][j]+f[i-1][j-1];
//https://www.cnblogs.com/VisJiao/p/BZOJ1197.html此文边界写得不错，推导也值得一看
//记录ans[k][i]表示k维空间中的i个球最多将空间划分为几部分。
//一维情况非常简单，ans[1][i]=2i。一维上的球就是两个点。
//接下来考虑二维情况。假设现在有x个圆，要加入一个新圆。这个新圆可以与之前的每个圆相交，共有2x个交点，圆弧被分成2x份。
//这2x个圆弧都将其所在部分一分为二，也就增加了2x个部分。ans[2][i]=i2−i+2。
//然后考虑三维情况。现在有x个球，要加入一个新球。这个新球可以与之前的每个球相交，每两个球会交出一个圆，那么新球
//的球面就被x个圆划分成ans[2][x]个曲面。这ans[2][x]个曲面都将其所在部分一分为二，
//也就增加了ans[2][x]个部分。ans[3][x+1]=ans[3][x]+ans[2][x]。
//...于是我们发现了一些规律。一个k维球会与i个k维球交出i个k−1维球，
//会增加ans[k−1][i]个部分，即ans[k][i+1]=ans[k][i]+ans[k−1][i]。有初值ans[k][0]=1，那么我们可以递推得到ans[n][m]。
//思维要求高，比较难想到
//样例通过，提交Wrong_Answer
//一查，for(i=1;i<=m;i++)f[1][i]=2*i;//此处写成for(i=1;i<=m;i++)f[1][i]=2*m;
//提交AC。2019-6-8 23:38
#include
#define LL long long
LL f[20][105];
int main(){
    int n,m,i,j;
    scanf("%d%d",&m,&n);//此处写成scanf("%d%d",&n,&m);
    for(i=1;i<=n;i++)f[i][0]=1;//0次魔法，对应值为1
    for(i=1;i<=m;i++)f[1][i]=2*i;//此处写成for(i=1;i<=m;i++)f[1][i]=2*m;//1维空间，对应花的种类
    for(i=2;i<=n;i++)
        for(j=1;j<=m;j++)
            f[i][j]=f[i][j-1]+f[i-1][j-1];
    printf("%lld\n",f[n][m]);
    return 0;
}

23.bzoj 1295   //1295: [SCOI2009]最长距离   //在线测评地址https://www.lydsy.com/JudgeOnline/problem.php?id=1295

//1295: [SCOI2009]最长距离
//在线测评地址https://www.lydsy.com/JudgeOnline/problem.php?id=1295
//通过样例1弄懂题意,最远距离为sqrt(2)，求最远的两点之间的直线距离，看了数据范围，20分容易得。
//通过样例3弄懂了，取出1个障碍的情况，将右下角的1去除，最远距离为2×sqrt(2)
//样例2,最远距离为sqrt(2^2+3^2)
//题意明白后，怎么算。没所有思路
//此文思路写得不错https://www.cnblogs.com/mjtcn/p/8866936.html摘抄如下
//每次选两个点，spfa，到每个点需要搬多少石头，再枚举两个点，
//判断是否可以在搬得石头的个数小于t的情况下，走到，取最大值。
//此文代码写得不错，值得一读http://hzwer.com/1318.html
//spfa
//h=t=1,q[t].r=rr,q[t].c=cc,t++,vis[rr][cc]=1,dis[rr][cc]=map[rr][cc];//漏了此句dis[rr][cc]=map[rr][cc]
//if(dis[i][j]<=T){//此处写成if(dis[rr][cc]<=T)
//样例通过，提交AC。2019-6-9 21:07  
#include
#include
#include
#define maxn 33
int map[maxn][maxn],dis[maxn][maxn],n,m,T,vis[maxn][maxn],ans=0;
int next[][2]={{-1,0},{1,0},{0,-1},{0,1}};//上 下 左 右
char str[maxn];
struct node{
    int r,c;
}q[maxn*maxn*100];
void getans(int rr,int cc){
    int i,j,t;
    for(i=rr;i<=n;i++)
        for(j=1;j<=m;j++)//此处写成for(j=1;j<=n;j++)
            if(dis[i][j]<=T){//此处写成if(dis[rr][cc]<=T)
                t=(rr-i)*(rr-i)+(cc-j)*(cc-j);
                if(t>ans)ans=t;
            }
}
void spfa(int rr,int cc){
    int h,t,nowr,nowc,nr,nc,k;
    memset(vis,0,sizeof(vis)),memset(dis,127,sizeof(dis));
    h=t=1,q[t].r=rr,q[t].c=cc,t++,vis[rr][cc]=1,dis[rr][cc]=map[rr][cc];//漏了此句dis[rr][cc]=map[rr][cc]
    while(h         nowr=q[h].r,nowc=q[h].c;
        for(k=0;k<4;k++){
            nr=nowr+next[k][0],nc=nowc+next[k][1];
            if(1<=nr&&nr<=n&&1<=nc&&nc<=m&&dis[nowr][nowc]+map[nr][nc]                 dis[nr][nc]=dis[nowr][nowc]+map[nr][nc];
                if(!vis[nr][nc])vis[nr][nc]=1,q[t].r=nr,q[t].c=nc,t++;
            }
        }
        vis[nowr][nowc]=0;
        h++;
    }
    getans(rr,cc);
}
int main(){
    int i,j;
    scanf("%d%d%d",&n,&m,&T);
    for(i=1;i<=n;i++){
        scanf("%s",str+1);
        for(j=1;j<=m;j++)map[i][j]=str[j]-'0';
    }
    for(i=1;i<=n;i++)
        for(j=1;j<=m;j++)
            spfa(i,j);
    printf("%.6lf\n",sqrt(1.0*ans));//此处写成printf(".6lf\n",sqrt(1.0*ans));竟然半天没看出来
    return 0;
}

24.bzoj 1821   //1821: [JSOI2010]Group 部落划分 Group   //在线测评地址https://www.lydsy.com/JudgeOnline/problem.php?id=1821

//1821: [JSOI2010]Group 部落划分 Group
//在线测评地址https://www.lydsy.com/JudgeOnline/problem.php?id=1821
//最小生成树，去掉合并的边，第一个纳入部落间的最小边，即为答案
//因计算int没有溢出，故不采用long long
//Kruskal算法
//样例通过，提交Compile_Error，一看#include 漏了
//样例通过，提交AC。2019-6-10
#include
#include
#include
#include
#define maxn 1010
using namespace std;
int n,k,cnt=0,f[maxn];
struct Point{
    int x,y;
}p[maxn];
struct node{
    int a,b,v;
}e[maxn*maxn/2];
int dis(Point a,Point b){
    return (a.x-b.x)*(a.x-b.x)+(a.y-b.y)*(a.y-b.y);
}
int cmp(node a,node b){
    return a.v }
int getf(int u){
    return f[u]==u?u:f[u]=getf(f[u]);
}
int merge(int u,int v){
    int f1=getf(u),f2=getf(v);
    if(f1!=f2){
        f[f2]=f1;
        return 1;
    }
    return 0;
}
int main(){
    int i,j,count=0;
    scanf("%d%d",&n,&k);
    for(i=1;i<=n;i++)scanf("%d%d",&p[i].x,&p[i].y);
    for(i=1;i<=n;i++)f[i]=i;
    memset(e,0,sizeof(e));
    for(i=1;i<=n;i++)
        for(j=i+1;j<=n;j++)
            cnt++,e[cnt].a=i,e[cnt].b=j,e[cnt].v=dis(p[i],p[j]);
    sort(e+1,e+1+cnt,cmp);
    for(i=1;i<=cnt;i++)
        if(merge(e[i].a,e[i].b)){
            count++;
            if(count==((n-1)-(k-1)+1)){
                printf("%.2lf\n",sqrt(1.0*e[i].v));
                break;
            }
        }
    return 0;
}

25.bzoj 2134   //2134: 单选错位   //在线测评地址https://www.lydsy.com/JudgeOnline/problem.php?id=2134

//2134: 单选错位
//在线测评地址https://www.lydsy.com/JudgeOnline/problem.php?id=2134
//第一目标，弄懂样例，弄明白，根据以下程序，弄明白了样例输入数据的作用

#include
int a[10000010];
int main(){
    int n,A,B,C;
    scanf("%d%d%d%d%d",&n,&A,&B,&C,a+1);
    for (int i=2;i<=n;i++) a[i] = ((long long)a[i-1] * A + B) % 100000001;
    for (int i=1;i<=n;i++) a[i] = a[i] % C + 1;
    for(int i=1;i<=n;i++)printf("a[%d]=%d\n",i,a[i]);
    return 0;
}
//样例中a序列数据如下

a[1]=2
a[2]=3
a[3]=1
//样例弄懂了，题目怎么做，要学新的内容吗。2019-6-10 20:27

//此文思路相当棒https://www.cnblogs.com/five20/p/9383549.html摘抄如下

BZOJ刷题记录---普及组难度 AC_第16张图片

//此文思路写得不错https://www.luogu.org/problemnew/solution/P1297?page=2摘抄如下

BZOJ刷题记录---普及组难度 AC_第17张图片

//样例通过，提交AC。2019-6-10 22:43
#include
int max(int a,int b){
    return a>b?a:b;
}
int main(){
    int n,A,B,C,a,b,i,x;
    double ans=0;
    scanf("%d%d%d%d%d",&n,&A,&B,&C,&a);
    x=a;
    for(i=2;i<=n;i++)b=((long long)a*A+B)%100000001,ans+=1.0/max(a%C+1,b%C+1),a=b;//此处写成b=b%C+1,ans+=1.0/max(a,b),a=b;
    ans+=1.0/max(x%C+1,b%C+1);//此处写成ans+=1.0/max(x%C+1,b);
    printf("%.3lf\n",ans);
    return 0;
}

2019-8-4 18:00 AC该篇内容．

你可能感兴趣的:(跟着大佬学算法)

  • 分享100个最新免费的高匿HTTP代理IP mcj8089 代理IP代理服务器匿名代理免费代理IP最新代理IP
      推荐两个代理IP网站：   1. 全网代理IP：http://proxy.goubanjia.com/   2. 敲代码免费IP：http://ip.qiaodm.com/     120.198.243.130:80,中国/广东省 58.251.78.71:8088,中国/广东省 183.207.228.22:83,中国/
  • mysql高级特性之数据分区 annan211 java数据结构mongodb分区mysql
    mysql高级特性 1 以存储引擎的角度分析，分区表和物理表没有区别。是按照一定的规则将数据分别存储的逻辑设计。器底层是由多个物理字表组成。 2 分区的原理 分区表由多个相关的底层表实现，这些底层表也是由句柄对象表示，所以我们可以直接访问各个分区。存储引擎管理分区的各个底层 表和管理普通表一样(所有底层表都必须使用相同的存储引擎)，分区表的索引只是
  • JS采用正则表达式简单获取URL地址栏参数 chiangfai js地址栏参数获取
    GetUrlParam:function GetUrlParam(param){ var reg = new RegExp("(^|&)"+ param +"=([^&]*)(&|$)"); var r = window.location.search.substr(1).match(reg); if(r!=null
  • 怎样将数据表拷贝到powerdesigner (本地数据库表) Array_06 powerDesigner
    ================================================== 1、打开PowerDesigner12，在菜单中按照如下方式进行操作 file->Reverse Engineer->DataBase 点击后，弹出 New Physical Data Model 的对话框 2、在General选项卡中 Model name:模板名字，自
  • logbackのhelloworld 飞翔的马甲 日志logback
    一、概述 1.日志是啥？ 当我是个逗比的时候我是这么理解的：log.debug()代替了system.out.print(); 当我项目工作时，以为是一堆得.log文件。 这两天项目发布新版本，比较轻松，决定好好地研究下日志以及logback。 传送门1：日志的作用与方法： http://www.infoq.com/cn/articles/why-and-how-log 上面的作
  • 新浪微博爬虫模拟登陆 随意而生 新浪微博
    转载自：http://hi.baidu.com/erliang20088/item/251db4b040b8ce58ba0e1235     近来由于毕设需要，重新修改了新浪微博爬虫废了不少劲，希望下边的总结能够帮助后来的同学们。      现行版的模拟登陆与以前相比，最大的改动在于cookie获取时候的模拟url的请求
  • synchronized 香水浓 javathread
        Java语言的关键字，可用来给对象和方法或者代码块加锁，当它锁定一个方法或者一个代码块的时候，同一时刻最多只有一个线程执行这段代码。当两个并发线程访问同一个对象object中的这个加锁同步代码块时，一个时间内只能有一个线程得到执行。另一个线程必须等待当前线程执行完这个代码块以后才能执行该代码块。然而，当一个线程访问object的一个加锁代码块时，另一个线程仍然
  • maven 简单实用教程 AdyZhang maven
    1. Maven介绍  1.1. 简介 java编写的用于构建系统的自动化工具。目前版本是2.0.9，注意maven2和maven1有很大区别，阅读第三方文档时需要区分版本。 1.2. Maven资源 见官方网站；The 5 minute test，官方简易入门文档；Getting Started Tutorial，官方入门文档；Build Coo
  • Android 通过 intent传值获得null aijuans android
    我在通过intent 获得传递兑现过的时候报错，空指针,我是getMap方法进行传值，代码如下 1 2 3 4 5 6 7 8 9 public void getMap(View view){            Intent i =
  • apache 做代理 报如下错误：The proxy server received an invalid response from an upstream baalwolf response
    网站配置是apache＋tomcat,tomcat没有报错，apache报错是： The proxy server received an invalid response from an upstream server. The proxy server could not handle the request GET /. Reason: Error reading fr
  • Tomcat6 内存和线程配置 BigBird2012 tomcat6
    1、修改启动时内存参数、并指定JVM时区 （在windows server 2008 下时间少了8个小时） 在Tomcat上运行j2ee项目代码时，经常会出现内存溢出的情况，解决办法是在系统参数中增加系统参数：  window下， 在catalina.bat最前面 set JAVA_OPTS=-XX:PermSize=64M -XX:MaxPermSize=128m -Xms5
  • Karam与TDD bijian1013 KaramTDD
    一.TDD         测试驱动开发（Test-Driven Development,TDD）是一种敏捷（AGILE）开发方法论，它把开发流程倒转了过来，在进行代码实现之前，首先保证编写测试用例，从而用测试来驱动开发（而不是把测试作为一项验证工具来使用）。         TDD的原则很简单： a.只有当某个
  • [Zookeeper学习笔记之七]Zookeeper源代码分析之Zookeeper.States bit1129 zookeeper
    public enum States { CONNECTING, //Zookeeper服务器不可用，客户端处于尝试链接状态 ASSOCIATING, //？？？ CONNECTED, //链接建立，可以与Zookeeper服务器正常通信 CONNECTEDREADONLY, //处于只读状态的链接状态，只读模式可以在
  • 【Scala十四】Scala核心八：闭包 bit1129 scala
    Free variable A free variable of an expression is a variable that’s used inside the expression but not defined inside the expression. For instance, in the function literal expression (x: Int) => (x
  • android发送json并解析返回json ronin47 android
    package com.http.test; import org.apache.http.HttpResponse; import org.apache.http.HttpStatus; import org.apache.http.client.HttpClient; import org.apache.http.client.methods.HttpGet; import
  • 一份IT实习生的总结 brotherlamp PHPphp资料php教程php培训php视频
    今天突然发现在不知不觉中自己已经实习了 3 个月了，现在可能不算是真正意义上的实习吧，因为现在自己才大三，在这边撸代码的同时还要考虑到学校的功课跟期末考试。让我震惊的是，我完全想不到在这 3 个月里我到底学到了什么，这是一件多么悲催的事情啊。同时我对我应该 get 到什么新技能也很迷茫。所以今晚还是总结下把，让自己在接下来的实习生活有更加明确的方向。最后感谢工作室给我们几个人这个机会让我们提前出来
  • 据说是2012年10月人人网校招的一道笔试题-给出一个重物重量为X,另外提供的小砝码重量分别为1，3，9。。。3^N。 将重物放到天平左侧，问在两边如何添加砝码 bylijinnan java
    public class ScalesBalance { /** * 题目： * 给出一个重物重量为X,另外提供的小砝码重量分别为1，3，9。。。3^N。 （假设N无限大，但一种重量的砝码只有一个） * 将重物放到天平左侧，问在两边如何添加砝码使两边平衡 * * 分析： * 三进制 * 我们约定括号表示里面的数是三进制，例如 47=(1202
  • dom4j最常用最简单的方法 chiangfai dom4j
    要使用dom4j读写XML文档,需要先下载dom4j包,dom4j官方网站在 http://www.dom4j.org/目前最新dom4j包下载地址:http://nchc.dl.sourceforge.net/sourceforge/dom4j/dom4j-1.6.1.zip 解开后有两个包,仅操作XML文档的话把dom4j-1.6.1.jar加入工程就可以了,如果需要使用XPath的话还需要
  • 简单HBase笔记 chenchao051 hbase
     一、Client-side write buffer 客户端缓存请求 描述：可以缓存客户端的请求，以此来减少RPC的次数，但是缓存只是被存在一个ArrayList中，所以多线程访问时不安全的。 可以使用getWriteBuffer()方法来取得客户端缓存中的数据。 默认关闭。 二、Scan的Caching 描述： next( )方法请求一行就要使用一次RPC,即使
  • mysqldump导出时出现when doing LOCK TABLES daizj mysqlmysqdump导数据
    　　执行　mysqldump -uxxx -pxxx -hxxx -Pxxxx database tablename > tablename.sql　 导出表时，会报 mysqldump: Got error: 1044: Access denied for user 'xxx'@'xxx' to database 'xxx' when doing LOCK TABLES 解决
  • CSS渲染原理 dcj3sjt126com Web
      从事Web前端开发的人都与CSS打交道很多，有的人也许不知道css是怎么去工作的，写出来的css浏览器是怎么样去解析的呢？当这个成为我们提高css水平的一个瓶颈时，是否应该多了解一下呢？          一、浏览器的发展与CSS           
  • 《阿甘正传》台词 dcj3sjt126com
    Part Ⅰ: 《阿甘正传》Forrest Gump经典中英文对白 Forrest: Hello! My names Forrest. Forrest Gump. You wanna Chocolate? I could eat about a million and a half othese. My momma always said life was like a box ochocol
  • Java处理JSON dyy_gusi json
    Json在数据传输中很好用，原因是JSON 比 XML 更小、更快，更易解析。 在Java程序中，如何使用处理JSON，现在有很多工具可以处理，比较流行常用的是google的gson和alibaba的fastjson，具体使用如下： 1、读取json然后处理 class ReadJSON { public static void main(String[] args)
  • win7下nginx和php的配置 geeksun nginx
    1.  安装包准备 nginx :  从nginx.org下载nginx-1.8.0.zip php： 从php.net下载php-5.6.10-Win32-VC11-x64.zip， php是免安装文件。 RunHiddenConsole: 用于隐藏命令行窗口   2. 配置 # java用8080端口做应用服务器，nginx反向代理到这个端口即可 p
  • 基于2.8版本redis配置文件中文解释 hongtoushizi redis
    转载自： http://wangwei007.blog.51cto.com/68019/1548167        在Redis中直接启动redis-server服务时, 采用的是默认的配置文件。采用redis-server   xxx.conf 这样的方式可以按照指定的配置文件来运行Redis服务。下面是Redis2.8.9的配置文
  • 第五章 常用Lua开发库3-模板渲染 jinnianshilongnian nginxlua
    动态web网页开发是Web开发中一个常见的场景，比如像京东商品详情页，其页面逻辑是非常复杂的，需要使用模板技术来实现。而Lua中也有许多模板引擎，如目前我在使用的lua-resty-template，可以渲染很复杂的页面，借助LuaJIT其性能也是可以接受的。   如果学习过JavaEE中的servlet和JSP的话，应该知道JSP模板最终会被翻译成Servlet来执行；而lua-r
  • JZSearch大数据搜索引擎 颠覆者 JavaScript
    系统简介： 大数据的特点有四个层面：第一，数据体量巨大。从TB级别，跃升到PB级别；第二，数据类型繁多。网络日志、视频、图片、地理位置信息等等。第三，价值密度低。以视频为例，连续不间断监控过程中，可能有用的数据仅仅有一两秒。第四，处理速度快。最后这一点也是和传统的数据挖掘技术有着本质的不同。业界将其归纳为4个“V”——Volume，Variety，Value，Velocity。大数据搜索引
  • 10招让你成为杰出的Java程序员 pda158 java编程框架
    如果你是一个热衷于技术的  Java 程序员， 那么下面的 10 个要点可以让你在众多 Java 开发人员中脱颖而出。 　　 1. 拥有扎实的基础和深刻理解 OO 原则 　　对于 Java 程序员，深刻理解 Object Oriented Programming（面向对象编程）这一概念是必须的。没有 OOPS 的坚实基础，就领会不了像 Java 这些面向对象编程语言
  • tomcat之oracle连接池配置 小网客 oracle
    tomcat版本7.0 配置oracle连接池方式： 修改tomcat的server.xml配置文件： <GlobalNamingResources> <Resource name="utermdatasource" auth="Container" type="javax.sql.DataSou
  • Oracle 分页算法汇总 vipbooks oraclesql算法.net
        这是我找到的一些关于Oracle分页的算法，大家那里还有没有其他好的算法没？我们大家一起分享一下！ -- Oracle 分页算法一 select * from ( select page.*,rownum rn from (select * from help) page -- 20 = (currentPag
按字母分类： ABCDEFGHIJKLMNOPQRSTUVWXYZ其他