GNN Pooling(八):STRUCTPOOL via CRF,ICLR2020
目录
- 图模型
- 三个马尔科夫性
- 联合概率分布
- CRF
- 以词性标注为例
- STRUCTPOOL
- 实验
- References
本文的作者来自Texas A&M University。大多数现有的图池技术没有显式地考虑图的结构信息,本文将图池看作是一个节点聚类问题,需要学习一个聚类分配矩阵。我们建议将其表示为一个结构化预测问题,并使用条件随机场来捕获不同节点分配之间的关系。使用CRF的直觉是这样的: 给定节点的分配应该依赖于输入节点特性和其他节点的分配,而CRF正是通过无向图模型捕获不同节点分配之间的这种高阶结构关系。
图模型

所谓概率图模型,就是由图表示的概率分布。无向图模型之所以被称为马尔科夫随机场,是因为其联合概率分布需要满足成对马尔科夫性,或者局部马尔科夫性,或者全局马尔科夫性。这三个马尔科夫性是等价的。
三个马尔科夫性
成对马尔科夫性
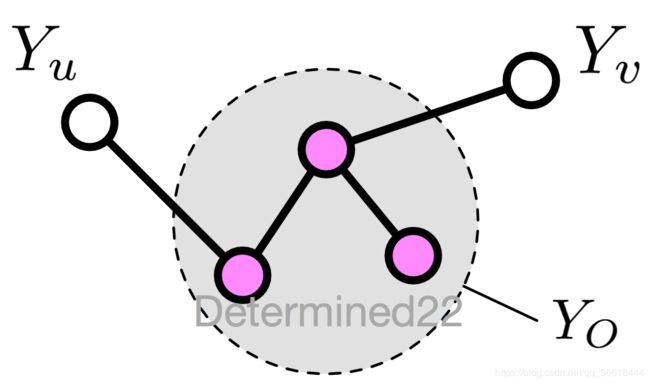
假设 Y u Y_u Yu和 Y v Y_v Yv是不相邻的两个节点, Y o Y_o Yo是所有其他的节点,那么成对马尔科夫性则是说:给定 Y o Y_o Yo则 Y u Y_u Yu和 Y v Y_v Yv相互独立: P ( Y u , Y v ∣ Y O ) = P ( Y u ∣ Y O ) P ( Y v ∣ Y O ) P(Y_u,Y_v|Y_O)=P(Y_u|Y_O)P(Y_v|Y_O) P(Yu,Yv∣YO)=P(Yu∣YO)P(Yv∣YO)
局部马尔科夫性
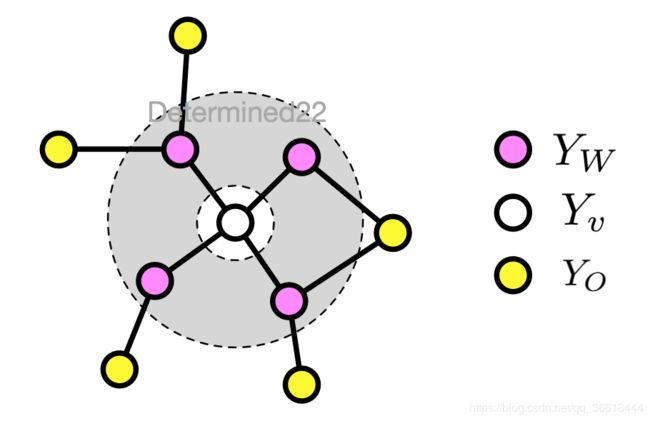
Y v Y_v Yv是任一节点,给定 Y v Y_v Yv的所有邻居 Y w Y_w Yw,则 Y o Y_o Yo和 Y v Y_v Yv相互独立: P ( Y u , Y O ∣ Y W ) = P ( Y u ∣ Y W ) P ( Y O ∣ Y W ) P(Y_u,Y_O|Y_W)=P(Y_u|Y_W)P(Y_O|Y_W) P(Yu,YO∣YW)=P(Yu∣YW)P(YO∣YW)
全局马尔科夫性

设节点集合 A 、B 是在无向图 G 中被节点集合 C 分开的任意节点集合,全局马尔可夫性指:给定 Y C Y_C YC的条件下, Y A Y_A YA 和 Y B Y_B YB 条件独立。
联合概率分布
整个概率无向图模型的联合概率分布 P ( Y ) P(Y) P(Y)可以用最大团上的随机变量的函数的乘积来表示,称为概率无向图的因子分解:
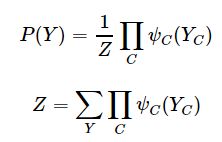
其中,、 ψ C ( Y C ) ψ_C(Y_C) ψC(YC)表示最大团 C C C的势函数(potential function), Y Y Y指整个图的所有点集。 ψ C ( Y C ) ψ_C(Y_C) ψC(YC)这个函数是需要人为给出的,势函数严格要求为正数,所以一般用指数函数来写:
![]()
CRF
条件随机场是给定一组变量X的条件下输出另一组随机变量Y的马尔科夫随机场。我也按照大多数介绍的那样,用线性条件随机场举例。
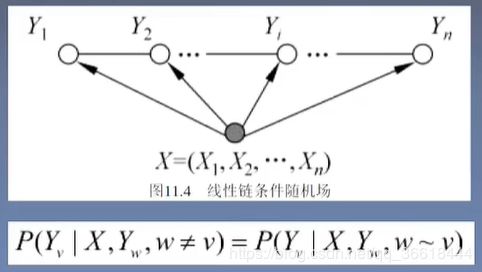
w − v w-v w−v表示和v相邻的所有结点,也就是说,在给定X的大前提下, Y v Y_v Yv只由其相邻的结点w决定。对于链来说,这个相邻节点就是v的左右两个节点,而最大团则是相邻的两个节点。因此,线性CRF写成如下的表达形式:
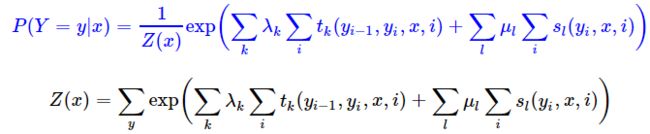
其中 Z ( x ) Z(x) Z(x)表示归一化系数,是对 y y y所有可能取值的求和。 y i − 1 y_{i-1} yi−1和 y i y_i yi则表示一个最大团,则 t k t_k tk定义了转移特征, s l s_l sl定义了状态特征, i i i表示当前节点, x x x为给定的条件,需要学习的参数为 λ k λ_k λk和 μ l μ_l μl。一般来说,特征函数的取值为 1 或 0 ,当满足规定好的特征条件时取值为 1 ,否则为 0 。
以词性标注为例
词性标注是CRF最常解决的问题,我们在具体的任务中理解上述线性CRF的公式含义。首先看状态特征 s l s_l sl,其由三个输入参数决定: y i y_i yi表示当前的单词的词性(名词动词啦等等), x x x为给定的条件,这个一般是处理好的单词的embedding,比如在LSTM+CRF进行词性标注时, x x x就表示LSTM的hidden state, i i i表示当前的位置,状态特征只由单词本身的特征决定。 t k t_k tk是转移特征,因此需要 y i − 1 y_{i-1} yi−1与 y i y_i yi两个参数,表明前一个单词是一个特定词性下对后一个单词的影响。尽管 t k t_k tk与 s l s_l sl只取值0,1,但是通过学习参数 λ k λ_k λk和 μ l μ_l μl就可以做到调节其概率。
STRUCTPOOL
终于说到本文的模型了。
对于原始图G中的任意节点,其聚类分配不仅要依赖于节点特征矩阵X,还要依赖于其他节点的聚类分配。形式上定义了 Y = [ Y 1 , . . . Y n ] Y=[Y_1,...Y_n] Y=[Y1,...Yn],其中 Y i ∈ [ 1... k ] Y_i∈[1...k] Yi∈[1...k],表明每个结点被分配到哪个cluster。而 X X X被视为全局观测特征,然后就可以通过吉布斯分布去定义CRF:
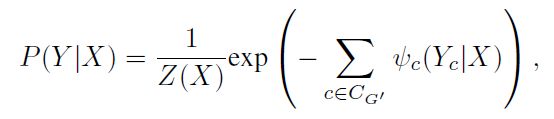
其中, C C C就是clique, C G ′ C_{G^{'}} CG′是图中所有clique的集合, Z ( X ) Z(X) Z(X)是归一化的系数, ψ c ( ⋅ ) ψ_c(·) ψc(⋅)是势函数。吉布斯能量可以写成:

这个可以理解为是上一个公式括号里负号之后的内容,所以整个目标是求解 P ( Y ∣ X ) P(Y|X) P(Y∣X)最大的过程,也就是求 E ( y ∣ X ) E(y|X) E(y∣X)最小的过程。对于每个团c内部的能量,本文考虑到了两个部分:一是每个节点被分配给一个团的能量(unary energy),还有同一个团内任意两个节点之间可达性的能量(pairwise energy),这个可达性本质上就是对图拓扑结构的一种具象化表示。总体的能量写成:
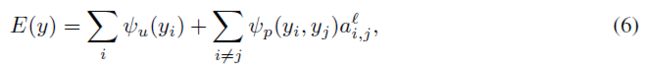
其中, ψ u ( y i ) ψ_u(y_i) ψu(yi)表示结点i被分配给cluster y的能量, ψ p ( y i , y j ) ψ_p(y_i,y_j) ψp(yi,yj)节点对被一同分配给同一个cluster的能量,这个势函数用注意力机制进行计算。 a i , j l a^l_{i,j} ai,jl则表示节点i,j在图中 l − h o p l-hop l−hop可达。使用注意力机制计算的pairwise energy表示为:

μ ( y i , y j ) μ(y_i,y_j) μ(yi,yj) a compatibility function that models the compatibility between different assignment pairs(这句话我就不翻译了)。总体的算法流程如下:

更直观的可视化为:
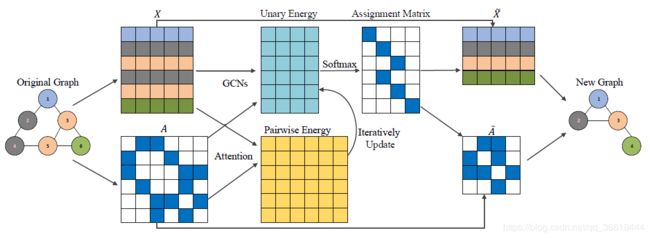
实验

在统一架构下比较不同的池化方法:
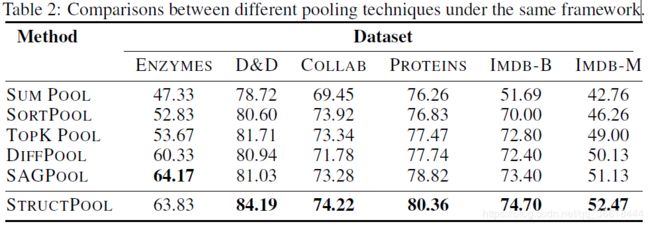
除了上述两组基础的试验外,还对一些模型细节进行了探究:
- COMPUTATIONAL COMPLEXITY。计算复杂度是这种需要划分clique的池化需要考虑的重要问题,因为这种方法的时间复杂度往往都比较高。本文也给出了计算复杂度,近似为 O ( ( m + i ) n 3 ) O((m+i)n^3) O((m+i)n3),其中 m m m是迭代次数 i i i是为了获取unary energy所需的GCN的层数。下表探究了m的次数对分类结果的影响:
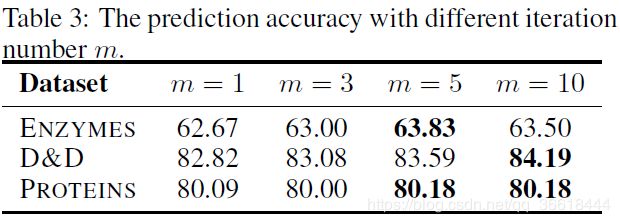
分类的性能当然随着m的增加而增加,一般到5是一个很好的平衡点。STRUCTPOOL对于m = 1、m = 3、m = 5分别需要0.049秒、0.053秒和0.058秒,而对应的DiffPool每个图的平均池化时间则为0.042。- EFFECTS OF TOPOLOGY INFORMATION。上文也提到了 l l l是引入拓扑结构的关键。 l l l越大也就代表clique内部的关系越稠密,模型考虑了更多的成对关系,因此获得更好的性能是合理的。但是对于IMDB-B这种在one-hop下就可以学习到很多有用信息的数据集,多跳反而对结果的影响不大。
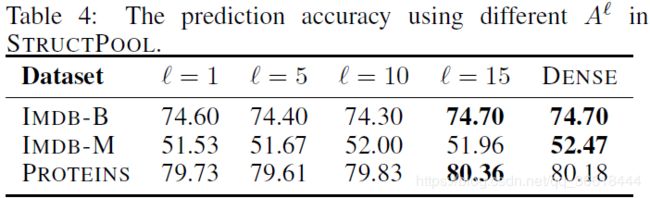
- GRAPH ISOMORPHISM NETWORKS WITH STRUCTPOOL。和另外一个模型Graph Isomorphism Networks(GIN)进行比较,证实了算法结果的更优。

References
https://www.cnblogs.com/Determined22/p/6915730.html
https://www.bilibili.com/video/BV11E411n7rE?from=search&seid=29122248621740294
https://blog.csdn.net/qq_35883464/article/details/99852915