焦点损失函数 Focal Loss 与 GHM

文章来自公众号【机器学习炼丹术】

1 focal loss的概述

焦点损失函数 Focal Loss（2017年何凯明大佬的论文）被提出用于密集物体检测任务。

当然，在目标检测中，可能待检测物体有1000个类别，然而你想要识别出来的物体，只是其中的某一个类别，这样其实就是一个样本非常不均衡的一个分类问题。

而Focal Loss简单的说，就是解决样本数量极度不平衡的问题的。

说到样本不平衡的解决方案，相比大家是知道一个混淆矩阵的f1-score的，但是这个好像不能用在训练中当成损失。而Focal loss可以在训练中，让小数量的目标类别增加权重，让分类错误的样本增加权重。

先来看一下简单的二值交叉熵的损失：

• y’是模型给出的预测类别概率，y是真实样本。就是说，如果一个样本的真实类别是1，预测概率是0.9，那么\(-log(0.9)\)就是这个损失。
• 讲道理，一般我不喜欢用二值交叉熵做例子，用多分类交叉熵做例子会更舒服。

---

【然后看focal loss的改进】：

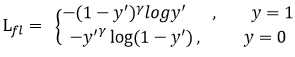
这个增加了一个\((1-y')^\gamma\)的权重值，怎么理解呢？就是如果给出的正确类别的概率越大，那么\((1-y')^\gamma\)就会越小，说明分类正确的样本的损失权重小，反之，分类错误的样本的损权重大。

---

【focal loss的进一步改进】：

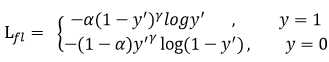
这里增加了一个\(\alpha\)，这个alpha在论文中给出的是0.25,这个就是单纯的降低正样本或者负样本的权重，来解决样本不均衡的问题。

两者结合起来，就是一个可以解决样本不平衡问题的损失focal loss。

---

【总结】：

1. \(\alpha\)解决了样本的不平衡问题；
2. \(\beta\)解决了难易样本不平衡的问题。让样本更重视难样本，忽视易样本。
3. 总之，Focal loss会的关注顺序为：样本少的、难分类的；样本多的、难分类的；样本少的，易分类的；样本多的，易分类的。

2 GHM

• GHM是Gradient Harmonizing Mechanism。

这个GHM是为了解决Focal loss存在的一些问题。

【Focal Loss的弊端1】
让模型过多的关注特别难分类的样本是会有问题的。样本中有一些异常点、离群点（outliers）。所以模型为了拟合这些非常难拟合的离群点，就会存在过拟合的风险。

2.1 GHM的办法

Focal Loss是从置信度p的角度入手衰减loss的。而GHM是一定范围内置信度p的样本数量来衰减loss的。

首先定义了一个变量g，叫做梯度模长（gradient norm）：

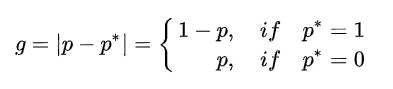
可以看出这个梯度模长，其实就是模型给出的置信度\(p^*\)与这个样本真实的标签之间的差值（距离）。g越小，说明预测越准，说明样本越容易分类。

下图中展示了g与样本数量的关系：

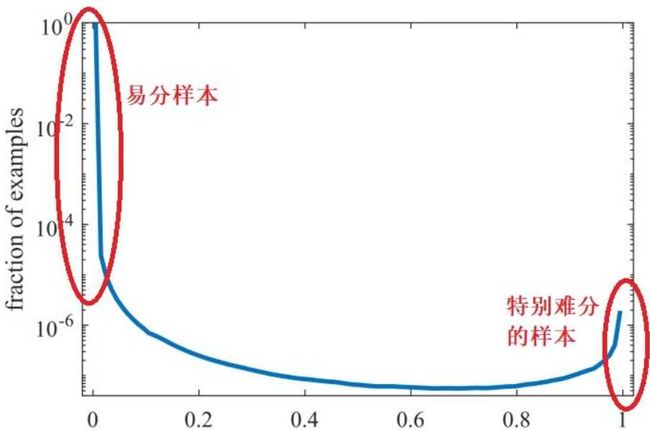
【从图中可以看到】

• 梯度模长接近于0的样本多，也就是易分类样本是非常多的
• 然后样本数量随着梯度模长的增加迅速减少
• 然后当梯度模长接近1的时候，样本的数量又开始增加。

GHM是这样想的，对于梯度模长小的易分类样本，我们忽视他们；但是focal loss过于关注难分类样本了。关键是难分类样本其实也有很多！,如果模型一直学习难分类样本，那么可能模型的精确度就会下降。所以GHM对于难分类样本也有一个衰减。

那么，GHM对易分类样本和难分类样本都衰减，那么真正被关注的样本，就是那些不难不易的样本。而抑制的程度，可以根据样本的数量来决定。

这里定义一个GD，梯度密度：

\[GD(g)=\frac{1}{l(g)}\sum_{k=1}^N{\delta(g_k,g)} \]

• \(GD(g)\)是计算在梯度g位置的梯度密度；
• \(\delta(g_k,g)\)就是样本k的梯度\(g_k\)是否在\([g-\frac{\epsilon}{2},g+\frac{\epsilon}{2}]\)这个区间内。
• \(l(g)\)就是\([g-\frac{\epsilon}{2},g+\frac{\epsilon}{2}]\)这个区间的长度，也就是\(\epsilon\)

总之，\(GD(g)\)就是梯度模长在\([g-\frac{\epsilon}{2},g+\frac{\epsilon}{2}]\)内的样本总数除以\(\epsilon\).

然后把每一个样本的交叉熵损失除以他们对应的梯度密度就行了。

\[L_{GHM}=\sum^N_{i=1}{\frac{CE(p_i,p_i^*)}{GD(g_i)}} \]

• \(CE(p_i,p_i^*)\)表示第i个样本的交叉熵损失；
• \(GD(g_i)\)表示第i个样本的梯度密度；

2.2 论文中的GHM

论文中呢，是把梯度模长划分成了10个区域，因为置信度p是从0~1的，所以梯度密度的区域长度就是0.1，比如是0~0.1为一个区域。

下图是论文中给出的对比图：

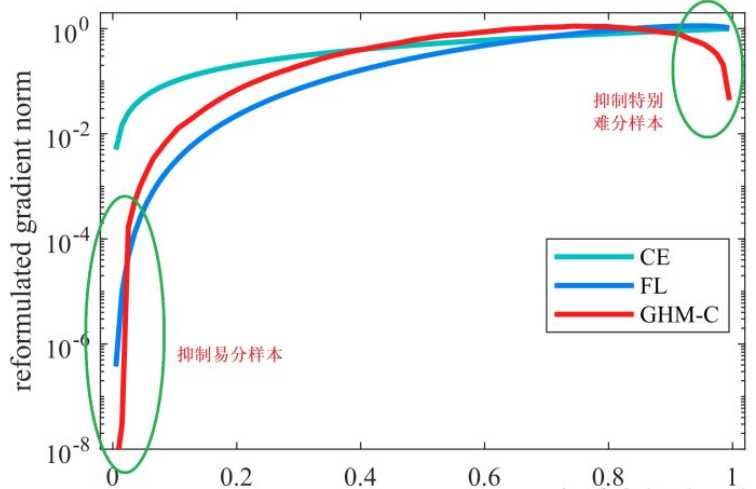
【从图中可以得到】

• 绿色的表示交叉熵损失；
• 蓝色的是focal loss的损失，发现梯度模长小的损失衰减很有效；
• 红色是GHM的交叉熵损失，发现梯度模长在0附近和1附近存在明显的衰减。

当然可以想到的是，GHM看起来是需要整个样本的模型估计值，才能计算出梯度密度，才能进行更新。也就是说mini-batch看起来似乎不能用GHM。

在GHM原文中也提到了这个问题，如果光使用mini-batch的话，那么很可能出现不均衡的情况。

【我个人觉得的处理方法】

1. 可以使用上一个epoch的梯度密度，来作为这一个epoch来使用；
2. 或者一开始先使用mini-batch计算梯度密度，然后模型收敛速度下降之后，再使用第一种方式进行更新。

3 python实现

上面讲述的关键在于focal loss实现的功能：

1. 分类正确的样本的损失权重小，分类错误的样本的损权重大。
2. 样本过多的类别的权重较小

在CenterNet中预测中心点位置的时候，也是使用了Focal Loss，但是稍有改动。

3.1 概述

这里面和上面讲的比较类似，我们忽视脚标。

• 假设\(Y=1\),那么预测的\(\hat{Y}\)越靠近1，说明预测的约正确，然后\((1-\hat{Y})^\alpha\)就会越小，从而体现分类正确的样本的损失权重小;otherwize的情况也是这样。
• 但是这里的otherwize中多了一个\((1-Y)^\beta\),这个是用来平衡样本不均衡问题的，在后面的代码部分会提到CenterNet的热力图。就会明白这个了。

3.2 代码讲解

下面通过代码来理解：

class FocalLoss(nn.Module):
    def __init__(self):
        super().__init__()
        self.neg_loss = _neg_loss

    def forward(self, output, target, mask):
        output = torch.sigmoid(output)
        loss = self.neg_loss(output, target, mask)
        return loss

这里面的output可以理解为是一个1通道的特征图，每一个pixel的值都是模型给出的置信度，然后通过sigmoid函数转换成0~1区间的置信度。

而target是CenterNet的热力图，这一点可能比较难理解。打个比方，一个10*10的全都是0的特征图，然后这个特征图中只有一个pixel是1，那么这个pixel的位置就是一个目标检测物体的中心点。有几个1就说明这个图中有几个要检测的目标物体。

然后，如果一个特征图上，全都是0，只有几个孤零零的1，未免显得过于稀疏了，直观上也非常的不平滑。所以CenterNet的热力图还需要对这些1为中心做一个高斯

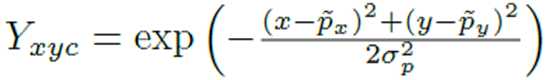
可以看作是一种平滑：

可以看到，数字1的四周是同样的数字。这是一个以1为中心的高斯平滑。

---

这里我们回到上面说到的\((1-Y)^\beta\)：

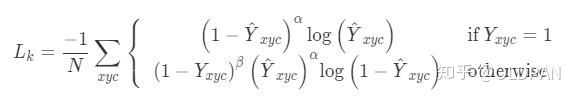
对于数字1来说，我们计算loss自然是用第一行来计算，但是对于1附近的其他点来说，就要考虑\((1-Y)^\beta\)了。越靠近1的点的\(Y\)越大，那么\((1-Y)^\beta\)就会越小，这样从而降低1附近的权重值。其实这里我也讲不太明白，就是根据距离1的距离降低负样本的权重值，从而可以实现样本过多的类别的权重较小。

---

我们回到主题，对output进行sigmoid之后，与output一起放到了neg_loss中。我们来看什么是neg_loss:

def _neg_loss(pred, gt, mask):
    pos_inds = gt.eq(1).float() * mask
    neg_inds = gt.lt(1).float() * mask

    neg_weights = torch.pow(1 - gt, 4)

    loss = 0

    pos_loss = torch.log(pred) * torch.pow(1 - pred, 2) * pos_inds
    neg_loss = torch.log(1 - pred) * torch.pow(pred, 2) * \
               neg_weights * neg_inds

    num_pos = pos_inds.float().sum()
    pos_loss = pos_loss.sum()
    neg_loss = neg_loss.sum()

    if num_pos == 0:
        loss = loss - neg_loss
    else:
        loss = loss - (pos_loss + neg_loss) / num_pos
    return loss

先说一下，这里面的mask是根据特定任务中加上的一个小功能，就是在该任务中，一张图片中有一部分是不需要计算loss的，所以先用过mask把那个部分过滤掉。这里直接忽视mask就好了。

从neg_weights = torch.pow(1 - gt, 4)可以得知\(\beta=4\),从下面的代码中也不难推出，\(\alpha=2\)，剩下的内容就都一样了。

把每一个pixel的损失都加起来，除以目标物体的数量即可。