数据结构与算法（二）：数组

注：我们先由简到难总结一下常用的数据结构，如简单数组、链表、散列表、队列、栈、树、图等等，最后再来研讨算法。

一、线性表

线性表是很基本的一种数据结构，就如字面意思一样，它把若干数据线性组合在一起：每个元素都最多只有前相邻和后相邻元素，也就是元素之间首尾相接。典型的线性表结构有数组、链表、栈、队列等。它有一些特征（摘自百度百科）：

          1．集合中必存在唯一的一个“第一元素”。

          2．集合中必存在唯一的一个 “最后元素” 。

          3．除最后一个元素之外，均有唯一的后继(后件)。

          4．除第一个元素之外，均有唯一的前驱(前件)。

注意：循环链表也是一种线性表结构，只是第一个元素和最后一个元素首尾相连。

二、数组

数组是一种元素序列，本身就是一种线性表结构，它用一块连续的内存空间把相同类型的一些元素无序的组合起来（关于相同类型的说法并不是绝对的，比如VFP中并没有要求数组中必须存储相同类型的元素，我们只是站在数据结构的角度这样说）。关于数组，相信大家都很熟悉，用的也比较多，特性之类的也比较了解，我们只需要强调一点，就是数组怎么实现“随机访问”时间复杂度为O(1)的？

这里面有关键的两点，一是它的内存空间是连续的，二是存储相同的数据类型。具体是什么意思呢？我们在malloc(动态分配)一块内存的时候，会指定所需空间的大小，比如：

int *p = (int*) malloc(sizeof(int) * 10);

我们要创建一个数组，那么一开始就确定了类型：type，同时我们指定数量：n，那么需要的内存空间大小就能直接算出来：sizeof(type) * n。malloc函数分配该大小的内存空间，如果成功会返回指向被分配内存空间的指针，该指针指向此内存区域的起始地址。当然我们需要把void *类型转换为我们确定的类型，比如int *。

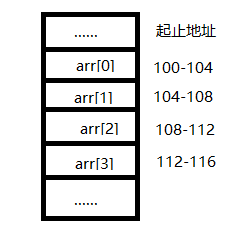
对于32位CPU，内存地址由32位无符号整数表示，我们这里为了方便讲解，不会涉及到逻辑地址、物理地址等概念，图中的描述也会尽可能的简单，能理解意思就行。比如我们现在创建一个长度为4的int数组arr，并且完成了赋值，其内存布局如下图所示，该内存空间的起始地址为100，arr[0]到arr[3]四个元素的地址紧紧挨着，且每个元素占4个单位的内存空间。

malloc成功之后，int *p就为指向100地址的指针，100-104就存放着我们的arr[0]，所以我们能够不用循环操作直接获取arr[0]，时间复杂度为O(1)。现在我们要完成一个随机访问：返回arr[2]，怎么处理呢？由于地址空间是连续的，且元素类型是已知的，我们就可以直接算出来arr[2]的起始地址：address = 100 + 4*2=108，结合图中，arr[2]所在的内存起始地址确实为108，然后就可以获取108 -108+4这块内存区域存放的数据了。我们发现，这里同样没有用循环操作就直接获取了对应下标的数据，虽然多了一个计算操作，但只需要计算一次，和n的规模无关，所以时间复杂度也为O(1)。

所以我们就得出了数组通过下标访问的寻址方式：

                                     address_n = base_address + n * sizeof (type)，其时间复杂度为O(1)。

到这里我们就能理解，为什么数组的下标是以0开始的呢？如果以1开始的话，那么我们的寻址计算公式就得变一变：

                                     address_n = base_address + (n - 1) * sizeof (type)。

明显多了一次-1的操作o(╯□╰)o。

我们都知道，数组的最大优点是：随机访问时间复杂度为O(1)（注意：数组只是通过下标访问其时间复杂度为O(1),如果要寻找和某指定元素相同的值，其时间复杂度可不为O(1)！如果使用顺序查找则为O(n)，即使是排好序的数组使用二分法查找也为O(logn)。我经常在面试中问应聘者：数组查找元素的时间复杂度？大多数人都会毫不犹豫的说：O(1)）。另外数组的删除元素和插入元素相对来说就不那么高效，平均时间复杂度为O(n)，感兴趣的小伙伴可以根据时间复杂度和空间复杂度提到的内容自己算一算。

注：考虑到数组的特性，我们最好在使用之前就确定好(或者有个大致的上限标准)我们需要存储的元素数量，因为数组不同于我们接下来会聊的链表，它需要占用连续的内存空间。如果我们实际使用的容量和申请的容量相差太大的话，会对内存空间造成比较大的浪费，另外我们也要尽可能避免数组的扩容，也就是咱们申请空间既不能太大，也不能太小。单纯使用数组可能还好些，但是一些高级语言可能使用数组实现了一些“复杂”点儿的结构，它们隐藏了一些细节。比如JAVA里的List，我们单纯的new ArrayList()；其实生成的是一个空数组，同时它有一些自己的扩容指标和方式，我们需要尽可能的避免Arrays.copyOf的发生。

三、扩展：二维数组

前面我们总结了一维数组的基础知识，那么我们思考一下二维数组又是怎样的呢？其查找元素时间复杂度又是怎样的呢？(这也是我经常会问应聘者的问题，哈哈O(∩_∩)O)。

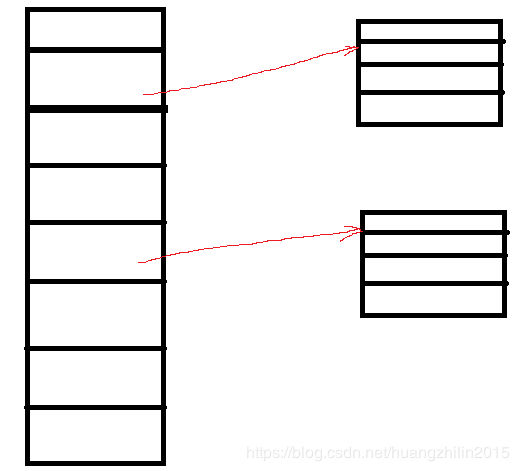
很多人的第一反应可能都是，二维数组嘛，简单！我们就在一维数组的基础上进行扩展：一维数组中的每个元素又是一个一维数组。当然，这种结构看起来是没有问题的，能够达到我们二维的要求。如下图所示：

我们来分析一下此结构的内存分配和寻址，以mXn（m行，n列）的二维数组举例。

首先是内存分配：先分配m个长度的一维内存空间，在这之前我们需要知道元素个数和每个元素需要占的空间大小。元素个数我们知道=m，每个元素占的空间大小呢？这里就不是sizeof(type)了，由于我们每个元素本身又是一个一维数组，所以元素只需要存数组的起始地址指针，所以应该是sizeof(pointer)，比如32位系统中为4个字节。看起来倒还是简单，但是这个指针怎么来呢？还是要通过malloc返回。所以我们还需要另外分配 m 个 n * sizeof(type)的内存空间，并且将这些空间的起始地址绑定到m一维数组的每个元素上。不论我们是一个元素一个元素的分配，还是分配完之后再进行赋值，是不是感觉都很麻烦？

然后是寻址方式：如果我们要寻找3行2列的元素，也就是array[3][2]，怎么处理呢？首先定位到第三行，address_3 = base_address + 3 * sizeof(pointer)，这里address_3的值还是一个指针，指向一个地址（另一个一维数组的起始地址）。接下来定位第二列，addres_3_2 = address_3->data + 2 * sizeof(type)。

从上面的描述可以看出来，其随机访问时间复杂度还是为O(1)。但是不论是内存分配，还是寻址都很麻烦，会做很多操作。那么该怎么存储“简单”点儿呢？答案就是仍然用一维数组存储二维数据。

我们还是以mXn的二维数组来举例子，首先来看内存分配：由于我们还是使用一维的结构存储，那么需要总空间可以这样算：m*n*sizeof(type)，然后返回指向这块内存起始地址的指针。但是二维数组的结构又该怎么在一维中体现呢？

我们把二维数组中的数据按行的顺序依次存入一维数组中，即先存入第一行，再接着存入第二行，其中存每行的时候按照第一列到最后一列的顺序，就这样依次循环把所有行都存入一维数组。比如我们创建2X3的数组，则元素的存入顺序就是：arr[0][0]、arr[0][1]、arr[0][2]、arr[1][0]、arr[1][1]、arr[1[2]，如下图所示（为了方便放图，我这里横向作图哈）：

可以看出来，我们其实是“跳起来”存的，这种思想在很多地方都有体现，后面在聊更多的数据结构和算法的时候会提到。那么针对这种结构我们又该怎样寻址呢？其实很简单。比如上图中的2X3的例子，我们要找arr[i][j]的元素。现在令i=1，j=2，也就是要找arr[1][2]的元素，该怎么定位呢？由于i=1，所以我们要跳过1*n个元素(n==3)，跳过之后还要找到第j个元素，所以再+j就可以了，所以arr[1][2]的地址为：base_address + (1 * 3 + 2) * sizeof(type)。

所以我们得出，在mXn的二维数组中要定位到arr[i][j]的地址，只需要这样做：base_address + (i * n + j) * sizeof(type)。是不是简单多了？（小伙伴们可以试试按列存储的话，又该是怎么一种情况）

四、总结

数组作为一种我们常用的数据结构，在使用之前我们要明确它的优缺点，想清楚适不适合采取这一数据结构。而数据结构的魅力就在于，很多情况我们都可以使用多种不同的数据结构解决我们的问题，但是不同的数据结构适合不同的应用场景(简单说来就是增删改查)，用“错”了数据结构，虽说结果可能没有差别，但是算法的性能可能会有天壤之别；同时就如前面提到的JAVA的ArrayList，我们要用好这些高级语言提供给我们的“工具”，就需要我们清楚其原理，这样才能在合适的地方使用合适的运用方式，这也是我们每个做研发的人员必须掌握这些基础知识的原因。

注：本文是博主的个人理解，如果有错误的地方，希望大家不吝指出，谢谢