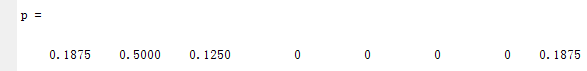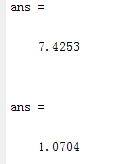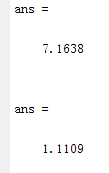十四、数字图像处理之图像压缩
图像压缩
- （一）概念
- （二）编码冗余
- （1）霍夫曼码
- （2）霍夫曼编码
- （3）霍夫曼译码
- （三）空间冗余
- （四）不相关的信息
- （五）JPEG压缩
- （1）JPEG
- （2）JPEG2000
- （六）视频压缩
- （1）Matlab图像序列和电影
- （2）时间冗余和运动补偿
（一）概念
图像压缩就是减少表示数字图像时需要的数据量，是通过去除一个或三个基本数据冗余来得到的。主要有三类，分别是编码冗余、空间或/和时间冗余、不相干冗余。
-
图像数据的冗余主要表现为：图像中相邻像素间的相关性引起的空间冗余；图像序列中不同帧之间存在相关性引起的时间冗余；不同彩色平面或频谱带的相关性引起的频谱冗余。由于图像数据量的庞大，在存储、传输、处理时非常困难,因此图像数据的压缩就显得非常重要。
-
图像压缩可以是有损数据压缩也可以是无损数据压缩。对于如绘制的技术图、图表或者漫画优先使用无损压缩，这是因为有损压缩方法，尤其是在低的位速条件下将会带来压缩失真。如医疗图像或者用于存档的扫描图像等这些有价值的内容的压缩也尽量选择无损压缩方法。有损方法非常适合于自然的图像，例如一些应用中图像的微小损失是可以接受的（有时是无法感知的），这样就可以大幅度地减小位速。（来自百度百科）
-
通用的图像压缩系统如下图所示：主要是通过编码器和解码器组成。
获取图像压缩质量的好坏是通过计算其压缩比得到的，公式为：
在matlab中用函数imratio进行计算图像压缩后的压缩比：
function cr = imratio(f1, f2)
%IMRATIO Computes the ratio of the bytes in two images/variables.
% CR = IMRATIO(F1, F2) returns the ratio of the number of bytes in
% variables/files F1 and F2. If F1 and F2 are an original and
% compressed image, respectively, CR is the compression ratio.
% Copyright 2002-2004 R. C. Gonzalez, R. E. Woods, & S. L. Eddins
% Digital Image Processing Using MATLAB, Prentice-Hall, 2004
% $Revision: 1.4 $ $Date: 2003/11/21 13:11:15 $
error(nargchk(2, 2, nargin)); % Check input arguments
cr = bytes(f1) / bytes(f2); % Compute the ratio
%-------------------------------------------------------------------%
function b = bytes(f)
% Return the number of bytes in input f. If f is a string, assume
% that it is an image filename; if not, it is an image variable.
if ischar(f)
info = dir(f); b = info.bytes;
elseif isstruct(f)
% MATLAB's whos function reports an extra 124 bytes of memory
% per structure field because of the way MATLAB stores
% structures in memory. Don't count this extra memory; instead,
% add up the memory associated with each field.
b = 0;
fields = fieldnames(f);
for k = 1:length(fields)
b = b + bytes(f.(fields{k}));
end
else
info = whos('f'); b = info.bytes;
end
调用这个函数：
r = imratio(imread('C:\Users\Public\Pictures\Sample Pictures\cat.jpg'),'C:\Users\Public\Pictures\Sample Pictures\cat.jpg')
这就得到了图像的压缩比。
（二）编码冗余
说明：编码冗余就是当所用的码字大于最佳编码（也就是最小长度）时存在的冗余。还提到了熵的概念，查了资料得到：熵（entropy）指的是体系的混乱的程度，它在控制论、概率论、数论、天体物理、生命科学等领域都有重要应用，在不同的学科中也有引申出的更为具体的 定义，是各领域十分重要的参量。这里我们讨论的是图像处理中的熵，图像熵是一种特征的统计形式，它反映了图像中平均信息量的多少。
图像熵数学公式为：
计算熵可以调用函数ntrop来处理：
function h = ntrop(x,n)
error(nargchk(1,2,nargin));
if nargin < 2
n = 256;
end
x = double(x);
xh = hist(x(:),n);
xh = xh /sum(xh(:));
i = find(xh);
h = -sum(xh(i)).*log2(xh(i));
编写实验代码：
f = [119 123 168 119;123 119 168 168];
f = [f;119 119 107 119;107 107 119 119]
p =hist(f(:),8);
[p x]=hist(f(:),8),title('向量f的直方图显示')
p = p/sum(p) %直方图各个灰度级概率
h = ntrop(f)
p是计算所获得的直方图概率
h就是所计算出的熵
（1）霍夫曼码
概念：哈夫曼编码(Huffman Coding)，又称霍夫曼编码，是一种编码方式，哈夫曼编码是可变字长编码(VLC)的一种。Huffman于1952年提出一种编码方法，该方法完全依据字符出现概率来构造异字头的平均长度最短的码字，有时称之为最佳编码，一般就叫做Huffman编码（有时也称为霍夫曼编码）。通俗来说就是，信源符号出现频率越高，使用的码字就越少。 其过程可以用以下图来进行说明：
编码过程为：
- 对符号的概率进行排序，建立信源递减序列；
- 对每个约简的信源进行编码，从最小的信源开始，一直到原始信源。
在matlab中用函数huffman进行霍夫曼编码，编写代码为：
p = [0.1875 0.5 0.125 0.1875];
c = huffman(p)
celldisp(c)
cellplot(c),title('逻辑单元的单元数组的图像描述')
以递归方式打印单位数组
（2）霍夫曼编码
霍夫曼码的产生不是压缩过程。为了实现成为霍夫曼码的压缩，对于产生码字的符号，不管它们的灰度级、行程长度，还是其他灰度映射操作的输出，都必须在生成码字一致的情况下被变换或映射。
霍夫曼树─即最优二叉树，带权路径长度最小的二叉树，经常应用于数据压缩。 在计算机信息处理中，“霍夫曼编码”是一种一致性编码法（又称“熵编码法”），用于数据的无损耗压缩。
霍夫曼编码的原理： 霍夫曼方法的第一步是通过对所考虑符号的概率进行排序，并将具有最小概率的符号合并为一个符号来替代下次信源化简过程中的符号，从而创建一个简化信源系列。如下图所示那样，载最左边一组虚构的信源符号集合及它们的概率根据概率值的减少从上到下排列，为了形成第一次信源简化，底部的两个概率0.06和0.04进行合并，形成一个概率值为0.1的“复合符号”，这个复合符号及其对应的概率被置于第一个信源简化的列中，以便简化后的信源概率仍然按照其值从大到小进行排列，这个过程一直重复持续到信源只有两个符号的简化信源为止。
检验霍夫曼编码，用软进行实验16字节4×4图像的变长编码映射，编写实验代码：
f2 = uint8([2 3 4 2;3 2 4 4;2 2 1 2;1 1 2 2])
whos('f2')
f2的每个像素都是8比特的字节，16字节表现整幅图像，由于f2的灰度不是等概率的，所以变长码字会减少表现图像所需要的存储量，用函数huffman计算码字：
c= huffman(hist(double(f2(:)),4))
看出与前面的代码获得的码字一样，一般来说，对于任何一幅图像，只要其概率是p = [0.1875 0.5 0.125 0.1875]，计算所得到的码字是一样的。
将f2 二维数组 变换成h1f2 单元数组的转置紧凑显示，代码编写为：
h1f2 = c(f2(:))' %将f2中的元素按照c来查表
whos('h1f2')
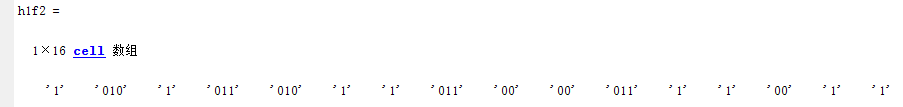
看出其存储空间用了1850个字节，与书上的结果并不一样，是f2要求的存储量的110倍，由于这个存储量太大，要求减少其存储量的开销，因此换成h2f2 字符数组：
h2f2 = char(h1f2)'
whos('h2f2')
h2f2 = h2f2(:);
h2f2(h2f2 == ' ') = [ ];
whos('h2f2')
由于h2f2的存储空间还是比f2的存储大，因此还需要继续压缩，将编码像素打包成单字节：
h3f2 = mat2huff(f2)
whos('h3f2')
结果显示比h2f2的存储量还大，是因为有大部分开销的产生，但这些开销是可以忽略的，将上面的结果进行比率压缩后，得到的结果如下：
hcode = h3f2.code;
whos('hcode')
dec2bin(double(hcode))
这样就实现了霍夫曼编码压缩，其结果所用的存储量比f2初始的存储量小了很多，压缩比接近4：1。
用函数mat2huff进行霍夫曼编码，编写代码如下：
f= imread('C:\Users\Public\Pictures\Sample Pictures\Fig0804(a).tif');
f = im2double(f)
c = mat2huff(f);
cr1 = imratio(f,c)
save SqueezeFig0804(a) c;
cr2 = imratio('C:\Users\Public\Pictures\Sample Pictures\Fig0309(a).tif','SqueezeFig0804(a).mat')
'SqueezeFig0309(a).mat’是MAT-文件，是二进制数据文件，包括工作空间变量名和值。
对比上面的压缩比，看出是不同的，主要差别在matlab数据文件的开销。
（3）霍夫曼译码
经过霍夫曼编码再译码之后，才获得有用的图像，译码器必须计算用来编码x的霍夫曼码，再反映射已编码的数据来重建x，这是一种逆过程，但是缺少了反量化的步骤（这是不可逆转的一步），基本步骤为：
- 从输入结构y中提取维数m和n，以及最小值xmin（最后的输出x）；
- 重建霍夫曼码，通过将它的直方图传递到huffman函数来对x进行编码。在列表中产生的编码将被map调用；
- 建立数据结构（转换和输出表link），以便在y.code中通过一系列有效的二进制搜索对编码数据解码；
- 传递数据结构和已编码数据（如link和y.code）到C函数unravel。这个函数最小化为执行二进制搜索要求的时间，产生已解码的double类的输出向量x；
- 把xmin添加到x的每个元素中，并加以改造以匹配原始x的维数（m行和n列）。
用函数huff2mat来解码是建立一系列的二进制搜素或两个结果解码决策。
function x = huff2mat(y)
if ~isstruct(y) | ~isfield(y, 'min') | ~isfield(y, 'size') | ...
~isfield(y, 'hist') | ~isfield(y, 'code')
error('The input must be a structure as returned by MAT2HUFF.');
end
sz = double(y.size); m = sz(1); n = sz(2);
xmin = double(y.min) - 32768; % Get X minimum
map = huffman(double(y.hist)); % Get Huffman code (cell)
code = cellstr(char('', '0', '1')); % Set starting conditions as
link = [2; 0; 0]; left = [2 3]; % 3 nodes w/2 unprocessed
found = 0; tofind = length(map); % Tracking variables
while length(left) & (found < tofind)
look = find(strcmp(map, code{left(1)})); % Is string in map?
if look % Yes
link(left(1)) = -look; % Point to Huffman map
left = left(2:end); % Delete current node
found = found + 1; % Increment codes found
else % No, add 2 nodes & pointers
len = length(code); % Put pointers in node
link(left(1)) = len + 1;
link = [link; 0; 0]; % Add unprocessed nodes
code{end + 1} = strcat(code{left(1)}, '0');
code{end + 1} = strcat(code{left(1)}, '1');
left = left(2:end); % Remove processed node
left = [left len + 1 len + 2]; % Add 2 unprocessed nodes
end
end
x = unravel(y.code', link, m * n); % Decode using C 'unravel'
x = x + xmin - 1; % X minimum offset adjust
x = reshape(x, m, n); % Make vector an array
将上述编码后的图像进行解码操作，编写代码如下：
load SqueezeFig0804(a);
g = huff2mat(c);
rmse = compare(f,g)
这个结果表明，在霍夫曼编码与霍夫曼解码的过程中均方根误差为0，即原图像和解压后图像之间的均方根误差为0。
（三）空间冗余
概念：图像中相邻像素间的相关性引起的是：空间冗余。空间冗余是图像数据中经常存在的一种数据冗余，是静态图像中存在的最主要的一种数据冗余。同一景物表面上采样点的颜色之间通常存在着空间相关性，相邻各点的取值往往相近或者相同，这就是空间冗余。
f1 = imread('C:\Users\Public\Pictures\Sample Pictures\Fig0807(a).tif');
c1 = mat2huff(f1);
ntrop(f1)
imratio(f1,c1)
subplot(121),imshow(f1),title('原始图像');
subplot(122),imhist(f1),title('其灰度直方图')
f2 = imread('C:\Users\Public\Pictures\Sample Pictures\Fig0807(c).tif');
c2 = mat2huff(f2);
ntrop(f2)
imratio(f2,c2)
subplot(121),imshow(f2),title('原始图像');
subplot(122),imhist(f2),title('其灰度直方图')
由上述两幅图可知，不同的图像可以具有大致相同的直方图和熵，并且其压缩比也大致一样。这些现象表明，变长编码的设计不是为了显示结构间的关系。其实任何一幅图像的像素都可以合理地从它们的相邻像素值预测，这些相关性是像素间冗余的潜在基础。
当图像为RGB彩色图像时，编写实验代码：
f = imread('C:\Users\Public\Pictures\Sample Pictures\Fig0622(a).tif');
f = rgb2gray(f);
subplot(131),imshow(f),title('预测编码原图')
c= mat2huff(f);
ntrop(f)
imratio(f,c)
subplot(122),imhist(f),title('其灰度直方图')
- 为了减少像素间冗余，必须把由人观察和解释的二维像素数组变换为更有效的格式。这种类型的变换被称为映射，当从原始图像可以从变换的数据集重建，它们就被称为可逆映射。
这是映射过程，被称为无损预测编码，其处理方式可以通过对每个像素中新的信息进行提取和编码来消除相近像素间的冗余。新信息被定义为实际值与预测值的差值，公式为：
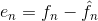
刚刚讨论的是无损预测编码，可以用函数mat2lpc和函数lpc2mat来操作预测编码和解码过程。
运用上面的函数来进行编写代码：
f = imread('C:\Users\Public\Pictures\Sample Pictures\Fig0807(c).tif');
subplot(131),imshow(f),title('预测编码原图')
e=mat2lpc(f);
subplot(132),imshow(mat2gray(e)),title('线性预测编码后的图像');
entropy(e)
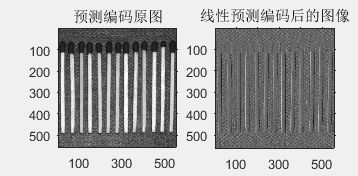
这个熵的数值已经从7.3505比特/像素降低到5.9727比特/像素，意味着预测误差图像可以比原始图像更有效地进行编码。
c =mat2huff(e); %将lpc编码后继续进行huffman编码
cr = imratio(f,c)
[h,x] = hist(e(:)*512,512);
subplot(133),bar(x,h,'k')
g = lpc2mat(huff2mat(c));
imshow(g,[]),title('解码后图')
将解码c与原始图像f进行比较：
RGB彩色图像 预测编码及解码：
f = imread('C:\Users\Public\Pictures\Sample Pictures\Fig0622(a).tif');
f = rgb2gray(f);
subplot(131),imshow(f),title('预测编码原图')
e=mat2lpc(f);
subplot(132),imshow(mat2gray(e)),title('线性预测编码后的图像');
entropy(e)
c =mat2huff(e);
cr = imratio(f,c)
[h,x] = hist(e(:)*512,512);
subplot(133),bar(x,h,'k');
g = lpc2mat(huff2mat(c));
imshow(g,[]),title('解码后图')
compare(f,g)
熵的结果：
压缩比的结果：
彩色图像同理，熵也从7.1638比特/像素减少到4.1246比特/像素，预测误差图像也可以更有效地进行编码，压缩率也从1.1109增大到1.8785。
将解码c与原始图像f进行比较：
实验分析： 无论是灰度图像还是彩色图像变成灰度图像的直方图比较，分别观察图像编码前和解码后图像，发现经过变换后图像均使图像的对比度增强，0周围附近的峰值都很高，这与输入图像的灰度级分布相比有较小的方差，反映的是由预测编码和微分处理除去的像素间冗余。利用预测编码就是对实际值和预值的差（预测误差）进行编码。如果预测比较准确，那么误差信号就会很小，就可以用较少的码位进行编码，以达到数据压缩的目的。
（四）不相关的信息
与编码及像素间冗余不同，心理视觉冗余和真实的或可计量的视觉信息有联系，心理视觉冗余数据的消除引起的定量信息损失很小，成为量化，量化会导致数据的有损压缩。这是一种不可逆操作。就好比一张图像（无法放大）比较小时，人眼是无法直接判断出其分辨率，为了压缩图像的数据量，可以去除一些人眼无法直接观察出的信息，但当其放大时，没有去除心理视觉冗余的图像将和去除心理视觉冗余的图像产生明显差别。
IGS是指改进的灰度级量化，这种方法是认为眼睛对边缘有固有的敏感性，并且可通过对每个像素增加伪随机数来消除，伪随机数在量化前由相邻像素的低阶比特产生。
结合IGS量化的无损预测和霍夫曼编码，代码如下：
f=imread('C:\Users\Public\Pictures\Sample Pictures\Fig0517(a).tif');
q=quantize(f,4,'igs');%用函数quantize进行igs量化到4bit
qs=double(q)/16;
e=mat2lpc(qs); %使用预测编码后
c=mat2huff(e); %再使用霍夫曼编码
imratio(f,c)
subplot(131),imshow(f),title('原始图像');
subplot(132),imshow(e),title('使用预测编码后');
ne=huff2mat(c); %进行霍夫曼解码
nqs=lpc2mat(ne); %图像的一维线性预测解码
nq=16*nqs;
subplot(131),imshow(ne),title('霍夫曼解码');
subplot(132),imshow(nqs),title('线性预测解码');
subplot(133),imshow(nq),title('16倍的线性预测解码')
compare(q,nq)
rmse=compare(f,nq)
这说明解压缩图像的均方根误差大概有七个灰度级，这个误差是由于量化步骤而产生的。
（五）JPEG压缩
前面介绍的在一幅图像的像素上直接操作的技术，这部分讨论一种以修改图像的变换为基础的操作。在变换编码中，一种可逆的类似离散傅里叶变换DFT或离散余弦变换DCT的线性变换如下：
其中，
用一幅图像映射成一组变换系数，然后对它们进行量化和编码。
（1）JPEG
概念：JPEG是Joint Photographic Exports Group的英文缩写，中文称之为联合图像专家小组。该小组隶属于ISO国际标准化组织，主要负责定制静态数字图像的编码方法，即所谓的JPEG算法。这个算法已经成为了大家通用的标准，即 JPEG 标准。JPEG基本编码标准是基于离散余弦变换DCT的，输入和输出图像都被限定在8比特，量化为DCT系数值时限制为11比特。JPEG 压缩是有损压缩，但这个损失的部分是人的视觉不容易察觉到的部分，它充分利用了人眼对计算机色彩中的高频信息部分不敏感的特点，来大大节省了需要处理的数据信息。
ps. jpeg与jpg是基本上一样的，jpg是jpeg的简称。
以下是JPEG的压缩模型示意图，包括编码与解码：
将图像实现jpeg压缩使用函数im2jpeg，此函数内有两个专门的像素块处理函数blkproc和im2col，代码为：
function y = im2jpeg(x, quality)
error(nargchk(1, 2, nargin)); % Check input arguments
if ndims(x) ~= 2 | ~isreal(x) | ~isnumeric(x) | ~isa(x, 'uint8')
error('The input must be a UINT8 image.');
end
if nargin < 2
quality = 1; % Default value for quality.
end
m = [16 11 10 16 24 40 51 61 % JPEG normalizing array
12 12 14 19 26 58 60 55 % and zig-zag redordering
14 13 16 24 40 57 69 56 % pattern.
14 17 22 29 51 87 80 62
18 22 37 56 68 109 103 77
24 35 55 64 81 104 113 92
49 64 78 87 103 121 120 101
72 92 95 98 112 100 103 99] * quality;
order = [1 9 2 3 10 17 25 18 11 4 5 12 19 26 33 ...
41 34 27 20 13 6 7 14 21 28 35 42 49 57 50 ...
43 36 29 22 15 8 16 23 30 37 44 51 58 59 52 ...
45 38 31 24 32 39 46 53 60 61 54 47 40 48 55 ...
62 63 56 64];
[xm, xn] = size(x); % Get input size.
x = double(x) - 128; % Level shift input
t = dctmtx(8); % Compute 8 x 8 DCT matrix
% Compute DCTs of 8x8 blocks and quantize the coefficients.
y = blkproc(x, [8 8], 'P1 * x * P2', t, t');
y = blkproc(y, [8 8], 'round(x ./ P1)', m);
y = im2col(y, [8 8], 'distinct'); % Break 8x8 blocks into columns
xb = size(y, 2); % Get number of blocks
y = y(order, :); % Reorder column elements
eob = max(x(:)) + 1; % Create end-of-block symbol
r = zeros(numel(y) + size(y, 2), 1);
count = 0;
for j = 1:xb % Process 1 block (col) at a time
i = max(find(y(:, j))); % Find last non-zero element
if isempty(i) % No nonzero block values
i = 0;
end
p = count + 1;
q = p + i;
r(p:q) = [y(1:i, j); eob]; % Truncate trailing 0's, add EOB,
count = count + i + 1; % and add to output vector
end
r((count + 1):end) = []; % Delete unusued portion of r
y.size = uint16([xm xn]);
y.numblocks = uint16(xb);
y.quality = uint16(quality * 100);
y.huffman = mat2huff(r);
将压缩过的图像进行解压缩，使用函数jpeg2im进行操作，代码如下：
function x = jpeg2im(y)
error(nargchk(1, 1, nargin)); % Check input arguments
m = [16 11 10 16 24 40 51 61 % JPEG normalizing array
12 12 14 19 26 58 60 55 % and zig-zag reordering
14 13 16 24 40 57 69 56 % pattern.
14 17 22 29 51 87 80 62
18 22 37 56 68 109 103 77
24 35 55 64 81 104 113 92
49 64 78 87 103 121 120 101
72 92 95 98 112 100 103 99];
order = [1 9 2 3 10 17 25 18 11 4 5 12 19 26 33 ...
41 34 27 20 13 6 7 14 21 28 35 42 49 57 50 ...
43 36 29 22 15 8 16 23 30 37 44 51 58 59 52 ...
45 38 31 24 32 39 46 53 60 61 54 47 40 48 55 ...
62 63 56 64];
rev = order; % Compute inverse ordering
for k = 1:length(order)
rev(k) = find(order == k);
end
m = double(y.quality) / 100 * m; % Get encoding quality.
xb = double(y.numblocks); % Get x blocks.
sz = double(y.size);
xn = sz(2); % Get x columns.
xm = sz(1); % Get x rows.
x = huff2mat(y.huffman); % Huffman decode.
eob = max(x(:)); % Get end-of-block symbol
z = zeros(64, xb); k = 1; % Form block columns by copying
for j = 1:xb % successive values from x into
for i = 1:64 % columns of z, while changing
if x(k) == eob % to the next column whenever
k = k + 1; break; % an EOB symbol is found.
else
z(i, j) = x(k);
k = k + 1;
end
end
end
z = z(rev, :); % Restore order
x = col2im(z, [8 8], [xm xn], 'distinct'); % Form matrix blocks
x = blkproc(x, [8 8], 'x .* P1', m); % Denormalize DCT
t = dctmtx(8); % Get 8 x 8 DCT matrix
x = blkproc(x, [8 8], 'P1 * x * P2', t', t); % Compute block DCT-1
x = uint8(x + 128); % Level shift
运用上面两个函数，进行JPEG压缩及解压缩编写实验代码：
f=imread('C:\Users\Public\Pictures\Sample Pictures\Fig0804(a).tif');
c1=im2jpeg(f); %对原始图像f进行jpeg压缩
f1 = jpeg2im(c1); %对压缩后的图像进行解压缩
imratio(f,c1) %计算图像压缩后的压缩比
compare(f,f1,3) %比较两者误差
subplot(121),imshow(f),title('原始图像');
subplot(122),imshow(f1),title('解压缩')
c4 = im2jpeg(f,4); %使用参数4放大归一化数组后的jpeg压缩
f4 = jpeg2im(c4); %解压缩
imratio(f,c4) %比较两者压缩比
compare(f,f4,3)
subplot(121),imshow(f),title('原始图像');
subplot(122),imshow(f4),title('参数为4放大后的解压缩图像')
比较两者误差，显示其直方图和重建图像差别：
实验分析： 对比上面两组图像，看出了放大4倍的jpeg压缩后的图像，比默认值1倍的jpeg压缩图像增加模糊，分辨率变得更低了，产生了棋盘效果，也可以称为块效应。JPEG是一种有损压缩，会把原始数据中不重要的部分去掉，以便可以用更小的体积保存，这是一种牺牲视觉效果而减少存储量的方式。
（2）JPEG2000
概念：JPEG 2000是基于小波变换的图像压缩标准，由Joint Photographic Experts Group组织创建和维护。JPEG 2000通常被认为是未来取代JPEG（基于离散余弦变换）的下一代图像压缩标准。JPEG 2000文件的副档名通常为.jp2，MIME类型是image/jp2。JPEG2000的压缩比更高，而且不会产生原先的基于离散余弦变换的JPEG标准产生的块状模糊瑕疵。JPEG2000同时支持有损压缩和无损压缩。另外，JPEG2000也支持更复杂的渐进式显示和下载。（来自百度百科）
以下是JPEG2000的压缩模型示意图，包括编码与解码：
在JPEG2000编码系统中，通过减去2m-1来进行图像像素灰度级移动，然后计算图像的行和列的一维离散小波变换，在无损压缩中，使用的变换是双正交的，采用的是5-3系数尺度和小波向量；在有损压缩中，使用9-7系数尺度和小波向量。在任何一种情况下，从最初的4个子带的分解中得到图像的低分辨率近似以及图像的水平、垂直和对角线频率特征。
实验中可以使用函数im2jpeg2k进行JPEG2000的编码操作，使用函数jpeg2k2im进行压缩后的解压缩操作。下面对这两种函数进行调用，编写代码如下：
f=imread('C:\Users\Public\Pictures\Sample Pictures\Fig0804(a).tif');
c1=im2jpeg2k(f,5,[8 8.5]); %进行尺度为5变换和分别使用参数8和8.5隐式量化后的图像
f1 = jpeg2k2im(c1); %对压缩后的图像进行解压缩
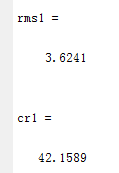
rms1 = compare(f,f1) %误差
cr1 = imratio(f,c1) %两者压缩比
subplot(121),imshow(f),title('原始图像');
subplot(122),imshow(f1),title('解压缩')
c2 = im2jpeg2k(f,5,[8 7]); %进行尺度为5变换和分别使用参数8和7隐式量化后的图像
f2 = jpeg2k2im(c2); %解压缩
rms2 = compare(f,f2)
cr2 = imratio(f,c2)
subplot(121),imshow(f),title('原始图像');
subplot(122),imshow(f2),title('解压缩图像')
c3 = im2jpeg2k(f,1,[1 1 1 1]); %使用显式量化，设四个子带都是步长为1
f3 = jpeg2k2im(c3)
rms3 = compare(f,f3)
cr3 = imratio(f,c3)
subplot(121),imshow(f),title('原始图像');
subplot(122),imshow(f3),title('解压缩图像')
实验分析： 上面两幅图分别是压缩比为42:1和88:1进行编码后产生的重建图像，函数im2jpeg2k只是近似于JPEG2000的算术编码，其压缩率与真的JPEG2000编码器得到的结果是不一样的，真实压缩率会近似地以2的因数增加。我们会发现，当压缩比为42:1时，图像显示的误差降低，变得有些模糊，女士肩部部分产生块效应，但是没有对比压缩比为88:1没有很明显。在88:1压缩比的图像中，女士的眼睛和衣服纹理都被棋盘化，产生“格子”的感觉。在最后一幅图中，使用显式量化，压缩前和解压后的图像基本没有改变，也不会产生棋盘效应，比较好地进行了压缩，但从数据上看，是由于其压缩比较小，误差也较小造成的。因此，实验证明，JPEG和JPEG2000都属于有损压缩。压缩比越大，则解压后的图像损失越大，图像存储所使用的数据量就越小。
（六）视频压缩
说明：视频是图像序列，称为视频帧，其中的每一帧都是单色或者彩色图像。视频压缩存在时间冗余，这是由于相邻帧的像素间相关。
在视频压缩中，可以使用imread('filename.tif',idx)一次一个地读取图像，idx是读入序列中帧的整数索引，为了把非压缩帧写入多帧TIFF文件中，使用imwrite函数来进行操作，imwrite(f,'filename','Compression','none','WriteMode',mode)
其中，当写入初始帧时，mode置为’overmode’；当写入所有的其他帧时置为’append’。注意，imwrite对多帧TIFF文件不提供随机访问支持，帧必须以它们产生的顺序写入。
（1）Matlab图像序列和电影
有两种方法用于在MATLAB中描述视频，分别是：
- 第一种，视频的每一帧都沿着4维数组的第4维连接起来，其结果数组是MATLAB的图像序列，第一二维是行维数和列维数，第三维对于单色图像（或者索引）是1，彩色图像是3，第四维则是图像序列的帧数。
- 第二种，把连续的视频帧插入到称为电影帧的结构矩阵中。
第一种方法编写实验代码：
i = imread('C:\Users\Public\Pictures\Sample Pictures\sky.gif',3); %读取一幅gif类型的彩色图像
frames = size(imfinfo('C:\Users\Public\Pictures\Sample Pictures\sky.gif'),1); %获取图像的具体信息
s1 = uint8(zeros([size(i) 1 2])); % 建立两帧的彩色图像序列
s1(:,:,:,1) = i;
s1(:,:,:,2) = imread('C:\Users\Public\Pictures\Sample Pictures\sky.gif',frames);
size(s1)
以下是原始图像：
第二种描述视频方式，代码如下：
lut = 0:1/255:1;
lut = [lut' lut' lut'];
m1(1) = im2frame(s1(:,:,:,1),lut); %建立第一帧电影帧
m1(2) = im2frame(s1(:,:,:,2),lut); %建立最后一帧电影帧
size(m1) %显示m1的尺寸
m1(1)
可以用implay函数来观看，包括放映、暂停、单步等：
implay(frms,fps) %frms是MATLAB电影或图像序列，fps是回放的帧率(帧每秒),默认是20帧/秒
编写代码如下：
implay(s1,10) %播放s1，且回放帧率是10帧/秒
当需要调整窗口大小以适应播放的图像时，可以滚动条会使得观看区域尺寸增大。
- 需要多帧同时观看时，可以使用函数montage：
montage(frms,'Indices',idxes,'Size',[rows cols]) %idxes是数字数组,用于组装剪辑;rows和rols用于定义形状
编写代码如下：
montage(s1,'Size',[2 1])
下面将一些转换函数进行说明：
- 多帧TIFF文件和MATLAB图像序列之间的转换：
s = tifs2seq('filename.tif') %s是MATLAB图像序列
seq2tifs(s,'filename.tif') %'filename.tif'是多帧TIFF文件
- MATLAB电影和多帧TIFF文件的转换：
m = tifs2movie('filename.tif') %m是MATLAB电影
movie2tifs(m,'filename.tif')
- 多帧TIFF文件与AVI文件的转换：
moive2avi(tifs2moive('filename.tif'),'filename.avi') %'filename.avi'是产生的AVI文件名
（2）时间冗余和运动补偿
从信息论的观点来看，描述信源的数据是信息和数据冗余之和，即：数据=信息+数据冗余。时间冗余是序列图像和语音数据中经常包含的一种数据冗余，这种冗余的产生跟时间紧密相关。时间冗余与空间冗余类似，时间冗余是由于时间上彼此接近的像素相关。
实验代码：
f2 = imread('C:\Users\Public\Pictures\Sample Pictures\Fig0521(a).tif',2);
ntrop(f2)
e2 = mat2lpc(f2); %预测的残留熵
ntrop(e2,512) %预测的残留熵其结果是6.1422
c2 = mat2huff(f2);
imratio(f2,c2) %预测和差值处理的压缩比，比值为1.0960
f1 = imread('C:\Users\Public\Pictures\Sample Pictures\Fig0521(a).tif',1);
ne2 = double(f2) - double(f1);
ntrop(ne2,512) % 预测的残留熵的结果是0
nc2 = mat2huff(ne2);
imratio(f2,nc2) %压缩比是7.9973
使用帧间预测器，让压缩比增加到7.9973。
增加最大帧间预测的准确性的方法是解决帧与帧之间的目标运动——运动补偿 的处理方法。
运动补偿：是一种描述相邻帧（相邻在这里表示在编码关系上相邻，在播放顺序上两帧未必相邻）差别的方法，具体来说是描述前面一帧的每个小块怎样移动到当前帧中的某个位置去。这种方法经常被视频压缩/视频编解码器用来减少视频序列中的空域冗余。它也可以用来进行去交织（deinterlacing）与以及运动插值（motion interpolation）的操作。
运动补偿中的预测编码原理：
帧内编码通常是以宏块为单位的DCT编码，帧间编码是在帧内编码的基础上进行的，在不同帧之间以对应的宏块为对象进行DPCM编码。所谓运动补偿是指对宏块在下一帧的位置做运动估计，将该运动估计用于确定下一帧对应宏块的位置，再进行DPCM编码，使编码考虑了图象的运动分量，即对运动做了补偿，提高编码效率。
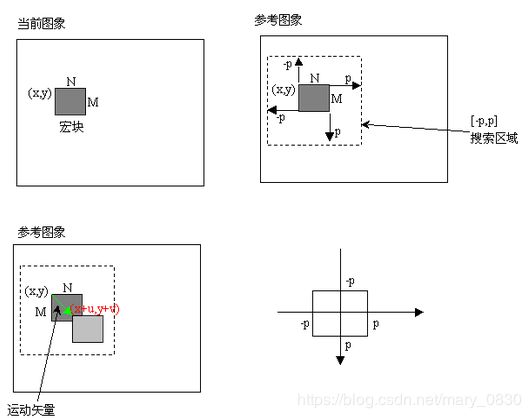
如图所示，对于大小为NxM的宏块的运动估计是在参考图象中一定的范围内寻找最佳的匹配的过程。这种估计方法实际上是假设宏块内部象素具有同样的运动参数，即平滑性约束条件。这只能是一种近似方法，宏块越小平滑性就越好，但运动估计的可靠性也越差，因为匹配时考虑的象素数目就越少，另外寻找最佳匹配的快速算法对较大的宏块比较有效。