目标检测中的样本不平衡处理方法——OHEM, Focal Loss, GHM, PISA
GitHub
简书
CSDN
文章目录
- 1. 前言
- 2. OHEM
- 3. Focal Loss
- 3.1 Cross Entropy
- 3.2 Balanced Cross Entropy
- 3.3 Focal Loss
- 3.4 模型初始化
- 4.GHM(Gradient Harmonizing Mechanism)
- 4.1 Cross Entropy
- 4.2 梯度密度(Gradient Density)
- 4.3 Unit Region Approximation
- 4.4 GHM-R Loss
- 5.PISA
- 5.1 Prime Samples
- 5.2 IoU Hierarchical Local Rank (IoU-HLR)
- 5.3 Learn Detectors via Prime Sample Attention
- 5.3.1 Importance-based Sample Reweighting
- 5.3.2 Classification-Aware Regression Loss
- 6.AP-Loss
- 7.总结
1. 前言
目前。计算机视觉中的性能最好的目标检测方法主要分为两种: one-stage 和two-stage 方法。two-stage方法分为两步,第一步为候选区域生成阶段(Proposal stage),通过如Selective Search、EdgeBoxes等方法可以生成数量相对较小候选目标检测框;第二步为分类与回归阶段,对第一阶段生成的 Candiate Proposal 进行分类和位置回归。one-stage 代表性的方法是R-CNN系列,如 R-CNN, Fast R-CNN, Faster R-CNN。 而one-stage 方法直接对图像的大量 Candiate Proposals 进行分类与回归。
这两类方法中均存在类别不平衡问题,two-stage 方法通过第一步已经将当量的候选区域降低到一个数量较小的范围,同时又在第二步通过一些启发式原则,将正负样本的比例降低到一定程度。而 one-stage 优于没有这降低候选框的步骤,因此,候选区域的数量大大超过 two-stage 方法,因此,在精度上,two-stage 仍然优于 one-stage 方法,但是在速度和模型复杂度上, one-stage 占优势。
类别不平衡会使检测器评估 1 0 4 − 1 0 6 10^4-10^6 104−106 的候选位置,但是通常只有少量的位置存在目标,这回导致两个问题:
- 由于大量的 easy negative 对模型的训练没有提供很大的作用,因此训练很低效;
- 由于在训练中 easy negatives 在数据中占主导,因此这些样本会覆盖少量的正样本的损失(即负样本的损失梯度占主导),从而导致模型退化。
因此,解决样本不平衡问题是提高目标检测精度的一个关键技术之一。
2. OHEM
论文题目:Training Region-based Object Detectors with Online Hard Example Mining
OHEM 是通过改进 Hard Example Mining 方法,使其适应online learning算法特别是基于SGD的神经网络方法。Hard Example Mining 通过交替地用当前样本集训练模型,然后将模型固定,选择 False Positive 样本来重新组建用于下一次模型训练的样本集。但是因为训练神经网络本事就是一个耗时的操作,这样在训练中固定模型,这样会急剧降低模型的训练进程。
Hard Examples Mining通常有两种方法:
-
用于优化 SVM 的方法: 该方法首先需要一个工作的样本集,用来训练 SVM, 使其在该样本集上收敛,然后通过某些原则来添加或删除某些样本以更新该样本集。该原则是:删除那些简单样本(Easy Examples), 即分类正确的概率高与某个阈值(个人理解,原话The rule removes examples that are “easy” in the sense that they are correctly classified beyond the current model’s margin. Conversely), 添加那些困难那样本,即分类正确的概率低于某个阈值(the rule adds new examples that are hard in the sense that they violate the current model’s margin)
-
用于非SVM的方法:该方法首先用完整的数据集中的正样本和一个随机的负样本及来构成开始的训练样本集,然后训练模型使其在该训练集上收敛,然后完整的数据集中选择 False Positive 添加到训练样本集中。
OHEM算法的大致流程是: 首先计算出每个ROI的loss, 然后按loss从高到低来排列每个 ROI, 然后为每张图片选择 B / N B/N B/N 个损失最高的 ROI 作为Hard Examples,其中 B 表示总的 ROI 数量, N N N 表示batch-size 的大小,在 Fast R-CNN 中, N=2, B=128时,效果很好。
但是如果直接按照 loss 对所有的 ROI 进行选择,会有一个缺点,由于 ROI 很多,这样 很多 ROI 的位置就会相关并重叠,如果和某个高 Loss 的 ROI 重合度很高的其它 ROI很多, 这样, 这些 ROI 的 Loss 通常也会很多,这样这些样本都会被选择,但是它们可以近似认为时同一个,这样就会给其它较低 Loss 的 ROI 更少的选择余地,这样就会存在冗余。为了消除这种冗余,作者提出先使用 NMS (non-maximum suppression) 删除部分重合度很高的 ROI, 在使用上述方法进行 选择 Hard Example。
实现技巧:
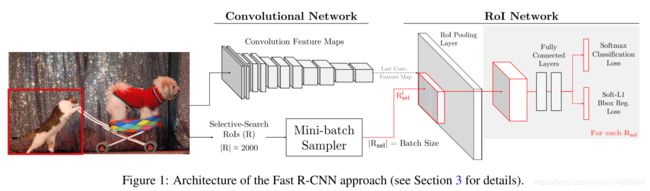
论文,作者将该方法是现在 Fsat R-CNN 目标检测方法中。最简单做法是更改损失函数层,损失函数层首先计算所有 ROI 的 loss, 然后根据 loss 对 ROI 进行排序,并选择 hard RoIs, 让 那些 non-RoIs的损失变为0. 这种方法虽然很简单,但是非常不高效,因为还需要为所有的 RoIs 分配进行反向传播时需要的内存空间。
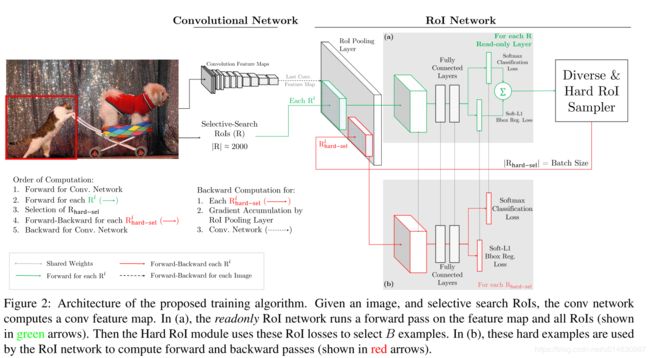
为了克服这个缺点,作者对下面的 Figure 1 进行改进, 如下面的 Figure 2.该改进时使用两份同样的 RoI network。 其中一个是只读的(readonly), 即只进行前向计算,不进行反向传播优化,所以只需要为前向传播分配内存,它的参数实时保持和另一个 RoI network(regular RoI network)保持一样。在每次迭代时,首先使用 readonly RoI network 对每个 ROI 计算起 loss,然后用上面描述的选择 hard RoIs 的方法选择 hard RoIs. 然后利用 regular RoI network来对选择的 hard RoIs 进行前向和后向计算来优化网络。
3. Focal Loss
论文题目 Focal Loss for Dense Object Detection
3.1 Cross Entropy
在改论文中,作者认为样本类别的不平衡可以归结为难易样本的不平衡,从而更改交叉熵损失函数,重新对样本赋予不同的权值,之前的模型这些样本都是同等重要的,从而使模型训练更加关注 hard examples。
首先引入交叉熵的公式:
(公式1) C E ( p , y ) = { − log ( p ) , i f y = = 1 − log ( 1 − p ) , o t h e r w i s e CE(p, y)=\begin{cases} -\log (p), \quad if \quad y == 1 \\ -\log(1-p), \quad otherwise \end{cases} \tag{公式1} CE(p,y)={−log(p),ify==1−log(1−p),otherwise(公式1)
其中, y ∈ { − 1 , 1 } y\in\{-1, 1\} y∈{−1,1},表示真实类别, p ∈ [ 0 , 1 ] p\in[0,1] p∈[0,1]表示我们预测的概率,为了方便,我们定义:
(公式2) p t = { p , i f y = = 1 1 − p , o t h e r w i s e p_t=\begin{cases} p, \quad if \quad y == 1 \\ 1-p, \quad otherwise \end{cases} \tag{公式2} pt={p,ify==11−p,otherwise(公式2)
因此, C E ( p , y ) = C E ( p t ) = − log ( p t ) CE(p,y)=CE(p_t)=-\log(p_t) CE(p,y)=CE(pt)=−log(pt),该方法在 p t p_t pt 较大时,该loss是一个较小的量级, 如下图的连线所示所示,因为存在大量的易分类样本,相加后会淹没正样本的loss。
3.2 Balanced Cross Entropy
一个常见的解决类别不平衡的方式是引入一个加权因子 α ∈ [ 0 , 1 ] \alpha \in [0,1] α∈[0,1] 来表示正样本的权重, 1 − α 1-\alpha 1−α表示负样本的权重。我们按照定义 p t p_t pt 的方法重新定义 α \alpha α为 α t \alpha_t αt, α − b a l a n c e C E l o s s \alpha-balance\quad CE \quad loss α−balanceCEloss 定义如下:
(公式3) C E ( p , y ) = C E ( p t ) = − α t log ( p t ) CE(p,y)=CE(p_t)=-\alpha_t\log(p_t) \tag{公式3} CE(p,y)=CE(pt)=−αtlog(pt)(公式3)
3.3 Focal Loss
α − b a l a n c e C E l o s s \alpha-balance\quad CE \quad loss α−balanceCEloss 虽然可以平衡 positive和negative的重要性,但是对 easy/hard 样本还是无法区分, Focal loss 通过更 Cross loss来达到区分easy/hard的目的:
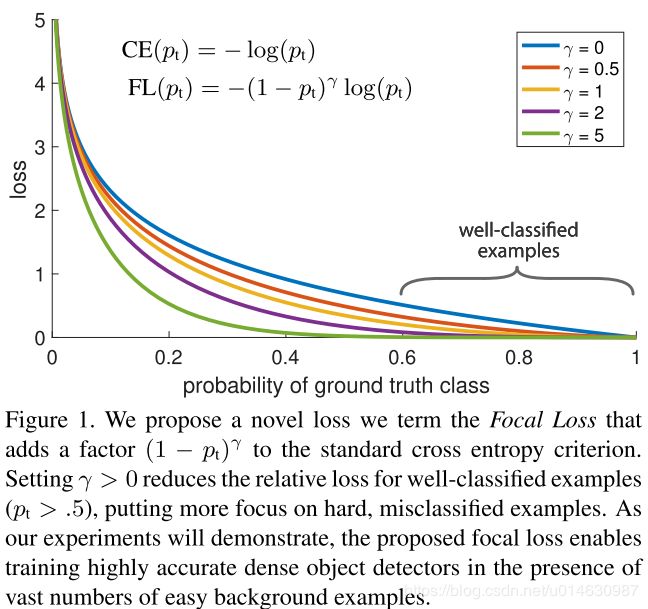
(公式4) F L ( p t ) = − ( 1 − p t ) γ log ( p t ) FL(p_t)=-(1-p_t)^\gamma\log(p_t) \tag{公式4} FL(pt)=−(1−pt)γlog(pt)(公式4)
上图展示了不同 γ \gamma γ 取值对应的 loss,通过分析上述公式,我们发现,当 p t p_t pt 非常小时,即样本被分类错误,此时 ( 1 − p t ) γ (1-p_t)^\gamma (1−pt)γ 接近1, loss几乎不受影响,当 p t p_t pt 接近于1时,即样本被分类正确,此时 ( 1 − p t ) γ (1-p_t)^\gamma (1−pt)γ 接近0,此时降低了该样本的权重,比如,取 γ = 2 \gamma=2 γ=2, 当时 p t = = 0.9 p_t==0.9 pt==0.9时,该样本的 loss 会降低100倍,
在实际应用中,作者使用了该 Focal loss的变体,即加入了 α \alpha α 平衡因子:
(公式5) F L ( p t ) = − α t ( 1 − p t ) γ log ( p t ) FL(p_t)=-\alpha_t(1-p_t)^\gamma\log(p_t) \tag{公式5} FL(pt)=−αt(1−pt)γlog(pt)(公式5)
3.4 模型初始化
作者提出,对于二分类,一般模型的模型初始化会同概率的对待正负样本,由于类别不平衡,负样本的 loss 会占主导,作者提出在训练初始阶段对正样本的概率估计“prior”的概念,用 π \pi π 表示, 通过设置它来达到正样本的输出概率低的效果,比如为0.01,从而使模型更加关注正样本。实际操作中,出了最后一个用于分类的卷积层,其余卷积层的参数初始化为bias b = 0 b=0 b=0 ,而最后一层 b = − log ( ( 1 − π ) / π ) b=-\log((1-\pi)/\pi) b=−log((1−π)/π), 实验中设置为 0.01.
两个实现细节
-
计算 total loss 时,是对一张图片上所有的 ~100k 的anchors 的 focal loss求和,而并不像使用启发式的 RPN 和 OHEM 使用部分小的anchors来计算 loss。 然后通过拥有 gt box 的anchors的数量来进行归一化,不适用所有 anchors 的数量进行归一化的原因是: 由于anchors 存在大量的 easy examples, 因此得到的 Focal loss非常小,如果使用所有 anchors 的数量进行归一化,回导致归一化后的 loss 非常小。
-
当只使用 α \alpha α 时, 将 α \alpha α 偏向样本少的类别,当同时使用 α 和 γ \alpha 和 \gamma α和γ 时,他们需要向相反方向变化,论文中设置为 α = 0.25 , γ = 2 \alpha=0.25,\gamma=2 α=0.25,γ=2.
4.GHM(Gradient Harmonizing Mechanism)
论文题目: Gradient Harmonized Single-stage Detector
改论文提出 Focal Loss 存在两个缺点:
- loss 存在两个超参数,调节该参数是一个费力的操作;
- 该 loss 是一个不会随着数据分布变化而变化的静态 loss。
该论文有一句概括该篇论文的核心思想的一句话: 类别的不平衡可以归结为难易样本的不平衡,难易样本的不平衡可以归结为梯度的不平衡原话如下:
In this work, we first point out that the class imbalance can be summarized to the imbalance in difficulty and the imbalance in difficulty can be summarized to the imbalance in gradient norm distribution.
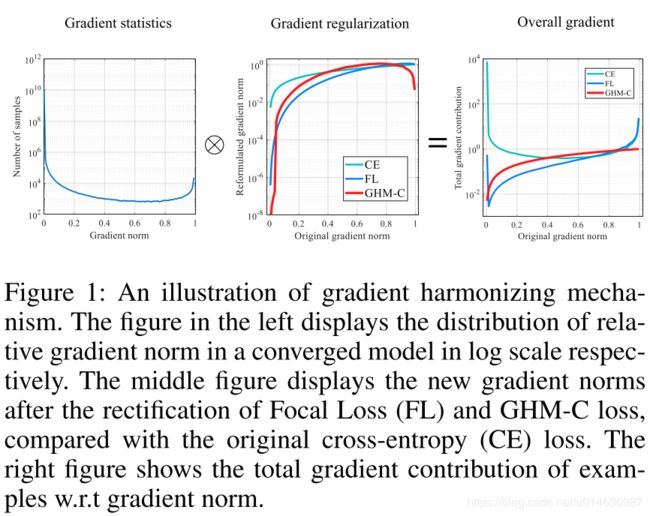
如下图所示:
左边是样本数量关于梯度的分布,中间表示各个修正后的函数的梯度(使用了log scale)对原始梯度的,右边表示所有样本集的梯度贡献的分布。
4.1 Cross Entropy
(公式6) L C E ( p , p ∗ ) = { − log ( p ) , i f p ∗ = = 1 − log ( 1 − p ) , i f p ∗ = = 0 L_{CE}(p, p^*)=\begin{cases} -\log (p), \quad if \quad p^* == 1 \\ -\log(1-p), \quad if \quad p^* == 0 \end{cases} \tag{公式6} LCE(p,p∗)={−log(p),ifp∗==1−log(1−p),ifp∗==0(公式6)
定义 x x x 是模型未经过 sigmoid 之前的输出, 则 p = s i g m o i d ( x ) p = sigmoid(x) p=sigmoid(x),得出该损失函数对 x x x 的梯度为:
(公式7) ∂ L C E ( p , p ∗ ) ∂ x = { p − 1 , i f p ∗ = = 1 p , i f p ∗ = = 0 = p − p ∗ \begin{aligned} \frac{\partial L_{CE}(p, p^*)}{\partial x} &=\begin{cases} p - 1, \quad if \quad p^* == 1 \\ p, \quad if \quad p^* == 0 \end{cases} \\ &= p - p^* \end{aligned} \tag{公式7} ∂x∂LCE(p,p∗)={p−1,ifp∗==1p,ifp∗==0=p−p∗(公式7)
定义梯度的模长(norm) g g g 为:
(公式6) g = ∣ p − p ∗ ∣ = { 1 − p , i f p ∗ = = 1 p , i f p ∗ = = 0 g=|p-p^*|=\begin{cases} 1-p, \quad if \quad p^* == 1 \\ p, \quad if \quad p^* == 0 \end{cases} \tag{公式6} g=∣p−p∗∣={1−p,ifp∗==1p,ifp∗==0(公式6)
4.2 梯度密度(Gradient Density)
训练样本的梯度密度(Gradient Density)定义如下:
(公式7) G D ( g ) = 1 l ϵ ∑ k = 1 N δ ϵ ( g k , g ) GD(g)=\frac{1}{l_\epsilon}\sum_{k=1}^{N}\delta_{\epsilon}(g_k, g) \tag{公式7} GD(g)=lϵ1k=1∑Nδϵ(gk,g)(公式7)
其中, g k g_k gk 是第 k 个样本的gradient norm,
(公式8) δ ϵ ( x , y ) = { 1 , i f y − ϵ 2 ≤ x < y + ϵ 2 0 , i f o t h e r w i s e \delta_{\epsilon}(x, y)=\begin{cases} 1, \quad if \quad y-\frac{\epsilon}{2} \le x < y + \frac{\epsilon}{2} \\ 0, \quad if \quad otherwise \end{cases} \tag{公式8} δϵ(x,y)={1,ify−2ϵ≤x<y+2ϵ0,ifotherwise(公式8)
(公式9) l ϵ ( g ) = m i n ( g + ϵ 2 , 1 ) − m a x ( g − ϵ 2 , 0 ) l_{\epsilon}(g) = min(g+\frac{\epsilon}{2}, 1) - max(g-\frac{\epsilon}{2}, 0) \tag{公式9} lϵ(g)=min(g+2ϵ,1)−max(g−2ϵ,0)(公式9)
这个公式可以理解为,以梯度 g g g 为中心,宽度为 ϵ \epsilon ϵ 的区域内的样本密度。
梯度密度协调参数:
(公式10) β i = N G D ( g i ) = 1 G D ( g 1 ) / N \beta_i=\frac{N}{GD(g_i)} = \frac{1}{GD(g_1)/N} \tag{公式10} βi=GD(gi)N=GD(g1)/N1(公式10)
分母是对梯度位于 g i g_i gi 范围的部分样本进行归一化,如果所有样本的梯度时均分分布,那么对于任意 g i g_i gi 都有 G D ( g i ) = N GD(g_i)=N GD(gi)=N.(这里不是很理解为什么N,可以理解它们相等)
通过将梯度密度协调参数将 GHM 嵌入到损失函数中,则 GHM-C Loss 为:
(公式11) L G H M − C = 1 N ∑ i = 1 N β i L C E ( p i , p i ∗ ) = ∑ i = 1 N L C E ( p i , p i ∗ ) G D ( g i ) \begin{aligned} L_{GHM-C}&=\frac{1}{N}\sum_{i=1}^{N}\beta_iL_{CE}(p_i, p_i^*) \\ &=\sum_{i=1}^{N}\frac{L_{CE}(p_i, p_i^*)}{GD(g_i)} \end{aligned} \tag{公式11} LGHM−C=N1i=1∑NβiLCE(pi,pi∗)=i=1∑NGD(gi)LCE(pi,pi∗)(公式11)
4.3 Unit Region Approximation
计算公式11时,求和有一个N,再求 G D ( g i ) GD(g_i) GD(gi) 时会遍历所有的样本,因此该公式的时间复杂度为 O ( N 2 ) O(N^2) O(N2).如果并行的化,每个计算单元也有N的计算量。对gradient norm进行排序的最好的算法复杂度为 O ( N log N ) O(N\log N) O(NlogN),然后用一个队列去扫描样本得到梯度密度的时间复杂度为 n 。基于排序的方法即使并行也不能较快的计算,因为N往往是 1 0 5 10^5 105 甚至 1 0 6 10^6 106 ,仍然是非常耗时的.
作者提出的近似求解的方法如下:
- 将 g 划分为 M = 1 ϵ M=\frac{1}{\epsilon} M=ϵ1 个单元
- r j = [ ( j − 1 ) ϵ , j ϵ ] r_j=[(j-1)\epsilon, j\epsilon] rj=[(j−1)ϵ,jϵ] 表示第 j 个单元, R j R_j Rj 表示 r j r_j rj 中的样本数量, i n d ( g ) = t ind(g)=t ind(g)=t 表示 g g g 属于第几个 unit。
根据上述定义,得出近似梯度密度函数为:
(公式12) G D ^ ( g ) = R i n d ( g ) ϵ = i n d ( g ) m \hat {GD}(g)=\frac{R _{ind(g)}}{\epsilon}=ind(g)m \tag{公式12} GD^(g)=ϵRind(g)=ind(g)m(公式12)
(公式13) β i ^ = N G D ^ ( g i ) \hat {\beta_i}=\frac{N}{\hat {GD}(g_i)} \tag{公式13} βi^=GD^(gi)N(公式13)
(公式14) L ^ G H M − C = 1 N ∑ i = 1 N β ^ i L C E ( p i , p i ∗ ) = ∑ i = 1 N L C E ( p i , p i ∗ ) G D ^ ( g i ) \begin{aligned} \hat L_{GHM-C}&=\frac{1}{N}\sum_{i=1}^{N}\hat \beta_iL_{CE}(p_i, p_i^*) \\ &=\sum_{i=1}^{N}\frac{L_{CE}(p_i, p_i^*)}{\hat {GD}(g_i)} \end{aligned} \tag{公式14} L^GHM−C=N1i=1∑Nβ^iLCE(pi,pi∗)=i=1∑NGD^(gi)LCE(pi,pi∗)(公式14)
利用上面的公式,由于我们可以事先求好 β ^ \hat \beta β^, 在求和时只需查找 β ^ i \hat \beta_i β^i即可,因此时间复杂度为 O ( M N ) O(MN) O(MN).
因为loss的计算是基于梯度密度函数,而梯度密度函数根据一个batch中的数据得到,一个batch的统计结果是有噪声的。与batch normalization相同,作者用Exponential moving average来解决这个问题,也就是
(公式15) S j ( t ) = α S j ( t − 1 ) + ( 1 − α ) R J ( t ) G ^ D ( g ) = S i n d ( g ) ϵ = S i n d ( g ) M \begin{aligned} S_{j}^{(t)} &= \alpha S_{j}^{(t-1)} + (1-\alpha) R_J^{(t)} \\ \hat GD(g) &= \frac{S_{ind(g)}}{\epsilon} = S_{ind(g)}M \end{aligned} \tag{公式15} Sj(t)G^D(g)=αSj(t−1)+(1−α)RJ(t)=ϵSind(g)=Sind(g)M(公式15)
4.4 GHM-R Loss
将模型鱼的的偏移量定义为 t = ( t x , t y , t w , t h ) t=(t_x, t_y, t_w, t_h) t=(tx,ty,tw,th), 将真实的偏移量定义为 t ∗ = ( t x ∗ , t y ∗ , t w ∗ , t h ∗ ) t^*=(t_x^*, t_y^*, t_w^*, t_h^*) t∗=(tx∗,ty∗,tw∗,th∗),回归loss采用 Smooth L1 loss:
(公式16) L r e g = ∑ i ∈ x , y , w , h S L 1 ( t i − t i ∗ ) L_{reg}=\sum_{i\in{x, y, w, h}}SL_1(t_i-t_i^*) \tag{公式16} Lreg=i∈x,y,w,h∑SL1(ti−ti∗)(公式16)
其中
(公式17) S L 1 ( d ) = { d 2 2 δ i f ∣ d ∣ ≤ δ ∣ d ∣ − δ 2 o t h e r w i s e SL_1(d)=\begin{cases} \frac{d_2}{2\delta} \quad if |d|\le\delta \\ |d|-\frac{\delta}{2} \quad otherwise \end{cases} \tag{公式17} SL1(d)={2δd2if∣d∣≤δ∣d∣−2δotherwise(公式17)
则 L r e g L_{reg} Lreg 关于 d = t i − t i ∗ d=t_i-t_i^* d=ti−ti∗ 的梯度为:
(18) ∂ S L 1 ∂ t i = ∂ S L 1 ∂ d { d δ i f ∣ d ∣ ≤ δ s g n ( d ) o t h e r w i s e \frac{\partial SL_1}{\partial t_i}=\frac{\partial SL_1}{\partial d}\begin{cases} \frac{d}{\delta} \quad if |d| \le \delta \\ sgn(d) \quad otherwise \end{cases} \tag{18} ∂ti∂SL1=∂d∂SL1{δdif∣d∣≤δsgn(d)otherwise(18)
从公式可以看出,当样本操作 ∣ d ∣ |d| ∣d∣ 时, 所有样本都有相同的梯度 1, 这就使依赖梯度范数来区分不同样本是不可能的, 一种简单的替代方法时直接使用 ∣ d ∣ |d| ∣d∣ 作为衡量标准,但是该值理论上无限大,导致 U n i t R e g i o n A p p r o x i m a t i o n Unit Region Approximation UnitRegionApproximation 无法实现,
为了将 GHM 应用到回归损失上,作者修改了原始的 S L 1 SL_1 SL1 损失函数:
(19) A S L 1 ( d ) = d 2 + u 2 − u ASL_1(d) = \sqrt{d_2+u^2}-u \tag{19} ASL1(d)=d2+u2−u(19)
该函数和 S L 1 SL_1 SL1 具有类似的属性,当d的绝对值很小时,近似 L2 loss, 当d的绝对值比较大时, 近似 L1 loss, A S L 1 ASL_1 ASL1 关于d的梯度为:
(20) ∂ A S L 1 ∂ d = d d 2 + u 2 \frac{\partial ASL_1}{\partial d} = \frac{d}{\sqrt{d^2+u^2}} \tag{20} ∂d∂ASL1=d2+u2d(20)
这样就将梯度值限制在 [ 0 , 1 ) [0,1) [0,1)
定义 d r = ∣ d d 2 + u 2 ∣ dr=|\frac{d}{\sqrt{d^2+u^2}}| dr=∣d2+u2d∣, 则 GHM-R Loss 为:
(21) L G H M − R = 1 N ∑ i = 1 N β i A S L 1 ( d i ) = ∑ i = 1 N A S L 1 ( d i ) G D ( g r i ) \begin{aligned} L_{GHM-R}&=\frac{1}{N}\sum_{i=1}^N\beta_i ASL_1(d_i) \\ &=\sum_{i=1}^N\frac{ASL_1(d_i)}{GD(gr_i)} \end{aligned} \tag{21} LGHM−R=N1i=1∑NβiASL1(di)=i=1∑NGD(gri)ASL1(di)(21)
5.PISA
论文题目: Prime Sample Attention in Object Detection
PISA 方法和 Focal loss 和 GHM 有着不同, Focal loss 和 GHM 是利用 loss 来度量样本的难以程度,而本篇论文作者从 mAP 出法来度量样本的难易程度。
作者提出提出改论文的方法考虑了两个方面:
-
样本之间不应该是相互独立的或同等对待。基于区域的目标检测是从大量候选框中选取一小部分边界框,以覆盖图像中的所有目标。因此,不同样本的选择是相互竞争的,而不是独立的。一般来说,检测器更可取的做法是在确保所有感兴趣的目标都被充分覆盖时,在每个目标周围的边界框产生高分,而不是对所有正样本产生高分。作者研究表明关注那些与gt目标有最高IOU的样本是实现这一目标的有效方法。
-
目标的分类和定位是有联系的。准确定位目标周围的样本非常重要,这一观察具有深刻的意义,即目标的分类和定位密切相关。具体地,定位好的样本需要具有高置信度好的分类。
5.1 Prime Samples
Prime Samples 是指那些对检测性能有着巨大影响的样本。作者研究表明样本的重要程度依赖于它和ground truth 的 IoU值,因此作者提出了一种 IOU-HLR 排序。
在目标检测中时如何定义正样本(True Positive)的呢?
- Bouding box 和他最近的 GT 的IoU 大于一个阈值 θ \theta θ;
- 如果该 GT 没有大于阈值的 Bouding Box,则选择最大的 IoU。
剩余的标注为负样本。
mAP 的原理揭露了对目标检测器更重要的两个准则:
-
在所有和gt目标重合的边界框中,IoU最高的边界框时最重要的,因为它的IoU值直接影响召回率。
-
所有不同目标的最高IoU边界框中,具有更高的IoU的边界框更加重要,因为它是随着 θ \theta θ 增加最后一个低于阈值 θ \theta θ 的边界框,从而对整体精度有很大的影响。
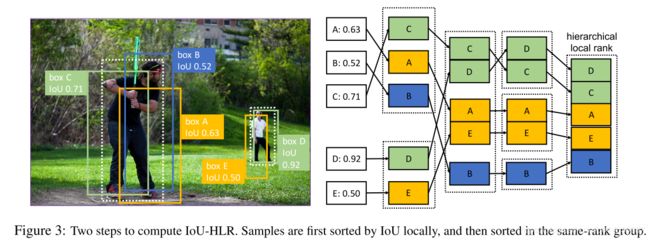
5.2 IoU Hierarchical Local Rank (IoU-HLR)
基于上述分析,作者提出了一种称为 IoU-HLR 的排序方法,它既反映了局部的IoU关系(每个ground truth目标周围),也反映了全局的IoU关系(覆盖整个图像或小批图像)。值得注意的是,不同于回归前的边界框坐标,IoU-HLR是根据样本的最终定位位置来计算的,因为mAP是根据回归后的样本位置来计算的。
该排序方法的大致流程如下图所示,其原理如下:
- 首先将所有的样本根据理他最近的 GT ,将他们分到不同的组;
- 然后在每个组内,按照 IoU对它们进行降序排列,我们得到 IoU Local Rank(IoU-LR);
- 我们对 IoU-LR,进行采样,即将每个组内的TOP1的样本采样出来放在一个组,以此类推对 TOP2, TOP3,一次进行;
- 最后对上面采样的样本,在每个组内进行降序排序,就得到最终的 IoU-HLR.
IoU-HLR遵循上述两个准则。首先,它通过局部排序(即上面的步骤2)将每个单独的 GT 的 对应的样本中 IoU 较高的样本放在前面,其次通过重采样和排序(步骤3, 4)将不同 GT 的 对应的样本中, 将 IoU 较高的放在了前面。
5.3 Learn Detectors via Prime Sample Attention
作者提出Prime Sample Attention,一种简单且有效的采样策略,该采样策略将更多的注意力集中到 Prime examples 上, PISA 由两部分组成: Importance- based Sample Reweighting(ISR)和Classification Aware Regression Loss(为CARL).
PISA 的训练过程是基于 prime samples 而不是同等对待所有样本。
- 首先 prime samples 的权重要大于其他样本的权重, 所以分类往往在这些样本上预测更高的分数;
- 用一个联合目标函数来对分类器和回归其进行学习,因此prime sample的分数相对于不重要样本的分数将会得到提高。
5.3.1 Importance-based Sample Reweighting
作者提出一种基于 soft sampling 的方法: Importance-based Sample Reweighting (ISR), 他给不同样本根据重要性赋予不同的权重。首先它将Iou-HLR排序转化为线性映射的真实值。 IoU-HLR在每个类中分别进行计算。对于类 j j j, 假设总共有 n j n_j nj 个样本, 通过 IoU-HLR 表示为 { r 1 , r 2 , ⋯ , r n j } \{r_1,r_2,\cdots,r_{n_j} \} {r1,r2,⋯,rnj}. 其中 0 ≤ r i ≤ n j − 1 0 \le r_i \le n_j -1 0≤ri≤nj−1,使用一个线性转换函数将 r i r_i ri 转换为 u i u_i ui, 表示第 j j j 类中的第 i i i 个样本的重要程度:
(22) u i = n j − r i n j u_i = \frac{n_j-r_i}{n_j} \tag{22} ui=njnj−ri(22)
采用指数函数的形式来京一部将样本重要性 u i u_i ui 转换为 loss 的权值 w i w_i wi, γ \gamma γ 表示对重要样本给予多大的优先权的程度因子, β \beta β 决定最小样本权值的偏差(感觉就是一个决定最小的权值大小的一个变量)。
(23) w i = ( ( 1 − β ) u i + β ) γ w_i=((1-\beta)u_i + \beta)^\gamma \tag{23} wi=((1−β)ui+β)γ(23)
根据上面得到的权重值,重写交叉熵:
(24) L c l s = ∑ i = 1 n w i ′ C E ( s i , s i ∗ ) + ∑ i = n + 1 m C E ( s i , s i ∗ ) w i ′ = w i ∑ i = 1 n C E ( s i , s i ∗ ) ∑ i = 1 n w i C E ( s i , s i ∗ ) \begin{aligned} L_{cls} &= \sum_{i=1}^{n}w_i^{'}CE(s_i, s_i^*) + \sum_{i=n+1}^{m}CE(s_i, s_i^*) \\ w_i^{'} &= w_i \frac{\sum_{i=1}^{n}CE(s_i, s_i^*)}{\sum_{i=1}^{n}w_iCE(s_i, s_i^*)} \end{aligned} \tag{24} Lclswi′=i=1∑nwi′CE(si,si∗)+i=n+1∑mCE(si,si∗)=wi∑i=1nwiCE(si,si∗)∑i=1nCE(si,si∗)(24)
其中 n 和 m 分别表示真样本和负样本的数量, s i s_i si 和 s i ∗ s_i^* si∗ 分别表示预测分数和分类目标,需要注意的是,如果只是简单的添加 loss 权值将会改变 loss 的值,并改变正负样本的比例,因此为了保持正样本的总的 loss 值不变, 作者将 w i w_i wi 归一化为 w i ′ w_i^{'} wi′
(这里不是很理解,欢迎大家解惑)
5.3.2 Classification-Aware Regression Loss
5.3.1 已经介绍如何染个分类器知道 prime samples, 那么如何让回归其也知道 prime sample,作者提出了 Classification-Aware Regression Loss(CARL) 来联合优化分类器和回归其两个分支。CARL可以提升主要样本的分数,同时抑制其他样本的分数。回归质量决定了样本的重要性,我们期望分类器对重要样本输出更高的分数。两个分支的优化应该是相互关联的,而不是相互独立的。
作者的方法是让回归器知道分类器的分数,这样梯度就可以从回归器传播到分期其分支。公式如下:
(25) L r e g = ∑ i = 1 n c i ′ L ( d i , d ^ i ) c i ′ = c i ∑ i = 1 n L ( s i , s i ∗ ) ∑ i = 1 n c i L ( s i , s i ∗ ) c i = v i 1 n ∑ i = 1 n v i v i = ( ( 1 − b ) p i + b ) k \begin{aligned} L_{reg} &=\sum_{i=1}^n c_i^{'}\mathcal{L}(d_i, \hat d_i) \\ c_i^{'} &= c_i \frac{\sum_{i=1}^{n}\mathcal{L}(s_i, s_i^*)}{\sum_{i=1}^{n}c_i\mathcal{L}(s_i, s_i^*)} \\ c_i &= \frac{v_i}{\frac{1}{n}\sum_{i=1}^{n}v_i} \\ v_i &= ((1-b)p_i +b)^k \end{aligned} \tag{25} Lregci′civi=i=1∑nci′L(di,d^i)=ci∑i=1nciL(si,si∗)∑i=1nL(si,si∗)=n1∑i=1nvivi=((1−b)pi+b)k(25)
p i p_i pi 表示相应类别的预测分数, d i d_i di 表示输出的回归偏移量。利用一个指数函数将 p i p_i pi 转化为 v i v_i vi ,随后根据所有样本的平均值对它进行缩放。为了保持损失规模不变,对具有分类感知的 c i c_i ci 进行归一化。 L \mathcal{L} L 是常用的smooth L1 loss。
L r e g L_{reg} Lreg 关于 c i ′ c_i^{'} ci′ 的梯度与原回归损失 L ( d i , d ^ i ) \mathcal{L}(d_i, \hat d_i) L(di,d^i) 成正比。 $L_{reg} 关于 p i p_i pi 的梯度与 L ( d i , d ^ i ) \mathcal{L}(d_i, \hat d_i) L(di,d^i) 正相关。即回归损失越大的样本分类得分的梯度越大,说明对分类得分的抑制作用越强。从另一个角度看, L ( d i , d ^ i ) \mathcal{L}(d_i, \hat d_i) L(di,d^i) 反映了样本i的定位质量,因此可以认为是一个IoU的估计,进一步可以看作是一个IoU-HLR的估计。可以近似认为,排序靠前的样本有较低的回归损失,于是分类得分的梯度较小。对于CARL来说,分类分支受到回归损失的监督。 不重要样本的得分被极大的抑制掉,而对重要样本的关注得到加强。
6.AP-Loss
待续。。。
7.总结
上面的方法大致可以分为两种:
- Hard Sampling: 从所有样本中选择自己来训练模型: hard negative mining, OHEM
- Soft sampling: 为样本赋予不同的权值: Focal Loss, GHM, PISA
Focal Loss认为正负样本的不平衡,本质上是因为难易样本的不平衡,于是通过修改交叉熵,使得训练过程更加关注那些困难样本,而GHM在Focal Loss的基础上继续研究,发现难易样本的不平衡本质上是因为梯度范数分布的不平衡,和Focal Loss的最大区别是GHM认为最困难的那些样本应当认为是异常样本,让检测器强行去拟合异常样本对训练过程是没有帮助的。PISA则是跳出了Focal Loss的思路,认为采样策略应当从mAP这个指标出发,通过IoU Hierarchical Local Rank (IoU-HLR),对样本进行排序并权值重标定,从而使得recall和precision都能够提升。