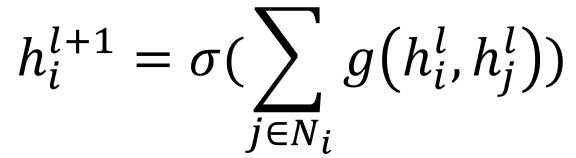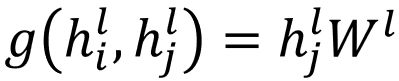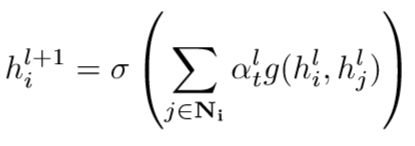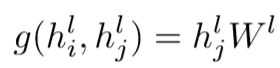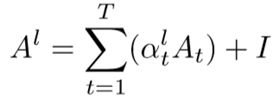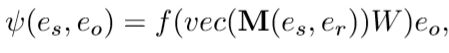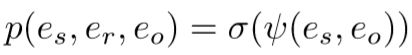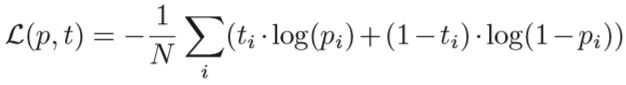为解决知识图谱（KG）中三元组不完整问题，本文结合加权图卷积神经网络（WGCN）和Conv-TransE两个模块，提出了SACN（Structure-Aware Convolutional Networks）模型。SACN通过WGCN来建模KG中的实体和关系，提取实体特征，然后输入至ConvE中使实体满足KG三元组约束，得到实体的embedding表示。通过实验证明，在FB15k-237和WN18RR数据集上超越了之前最佳模型效果的10%，是当前的SOTA模型。
发表于AAAI 2019，作者信息如下：
- 引言
首先简要介绍知识库（Knowledge Base，KB）。知识库中的知识有很多种不同的形式，例如本体知识、关联性知识、规则库、案例知识等。相比于知识库的概念，知识图谱（Knowledge Graph，KG）更加侧重关联性知识的构建。定义KG的主要方法是采用（s, r, o）三元组的形式，举例来说，北京是中国的首都，那么这句话就可以用三元组表示为：(s = Beijing, r = IsCapitalOf, o = China )。其中s称为头实体，r称为关系，o为尾实体。本文的知识库补全任务指的就是知识图谱中三元组的补全。
那么，在有了三元组的定义之后，本文的任务就可以描述为：给定KG，学习实体和关系的嵌入表示，完成三元组补全任务（s, r, o），即给定头实体和关系，求最可能的尾实体。
- 方法
模型的整体框架为WGCN模块提取实体embedding表示，再将实体embedding表示作为Conv-TransE模块的输入，得到满足三元组约束的Loss从而训练整个网络。整体框架如Figure 1所示。
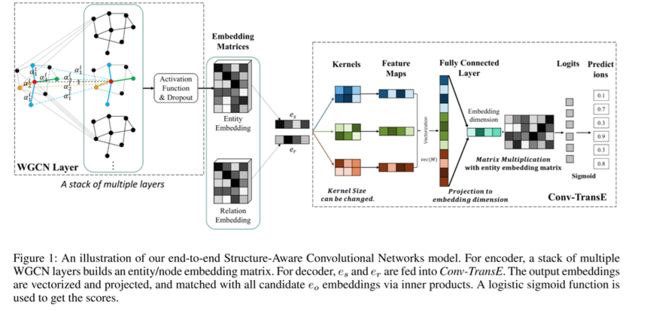下面，本文将按前向传播顺序介绍WGCN和Conv-TransE模块。
1. WGCN
顾名思义，WGCN的全称是Weighted Graph Convolutional Networks，姑且称为加权的图卷积神经网络。其主要思想就是对不同的关系边定义一个不同的权重，将一个多关系图转变为多个带有不同强弱关系的单关系图。构成图的节点为实体，图的边为实体之间的关系。
回忆经典的GCN定义，主要思想为：将每个节点作为聚合的中心节点，对每个中心节点，聚合邻居节点的本层特征表示，来作为中心节点的下一层特征表示，即
其中，Ni表示i节点的邻居节点集合（包括i节点本身），hl为节点在第l层的向量表示。g(·, ·)表示信息传递函数，最基本的定义方法为
通过求和操作，将线性变换后的邻居节点的向量表示共享给中心节点，实现GCN层中的聚合操作。通过GCN层的逐层堆叠，来实现前向传递。值得一提的是，每层GCN都聚合了邻居的信息，在第一层聚合了一阶邻居信息之后，第二层聚合邻居的时候，它的邻居节点已经有了邻居节点的邻居节点的信息，因此第二层GCN聚合了二阶邻居的信息。GCN层堆叠次数越多，中心节点所聚合的邻居范围也越广。更具体的介绍可以查阅文献【1】。
那么我们回到主线，WGCN的与经典GCN的主要区别就是，对知识图谱中的每个关系建模，在聚合过程中给不同的关系以不同的权重。定义权重为αt，1≤t≤T，其中T为关系总数。αt为可学参数。因而前向迭代公式可以写作
其中，g(·, ·)表示信息传递函数，定义同样为
这样，我们将中心节点和邻居节点分离开，可以写作
将其写为矩阵形式，有
其中，At表示第t个关系构成的0-1邻接矩阵，0为无边相连，1为有边相连。因此，形式上就又回到了原始的GCN递推公式【1】
这样我们便将一个多关系图转变成了多个具有不同强弱关系的单关系图，如Figure 2所示，图的右侧分别对应矩阵A、H、W。这便是WGCN的巧妙之处。
另外，关于KG在WGCN中的建图，使用实体作为图的节点，关系作为图的边。值得说明的是，本文还使用了节点的属性作为图的节点，如属性（Tom，gender，male）。这样做的目的是将属性也作为节点，起到“桥”的作用，相同属性的节点可以共享信息。还有作者为了减少过多的属性节点，对节点进行了合并， 将gender也作为了图中的节点，而不是建立male和female两个属性，理由是gender已经能够确定实体的person，而不必过多区分性别。
因此，WGCN同时使用了三元组的结构信息和实体的属性信息，也就是标题中的structure-awared。
2. Conv-TransE
Conv-TransE这个部分类似于ConvE【2】，通过对(s, r)和o进行相似度打分，来预测关系是否成立。与ConvE的主要区别是去掉了ConvE中的reshape操作，具体可以参看文献【2】。这里给出经典的KG表征学习的打分函数。
来看模型结构，如图所示。
举例来说，将WGCN得到的实体s的embedding和预训练的关系r的embedding进行concat操作，变成一个2*n维的矩阵。对这个矩阵进行卷积操作，通过多个相同尺寸的卷积核，得到feature maps。然后将feature maps拉直成一个向量，通过全连接层进行维度缩减。将这个融合了s和r的向量与WGCN生成的所有向量分别进行点积操作，计算（s，r）与所有待选o的相似度。相似度通过sigmoid缩放到0~1范围内，取相似度最高的作为预测的实体o。
打分函数（相似度函数）体现了前向传播的过程，公式形式为
M(·, ·)表示卷积操作，vec(·)表示拉直操作，f(·)为激活函数。
将打分函数通过sigmoid函数，得到（s, r）和待选o构成三元组成立的概率，即
因此，整个网络的损失也就可以定义为，（s, r）和待选o构成三元组是否成立的二分类交叉熵，即
- 数据集
文中共使用了三个数据集，包括：
1）FB15k-237: freebase三元组
2）WN18RR: wordnet三元组
3）FB15k-237-Attr:作者从FB24k中抽取了实体的属性
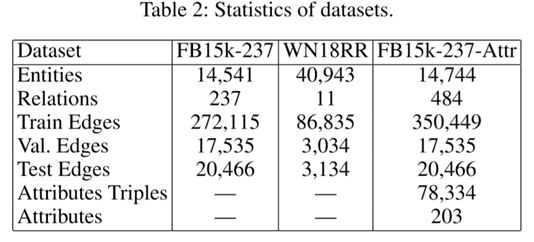
具体的统计信息如下：
- 实验
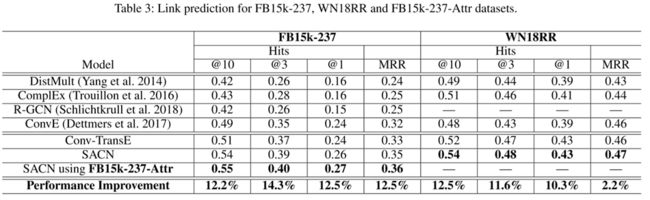
文章进行了链接预测任务的实验，实验结果如表3。可以看到，带有属性节点的SACN性能表现达到了State-Of-The-Art。
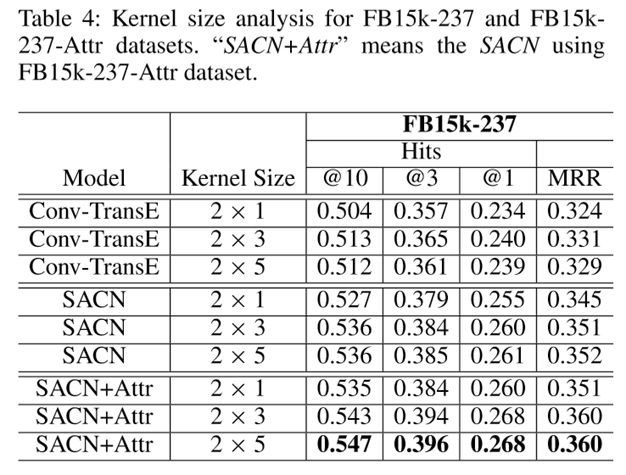
参数敏感性部分，文章尝试了不同长度的卷积核，针对不同的数据集有不同的最优参数。
文章还对不同的度的节点的性能进行了比较，可以看到，在度较低的节点下是SACN高于Conv-TransE的，因为邻居节点可以共享更多的信息；然而度较高的节点则效果不如单独的Conv-TransE，文章对它的解释是较多的邻居节点使较重要的邻居信息被过度“平滑”掉了，因此比不上单纯的Conv-TransE。
- 结束语
作者用WGCN来捕获具有相关关系的实体特征，使邻居节点的信息得以共享，这样学到的实体表示要好于孤立的学习ConvE得到的实体表示。本质上是GCN+ConvE的模型框架，这种串联的框架对其他类似的任务也有启发性。另外的体会是深度学习方面的研究，还是要多读论文多总结。好的，做完了这篇博客，相信事情总可以一件一件一件的做完！
参考文献
【1】Kipf, T.N., & Welling, M. (2016). Semi-Supervised Classification with Graph Convolutional Networks. ArXiv, abs/1609.02907.
【2】Dettmers, T., Minervini, P., Stenetorp, P., & Riedel, S. (2017). Convolutional 2D Knowledge Graph Embeddings. AAAI.