数据挖掘_task1赛题分析

1.理解赛题

赛题：零基础入门数据挖掘 - 二手车交易价格预测

1.1 赛题要求

比赛要求参赛选手根据给定的数据集，建立模型，二手汽车的交易价格。
来自 Ebay Kleinanzeigen 报废的二手车，数量超过 370,000，包含 20 列变量信息，为了保证 比赛的公平性，将会从中抽取 10 万条作为训练集，5 万条作为测试集 A，5 万条作为测试集 B。同时会对名称、车辆类型、变速箱、model、燃油类型、品牌、公里数、价格等信息进行 脱敏。
赛题分析

1. 此题为传统的数据挖掘问题，通过数据科学以及机器学习深度学习的办法来进行建模得到结果。
2. 此题是一个典型的回归问题。
3. 主要应用xgb、lgb、catboost，以及pandas、numpy、matplotlib、seabon、sklearn、keras等等数据挖掘常用库或者框架来进行数据挖掘任务。
4. 通过EDA来挖掘数据的联系和自我熟悉数据。

赛题分析：主要是了解题目是分类问题还是回归问题，用什么模型可能效果较好，评价指标是什么？

1.2 数据

一般而言，对于数据在比赛界面都有对应的数据概况介绍（匿名特征除外），说明列的性质特征。了解列的性质会有助于我们对于数据的理解和后续分析。 Tip:匿名特征，就是未告知数据列所属的性质的特征列。

**train.csv**
* name - 汽车编码
* regDate - 汽车注册时间
* model - 车型编码
* brand - 品牌
* bodyType - 车身类型
* fuelType - 燃油类型
* gearbox - 变速箱
* power - 汽车功率
* kilometer - 汽车行驶公里
* notRepairedDamage - 汽车有尚未修复的损坏
* regionCode - 看车地区编码
* seller - 销售方
* offerType - 报价类型
* creatDate - 广告发布时间
* price - 汽车价格
* v_0', 'v_1', 'v_2', 'v_3', 'v_4', 'v_5', 'v_6', 'v_7', 'v_8', 'v_9', 'v_10', 'v_11', 'v_12', 'v_13','v_14'（根据汽车的评论、标签等大量信息得到的embedding向量）【人工构造 匿名特征】
　
 
数字全都脱敏处理，都为label encoding形式，即数字形式

1.2.1 预测指标

1.2.1常见评价指标
分类算法常见的评估指标如下：

• 对于二类分类器/分类算法，评价指标主要有accuracy， [Precision，Recall，F-score，Pr曲线]，ROC-AUC曲线。
• 对于多类分类器/分类算法，评价指标主要有accuracy， [宏平均和微平均，F-score]。

二类分类器：
准确率(accuracy)：准确率是我们常见的评价指标之一，一般定义是，分类正确的样本数占总样本的比例数。

二分类问题的预测结果可以根据情况分成以下四类：

真正例（True Positive）：预测值为1，真实值为1

假正例（False Positive）：预测值为1，真实值为0

真反例（True Negative）：预测值为0，真实值为0

假反例（False Negative）：预测值为0，真实值为1

精准率可以解释为，预测为正例的样本中，有多少是真的正例。

召回率可以解释为，真实的正例的样本中，有多少被预测出来。
F-score 精准率和召回率的调和平均

AUC是另一种评价二分类算法的指标，被定义为 ROC 曲线下的面积。

ROC曲线的坐标，纵坐标为真正例率（True Positive Rate,TPR），横坐标为假正例率（False Positive Rate,FPR）

AUC参考：https://blog.csdn.net/pzy20062141/article/details/48711355
多类分类器

宏平均（Macro-averaging），是先对每一个类统计指标值，然后在对所有类求算术平均值。把所有类的F1值取一个算术平均就得到了Macro-average

微平均（Micro-averaging），是对数据集中的每一个实例不分类别进行统计建立全局混淆矩阵，然后计算相应指标

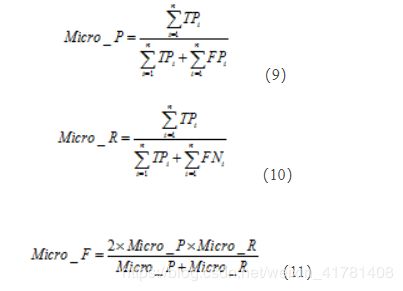
例子：

考虑现在输入分类器的样本有10个，他们属于类别A B C

假设这10个样本的真实类标为（有序）和分类器预测的类标分别是：

真实：A A A C B C A B B C
预测：A A C B A C A C B C
precision(A) = 3(正确预测为A类的样本个数为3) / 4(预测为A类的样本数为4) = 0.75 recall(A) = 3 / 4(真实A类样本有4个) = 0.75

precision(B) = 1 / 2 = 0.5 recall(B) = 1 / 3 = 0.3333

precision(C) = 2 / 4 = 0.5 recall(C) = 2 / 3 = 0.6667

F值计算出来之后，取算术平均就是Macro-average

Micro-average = 6(预测正确的样本个数) / 10 = 0.6

对于回归预测类常见的评估指标如下:

• 平均绝对误差（Mean Absolute Error，MAE），均方误差（Mean Squared Error，MSE），平均绝对百分误差（Mean Absolute Percentage Error，MAPE），均方根误差（Root Mean Squared Error）， R2（R-Square）

平均绝对误差
平均绝对误差（Mean Absolute Error，MAE）:平均绝对误差，其能更好地反映预测值与真实值误差的实际情况，其计算公式如下：
$$MAE=\frac{1}{N}\sum _{i=1}^N\left|y_i-{\hat{y}}_i\right|$$

均方误差
均方误差（Mean Squared Error，MSE）,均方误差,其计算公式为：
$$MSE=\frac{1}{N}\sum _{i=1}^N{\left(y_i-{\hat{y}}_i\right)}^2$$

R2（R-Square）的公式为：
残差平方和：
$$S{S}_{res}=\sum {\left(y_i-{\hat{y}}_i\right)}^2$$
总平均值:
$$S{S}_{tot}=\sum {\left(y_i-{\overline{y}}_i\right)}^2$$

其中$\overline{y}$表示$y$的平均值
得到$R^2$表达式为：
$$R^2=1-\frac{S{S}_{res}}{S{S}_{tot}}=1-\frac{\sum {\left(y_i-{\hat{y}}_i\right)}^2}{\sum {\left(y_i-\overline{y}\right)}^2}$$
$R^2$用于度量因变量的变异中可由自变量解释部分所占的比例，取值范围是 0~1，$R^2$越接近1,表明回归平方和占总平方和的比例越大,回归线与各观测点越接近，用x的变化来解释y值变化的部分就越多,回归的拟合程度就越好。所以$R^2$也称为拟合优度（Goodness of Fit）的统计量。

$y_i$表示真实值，${\hat{y}}_i$表示预测值，${\overline{y}}_i$表示样本均值。得分越高拟合效果越好。

本赛题的评价标准为MAE(Mean Absolute Error):

$$MAE=\frac{{\sum }_{i=1}^n\left|y_i-{\hat{y}}_i\right|}{n}$$
其中$y_i$代表第$i$个样本的真实值，其中${\hat{y}}_i$代表第$i$个样本的预测值。

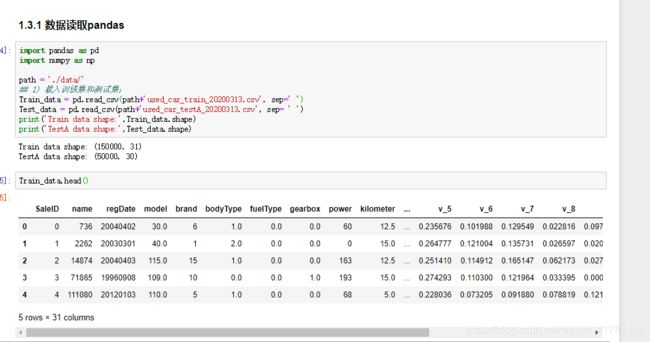
1.3 读取数据代码

1.4 查看一些pandas 自带对数据得统计

参考：https://tianchi.aliyun.com/competition/entrance/231784/introduction?spm=5176.12281957.1004.1.38b02448ausjSX
https://www.cnblogs.com/robert-dlut/p/5276927.html

https://www.jiqizhixin.com/articles/2019-03-07-12

https://www.plob.org/article/20575.html