【PyTorch入门】之一文看懂多层感知机(ML)【附 绘制激活函数图像的程序】
先打个广告哈。我自己做的公众号【拇指笔记】,每天写写我自己学习中记下的笔记,欢迎各位大神关注一下~
本篇文章完整程序可以在我的公众号后台回复"APF"获取,欢迎各位关注!
1. 多层感知机(MLP)
本节将以多层感知机为例,介绍多层神经网络的概念。
1.1 隐藏层
下图为一个多层感知机的神经网络图。
多层感知机在单层神经网络的基础上引入了一到多个隐藏层(hidden layer)。如图所示的隐藏层一共有5个隐藏单元。由于输入层不涉及计算,因此这个多层感知机的层数为2。如图所示的多层感知机中的隐藏层和输出层都是全连接层。
对于一个只有一个隐藏层且隐藏单元个数为 h h h的多层感知机,记它的输出为 H H H。因为这个多层感知机中的隐藏层和输出层都是全连接层,所以可以设:隐藏层的权重参数和偏差参数分别为 W h W_h Wh和 b h b_h bh,输出层的权重参数和偏差参数分别为 W o W_o Wo和 b o b_o bo
由此我们可以得到单隐藏层神经网络输入、隐藏层输出和输出之间的关系
H = X W h + b h O = H W o + b o H = XW_h+b_h \\O = HW_o+b_o H=XWh+bhO=HWo+bo
将两个式子联立起来,得到输入与输出之间的关系。
O = ( X W h + b h ) W o + b o = X W h W o + b h W o + b o O = (XW_h+b_h)W_o+b_o \\ =XW_hW_o+b_hW_o+b_o O=(XWh+bh)Wo+bo=XWhWo+bhWo+bo
由式(2)不难看出,这样的神经网络虽然引入了(一个或多个)隐藏层,却依然等价于一个单层神经网络。引起该问题的根源是全连接层,全连接层只是对数据进行仿射变换,而多个仿射变换叠加仍然为一个仿射变换。为了解决这样的问题,引入了非线性变换,即激活函数。
1.2 激活函数
非线性函数是指对隐藏变量使用暗元素运算的非线性函数进行变换,然后再做为下一个全连接层输入。这个非线性函数叫做激活函数。
下面介绍几种常用的激活函数。
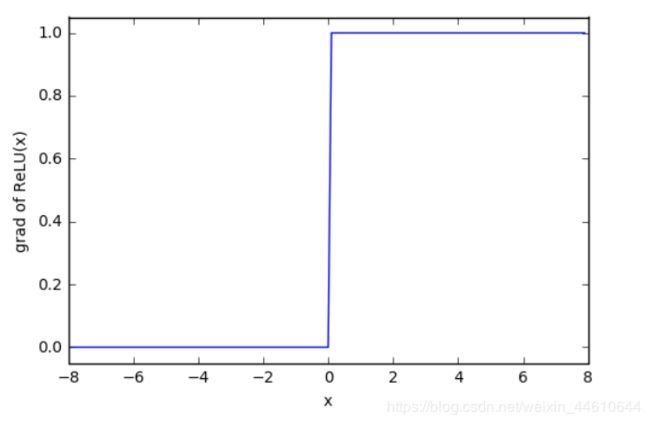
1.2.1 ReLU函数(线性整流函数)
ReLU函数
-
功能: ReLU函数只保留正数元素,并将负数元素清零。
-
定义:
R e L U ( x ) = m a x ( x , 0 ) ReLU(x) = max(x,0) ReLU(x)=max(x,0)
- 函数图像和导数图像:
- 绘制程序
# 老板关注下公众号给点鼓励呗
%matplotlib inline
import torch
import numpy as np
import matplotlib.pylab as plt
x = torch.arange(-8.0, 8.0, 0.1, requires_grad=True)
y = x.relu()
y.sum().backward()
z = x.grad
x = x.detach().numpy()
y = y.detach().numpy()
plt.ylim(ymin=-1,ymax=7)
plt.plot(x, y)
plt.xlabel('x')
plt.ylabel('ReLU(x)')
plt.figure(2)
plt.ylim(ymin=-0.05,ymax=1.05)
plt.xlim(xmin=-8,xmax=8)
plt.plot(x,z)
plt.xlabel('x')
plt.ylabel('grad of ReLU(x)')
1.2.2 sigmoid函数(S型函数)
sigmoid函数
- 功能: sigmoid函数可以将元素的值变换到0和1之间。
- 定义:
s i g m o i d ( x ) = 1 1 + e x p ( − x ) sigmoid(x)=\frac{1}{1+exp(-x)} sigmoid(x)=1+exp(−x)1
- 函数图像和导数图像:
- 绘制程序
# 老板关注下公众号给点鼓励呗
%matplotlib inline
import torch
import numpy as np
import matplotlib.pylab as plt
x = torch.arange(-8.0, 8.0, 0.1, requires_grad=True)
y = x.sigmoid()
y.sum().backward()
z = x.grad
x = x.detach().numpy()
y = y.detach().numpy()
plt.ylim(ymin=-0.1,ymax=1.1)
plt.plot(x, y)
plt.xlabel('x')
plt.ylabel('sigmoid(x)')
plt.figure(2)
plt.ylim(ymin=-0.05,ymax=0.3)
plt.xlim(xmin=-8,xmax=8)
plt.plot(x,z)
plt.xlabel('x')
plt.ylabel('grad of sigmoid(x)')
1.2.3 tanh函数(双曲正切函数)
tanh函数
- 功能:可以将元素的值变换到-1和1之间
- 定义:
t a n h ( x ) = 1 − e x p ( − 2 x ) 1 + e x p ( − 2 x ) tanh(x) =\frac{1-exp(-2x)}{1+exp(-2x)} tanh(x)=1+exp(−2x)1−exp(−2x)
- 函数图像和导数图像
- 绘制程序
# 老板关注下公众号给点鼓励呗
%matplotlib inline
import torch
import numpy as np
import matplotlib.pylab as plt
x = torch.arange(-8.0, 8.0, 0.1, requires_grad=True)
y = x.tanh()
y.sum().backward()
z = x.grad
x = x.detach().numpy()
y = y.detach().numpy()
plt.ylim(ymin=-1.1,ymax=1.1)
plt.plot(x, y)
plt.xlabel('x')
plt.ylabel('tanh(x)')
plt.figure(2)
plt.ylim(ymin=-0.05,ymax=1.1)
plt.xlim(xmin=-8,xmax=8)
plt.plot(x,z)
plt.xlabel('x')
plt.ylabel('grad of tanh(x)')
1.3 多层感知机(MLP)
多层感知机就是含有至少一个隐藏层的由全连接层组成的神经网络,且每个隐藏层的输出通过激活函数进行变换 。多层感知机的层数和各隐藏层中隐藏单元个数都是超参数。
H = ϕ ( X W h + b h ) O = H W o + b o 式 中 ϕ 表 示 激 活 函 数 H = \phi(XW_h+b_h) \\O = HW_o+b_o \\式中\phi表示激活函数 H=ϕ(XWh+bh)O=HWo+bo式中ϕ表示激活函数
通过对输出层进行操作,我们可以将多层感知机和之前的线性回归模型及softmax回归模型相结合。