FPGA面试笔试专题——一些基础电路设计

 

1、全加器设计

全加器考虑进位输入与进位输出，以4位全加器为例：

module full_add(
input rst_n,
input clk,
input [3:0]a,
input [3:0]b,
input cin,
output reg [3:0]sum,
output reg cout
);

always@(posedge clk or negedge rst_n)
begin
    if(!rst_n)
        begin
            {cout,sum} <= 5'b0;
        end
    else
        begin
            {cout,sum} <= a+b+cin;
        end
end
endmodule

2、4选1数据选择器

按照组合逻辑实现，可以使用case语句（应注意case的语法）：

module choose41(
input a1,
input a2,
input a3,
input a4,
input [1:0]sel,
output reg c
);

always@(*)
begin
    case(sel)
    2'b00:begin
            c = a1;
        end
    2'b01:begin
            c = a2;
        end
    2'b10:begin
            c = a3;
        end
    2'b11:begin
            c = a4;
        end
    default:begin
            c = a1;
        end

end

3 、译码器

译码器将输入编码转换为对应输出，以3_8译码器为例：

module decode3_8(
input en,
input [2:0]code,
output reg[7:0]state,
);

always@(*)
begin
    if(!en)
        begin
            state <= 8'd0;
        end
    else
        begin
            case(code)
            3'b000:begin
                state = 8'b0000_0001;
            end
            3'b001:begin
                state = 8'b0000_0010;
            end
            3'b010:begin
                state = 8'b0000_0100;
            end
            3'b011:begin
                state = 8'b0000_1000;
            end
            3'b100:begin
                state = 8'b0001_0000;
            end
            3'b101:begin
                state = 8'b0010_0000;
            end
            3'b110:begin
                state = 8'b0100_0000;
            end
            3'b111:begin
                state = 8'b1000_0000;
            end
            default:begin
                state = 8'b0000_0000;
            end
            endcase
        end
end
endmodule

4、计数器

计数器比较简单，此处重点在于回顾parameter的使用；设计一个模值任意的计数器；

module cnt
#(parameter W = 4,C = 2<<(W-1))
(
input clk,
input rst_n,
output reg[C-1:0]cnt
);

always@(posedge clk or negedge rst_n)
begin
    if(!rst_n)
        begin
            cnt <= W'd0;
        end
    else
        begin
            if(cnt==C-1)
                begin
                    cnt <= W'd0;
                end
            else
                begin
                    cnt <= cnt+1'b1;
                end
        end
end
endmodule

5、模为60的BCD码计数器

BCD码计数器与普通２进制计数器不同，

module cntBCD_60(
input clk,
input rst_n,
output reg [7:0]cnt 
);

always@(posedge clk or negedge rst_n)
begin
    if(!rst_n)
        begin
            cnt <= 8'd0;
        end
    else 
        begin
            if(cnt[3:0]==4'd9)
                begin
                    cnt[3:0] <= 4'd0;
                    if(cnt[7:4]==4'd5)
                        begin
                            cnt[7:4] <= 4'd0;
                        end
                    else
                        begin
                            cnt[7:4] <= cnt[7:4]+1'b1;
                        end
                end
            else
                begin
                    cnt[3:0] <= cnt[3:0]+1'b1;
                end
        end
end
endmodule

6、两数乘法

乘法的本质就是移位，因此可以通过循环移位与求和实现，以8位数相乘为例：

module multy(
input [7:0]a,
input [7:0]b,
output [15:0]c
);
integer i;
always@(*)
begin
    c = 16'd0;
    for(i=0;i<8;i=i+1)
        begin
            if(a[i]) c = c + (a<

应注意：

• 输出的位宽为输入之和
• for循环必须在always块中
• for()中为；而不是，

用repeat应该也能实现相同功能：

module multy(
input [7:0]a,
input [7:0]b,
output [15:0]c
);
integer i;
always@(*)
begin
    c = 16'd0;
    i = 0;
    repeat(8)
        begin
            if(a[i]) c = c + (a<

7、调用门元件实现4选1 MUX

调用门原件实现电路，实际上就是结构化描述电路（数据流、行为级抽象层次更高，不关心具体电路实现）

module Mux4_1(
input a,
input b,
input c,
input d,
input sel1,
input sel0,
output out
);

wire a1,b1,c1,d1;
wire sel1_n,sel0_n;

NOT (sel1_n,sel1);
NOT (sel0_n,sel0);

AND (a1,sel1_n,sel0_n，a);
AND (b1,sel1_n,sel0,b);
AND (c1,sel1,sel0_n,c);
AND (d1,sel1,sel0,d);


OR (out,a1,b1,c1,d1);

endmodule

其行为级描述为：

 assign out = (a & ~cont1 & ~cont2)| (b & ~cont1 & cont2)| (c & cont1 & ~cont2)| (d & cont1 & cont2);  

8、环形计数器

环形计数器实际就是循环右移寄存器，因此N位环形计数器有N个状态（N位计数）;

以8位环形计数器为例：

module hcnt(
input rst_n,
input clk,
output reg [7:0]out
);
always@(posedge clk or negedge rst_n)
begin
    if(!rst_n)
        out <= 8'd0;
    else
        out <= {out[0],out[7:1]};
end
endmodule

9、扭环形计数器

环形计数器也是由循环右移寄存器构成，与环形计数器不同的是最低位取反后移到最高位，因此N位环形计数器有2N个状态（2N位计数）;

以8位扭环形计数器为例：

module ncnt(
input rst_n,
input clk,
output reg [7:0]out
);
always@(posedge clk or negedge rst_n)
begin
    if(!rst_n)
        out <= 8'd0;
    else
        out <= {~out[0],out[7:1]};
end
endmodule

10、使用一个二选一MUX和一个INV实现异或

由异或逻辑可以知道，out = ~a&b + a&~b;

即：a=0时，out = b；

a=1时，out = ~b；

因此电路可以设计为：

assign out = a?~b:b;

其中，a作为MUX的选择信号，b与~b（INV实现）作为MUX输入。

11、利用4选1实现F(x,y,z)=xz+yz'  

从真值表入手：

	xy=00	xy=01	xy=10	xy=11
z=0	0	1	0	1
z=1	0	0	1	1

进一步化简：

	xy=00	xy=01	xy=10	xy=11
out	0	~z	z	1

可以看出4选1实现逻辑：

always@(*)
begin
    case({x,y})
    2'b00:begin
        out = 1'b0;
    end
    2'b01:begin
        out = ~z;
    end
    2'b10:begin
        out = z;
    end
    2'b11:begin
        out = 1'b1;
    end
    default:begin
        out = 1'b0;
    end
    endcase
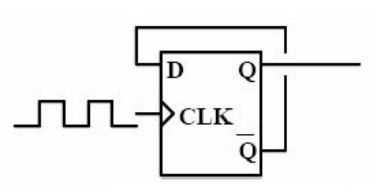
end

12、利用D触发器实现2分频