数学建模【图与网络模型(图的基本概念与数据结构、最短路-最小生成树-网络最大流问题、Matlab图论工具箱、渡河问题、钢管的订购与运输)】

【学习网址：MOOC---郑州轻工业大学---数学建模与实验】数学建模专栏

• 笔记01【第1、2章】【概述、软件介绍】
• 笔记02【第3章】【数据处理方法】
• 笔记03【第4章】【规划模型】
• 笔记04【第5章】【图与网络模型】
• 各个章节---作业题解析

目   录

5.1 图的基本概念与数据结构

5.1.1 图的基本概念

5.1.2 图与网络的数据结构

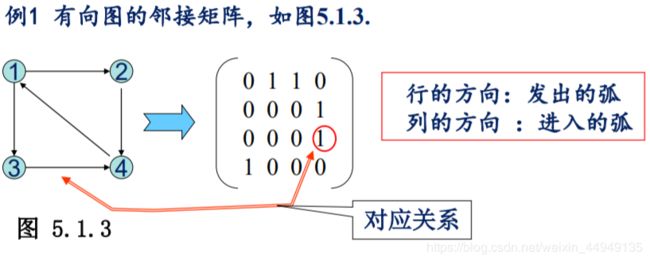
1.邻接矩阵表示法

2.稀疏矩阵表示法

5.2 最短路问题

5.2.1 问题描述

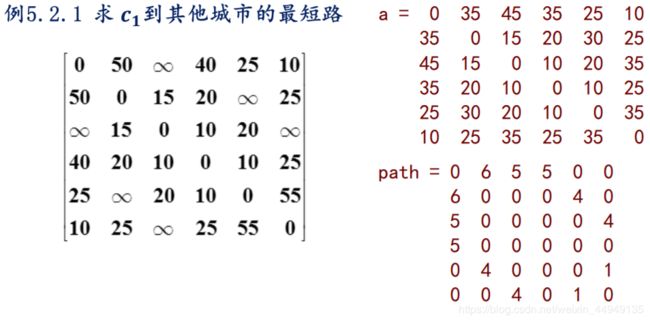
例5.2.1 求c1到其他城市的最短路

5.2.2 两指定顶点间的最短路径模型

例5.2.1 求c1到其他城市的最短路

5.2.3 每对顶点间的最短路径

例5.2.1 求c1到其他城市的最短路

5.3 最小生成树问题

5.3.1 生成树

5.3.2 最小生成树

1.Prim算法

2. Kruskal算法

5.4 网络最大流问题

5.4.1 基本概念

1.网络与流

2.可行流与最大流

3.增广路

5.4.2 求解最大流问题

例5.4.1 求从城市v1到城市v6的最大流

5.4.3 最小费用最大流问题

例5.4.2（续例5.4.1）

5.5 Matlab图论工具箱

5.5.1 Matlab图论工具箱命令介绍

1、graphallshortestpaths 求图中所有顶点对之间的最短距离

2、graphshortestpath 求图中指定的一对顶点间的最短距离和最短路径

3、graphminspantree 在图中找最小生成树

4、graphmaxflow 计算有向图的最大流

5.5.2 应用举例

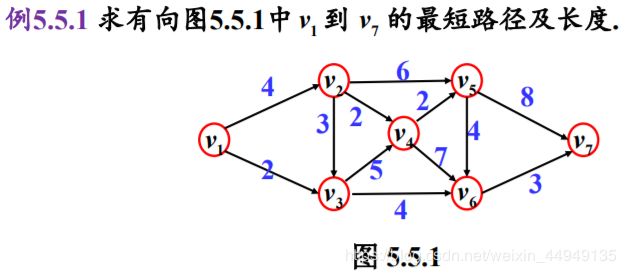
例5.5.1 求有向图5.5.1中v1到v7的最短路径及长度.

例5.5.2 求有向图5.5.2中从1到8的最大流.

5.6 渡河问题

1.问题描述

2.问题分析

3.模型建立

4.模型求解

5.结果分析

6.模型应用

5.7 钢管的订购与运输

1.问题描述

2.符号假设

3.模型的建立与求解

(一)运费矩阵的计算模型

(二)总费用的数学规划模型

(三)模型求解

4.结果分析

---

5.1 图的基本概念与数据结构

 图与网络模型：建模中常用来描述的离散型模型。比如：交通问题、通讯问题、优化问题。

5.1.1 图的基本概念

 

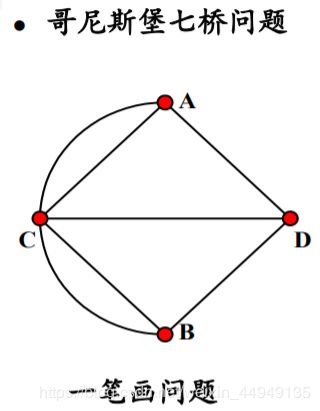
哥尼斯堡七桥问题               A B C D 四个城市 ------ 不重复、不遗漏地一次走完七座桥，最后回到出发点。

18世纪初普鲁士的哥尼斯堡，有一条河穿过，河上有两个小岛，有七座桥把两个岛与河岸联系起来。有个人提出一个问题：一个步行者怎样才能不重复、不遗漏地一次走完七座桥，最后回到出发点。后来大数学家欧拉把它转化成一个几何问题——一笔画问题。他不仅解决了此问题，且给出了连通图可以一笔画的充要条件是：奇点的数目不是0 个就是2 个（连到一点的数目如是奇数条，就称为奇点，如果是偶数条就称为偶点，要想一笔画成，必须中间点均是偶点，也就是有来路必有另一条去路，奇点只可能在两端，因此任何图能一笔画成，奇点要么没有要么在两端）。

七桥所成之图形中，没有一点含有偶数条数，因此上述的任务无法完成。

图论为任何一个包含了一种二元关系的离散系统提供了一个数学模型，借助于图论的概念、理论和方法，可以对该模型求解。哥尼斯堡七桥问题就是一个典型的例子。

1847年，德国物理学家克希霍夫为了给出电网络方程而引进了“树”的概念。哈密尔顿于1859年提出“周游世界”游戏，用图论的术语，就是如何找出一个连通图中的生成圈。近几十年来，由于计算机技术和科学的飞速发展，大大地促进了图论研究和应用，图论的理论和方法已经渗透到物理、化学、通讯科学、建筑学、运筹学、生物遗传学、心理学、经济学、社会学等学科中。

 边（弧，Edge）

节点：图中的点。         点集：节点的集合。         边集：边的集合。         e22：环         v1、v3：回路

---

• 既没有自环也没有平行边的图称为简单图(simple graph)。
• 在无向图中，与节点相关联边的数目，称为该节点的“度”(degree)， 记为 d ；度数为奇数的点称为奇点(odd)，度数为偶数的点称为偶点 (even) ；图中都是偶点的图称为偶图(even graph)。
• 可以 证明 任一图中 所有节点度数之和 为 边数的2倍。一条边，贡献两个度。

---

• 走过图中所有边且每条边仅走一次的闭和回路称为欧拉回路。
• 定理 5.1.1：偶图一定存在欧拉回路（一笔画定理）。
• 无向图中，若任意两点间至少存在一条路径，则称为连通图，否则为 非连通图。

---

 《数据结构》、《离散数学》

5.1.2 图与网络的数据结构

1.邻接矩阵表示法

 弧：第3行 第4列；行：起点；列：终点

 无向图，对称矩阵

2.稀疏矩阵表示法

在Matlab中无向图和有向图邻接矩阵的使用上有很大差异。

• 对于有向图，只要写出邻接矩阵，直接使用Matlab的命令sparse命令，就可以把邻接矩阵转化为稀疏矩阵的表示方式。
• 对于无向图，由于邻接矩阵是对称阵，Matlab中只需使用邻接矩阵的下三角元素，即Matlab只存储邻接矩阵下三角元素中的非零元素。
• 稀疏矩阵只是一种存储格式。Matlab中，普通矩阵使用sparse命令变成稀疏矩阵，稀疏矩阵使用full命令变成普通矩阵。

5.2 最短路问题

图论常见问题：最短路问题、最小生成树问题、最大流问题。

5.2.1 问题描述

最短路问题就是从给定的网络图中找出一点到各点或任意两点之间距离最短的一条路。

有些问题，如选址、管道铺设时的选线、设备更新、投资、某些整数规划和动态规划的问题，也可以归结为求最短路的问题。

因此这类问题在生产实际中得到广泛应用。

例5.2.1 求c1到其他城市的最短路

设计城市c1到其他城市间的票价最便宜路线图

5.2.2 两指定顶点间的最短路径模型

 规划模型 优化问题 图模型问题

：0-1变量         最短路：min：求所有边对应的权重         ：从i出发到j的标量

 ：求和（从顶点1出发的所有边 减去 到达顶点1的所有边）（i=1）

迪杰斯特拉算法：先找到到临近节点的最短距离，然后一步步向远处延伸。

（1）初始步

（2）循环步    顶点集V 去掉    

（3） i = |V| - 1   ：V的度-1

例5.2.1 求c1到其他城市的最短路

（1）求c1到其他城市的最短边。w16=10，最短。c1到c6，距离最短，将c6纳入S1中。将c6并入S1中。目标：S1、S1补集之间最短路        c1到c2、c3、c4、c5；c6到c1到c2、c3、c4、c5

（2）c1到c5、c6到c2，距离最短（权重最小）。将c1、c2、c5、c6并入S中。

（3）c5到c4，距离最短。找S2到S2补之间的最短路，保证不重复，避免重复搜索。

（4）c4到c3，距离最短。

• 1号城市：...
• 2号城市：c16 -> c62：c1到c6 -> c6到c2【10+25=35】
• 3号城市：c15 -> c54 -> c43【25+10+10=45】
• 4号城市：c15 -> c54【25+10=35】
• 5号城市：c15【25】
• 6号城市：c16【10】

5.2.3 每对顶点间的最短路径

计算赋权图中各对顶点之间的对短路径，显然可以调用Dijkstra算法，即每次以不同顶点作为起点，反复执行n-1次这样的操作, 但这种算法比较费时。另一种解决该问题的方法是由R.W.Floyd提出的，称为Floyd算法。

 每执行一步，寻求任意两顶点之间的最短路径。

例5.2.1 求c1到其他城市的最短路

if a(i, j) > a(i, k) +a(k, j)   a(i, j) = a(i, k) +a(k, j)：城市i到城市j，间接连线<直接连线，更新路径

a：任意两点之间的最短路径长度；path：经过的中间点

0 6 5 5 0 0：6表示---从c1到c2，中间要经过 点6。

% Floyd算法:
n=6; a=zeros(n); % 6*6的元素为0的初始矩阵
a(1,2)=50;a(1,4)=40;a(1,5)=25;a(1,6)=10; % 权值赋值
a(2,3)=15;a(2,4)=20;a(2,6)=25;           % 上三角矩阵
a(3,4)=10;a(3,5)=20;
a(4,5)=10;a(4,6)=25;
a(5,6)=55;
a=a+a'; % 转变为 对称邻接矩阵
a(a==0)=inf; % a中0元素，取值为∞
a([1:n+1:n^2])=0; % 主对角线元素为0
path=zeros(n); % 记录点

for k=1:n
    for i=1:n
        for j=1:n
            if a(i,j)>a(i,k)+a(k,j)
                % 间接路径代替直接路径
                a(i,j)=a(i,k)+a(k,j);
                path(i,j)=k; %经过k点找到最小路径
            end
        end
    end
end
a, path

有关Dijkstra算法和Floyd算法的Matlab实现 可以参考《数学建模算法与应用》第4.2节， 司守奎，孙玺菁著，国防工业出版社。

 【链接：https://pan.baidu.com/s/1q0RKTJ3gqPwCYBtqjBqn-g    提取码：zjxs】

5.3 最小生成树问题

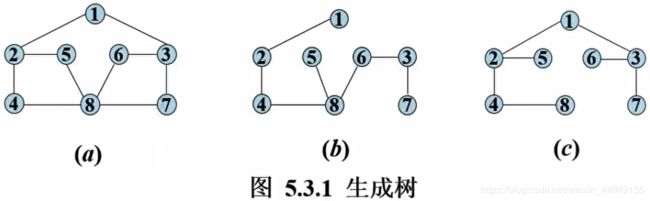
5.3.1 生成树

• 在包含n个顶点的无向连通图G中，经过所有顶点且包含n-1条边的连通子图G’称做 图G的生成树，一个图可以有多个生成树。生成树是连通图中的极小连通子图。
• 在图论中，常常将树定义为一个无回路连通图。

 b、c是a的连通子图、生成树。

5.3.2 最小生成树

对于一个带权的无向连通图，其每个生成树所有边上的权值之和可能不同，把所有边上权值之和最小的生成树称为图的最小生成树。

求图的最小生成树有很多实际应用。例如，通讯线路铺设造价最优问题就是一个最小生成树问题。假设把n个城市看作图的n个顶点，边表示两个城市之间的线路，每条边上的权值表示铺设该线路所需造价。铺设线路连接n个城市，但不形成回路，这就是图的生成树，而以最少的线路铺设造价连接各个城市，即求线路铺设造价最优问题，实际上就是在图的生成树中选择权值之和最小的生成树。

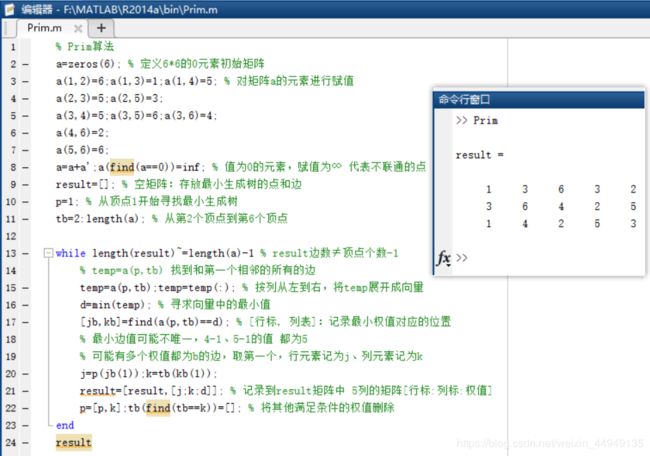
1.Prim算法

令集合P的初值为P={v1}：从图中给定的初始顶点v1出发，来寻找其最小生成树。集合Q的初值为空集（Ø），用来存放边。

v ∈ V - P，P={v1}：V减去v1后的剩余点。

从v1点开始，Q是空集。

while P不等于V（P中的点没有全部包含V中的点）

竖着看：1、3对应的权值为1；   3、6对应的权值为4...

% Prim算法
a=zeros(6); % 定义6*6的0元素初始矩阵
a(1,2)=6;a(1,3)=1;a(1,4)=5; % 对矩阵a的元素进行赋值
a(2,3)=5;a(2,5)=3;
a(3,4)=5;a(3,5)=6;a(3,6)=4;
a(4,6)=2;
a(5,6)=6;
a=a+a';a(find(a==0))=inf; % 值为0的元素，赋值为∞ 代表不联通的点
result=[]; % 空矩阵：存放最小生成树的点和边
p=1; % 从顶点1开始寻找最小生成树
tb=2:length(a); % 从第2个顶点到第6个顶点

while length(result)~=length(a)-1 % result边数≠顶点个数-1
    % temp=a(p,tb) 找到和第一个相邻的所有的边
    temp=a(p,tb);temp=temp(:); % 按列从左到右，将temp展开成向量
    d=min(temp); % 寻求向量中的最小值
    [jb,kb]=find(a(p,tb)==d); % [行标, 列表]：记录最小权值对应的位置
    % 最小边值可能不唯一，4-1、5-1的值 都为5
    % 可能有多个权值都为b的边，取第一个，行元素记为j、列元素记为k
    j=p(jb(1));k=tb(kb(1));
    result=[result,[j;k;d]]; % 记录到result矩阵中 5列的矩阵[行标:列标:权值]
    p=[p,k];tb(find(tb==k))=[]; % 将其他满足条件的权值删除
end
result

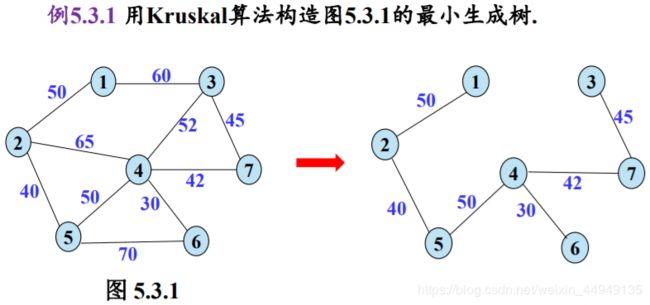
2. Kruskal算法

• Prim：从定点开始寻找...
• Kruskal：从最小权值的边，开始搜索...

按权值大小：4-6 --> 2-5 --> 4-7 --> 3-7 --> 1-2 --> 4-5      不能有回路，直到找到6条边。

5.4 网络最大流问题

网络最大流问题是网络的一个基本问题。许多系统包含了流量问题，例如交通系统有车流量，金融系统有现金流，控制系统有信息流等。许多流问题主要是确定这类系统网络所能承受的最大流量以及如何达到这个最大流量。

5.4.1 基本概念

1.网络与流

发点：从该点出发。    C={} ：以矩阵的形式 记录 对应弧的容量。

2.可行流与最大流

（1） ：0≤可行流≤容量限制（cij：弧上的容量）              （2）i≠s, t：不是发点、收点的中间点，流出量=流入量。

对于发点vs：：发点s流出的量    ：流入s点的量      实际流量v(f)：发点流出的量、收点流入的量

对于收点vt：考虑有向弧（流量有方向）     ：从t流出的量         ：流入t的量          -v(f)：实际流入t的量

在流量限制下，求最大流量（信息传输量、最大运输量）。

线性规划模型   目标函数：max v(f)---流量v(f)达到最大

• 发点：流出量v(f)
• 收点：流入量-v(f)
• 中间点：流出量-流入量=0

3.增广路

5.4.2 求解最大流问题

• 关于最大流问题的求解相关概念及方法，可参考《数学建模算法与应用》第4.3节。
• 《数学建模算法与应用》【链接：https://pan.baidu.com/s/1q0RKTJ3gqPwCYBtqjBqn-g    提取码：zjxs】
• 最大流算法的实现可以使用Matlab工具箱，可参考实验部分。

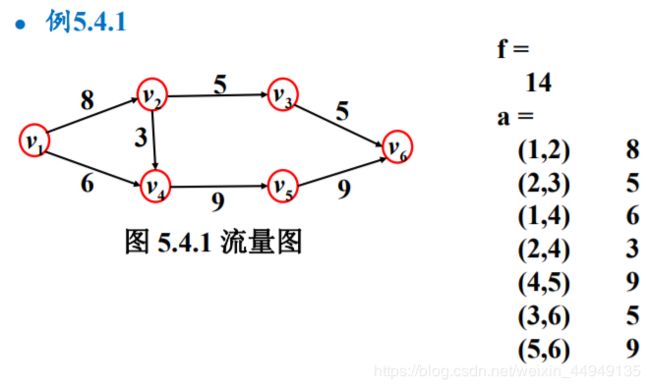
例5.4.1 求从城市v1到城市v6的最大流

 石油管道最大运输量

 f：最大流；a：最大流路径      流f(1, 2)为8...

% 求解最大流问题
n=6;c=zeros(n);
c(1,2)=8;c(1,4)=7;c(2,3)=9;c(2,4)=5;
c(3,4)=2;c(3,6)=5;c(4,5)=9;
c(5,3)=6;c(5,6)=10;
G=sparse(c); % 把邻接矩阵转化为稀疏矩阵 稀疏矩阵(G)形式存储矩阵c
[f, a]=graphmaxflow(G, 1, 6) % 求点1到点6的最大流

  

5.4.3 最小费用最大流问题

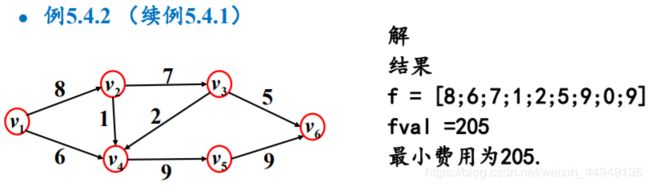
例5.4.2（续例5.4.1）

c=[8;7;9;5;2;5;9;6;10]; % 向量c：各个弧上的容量
b=[2 8 2 5 1 6 3 4 7];  % 对应的弧上的单位费用
a=zeros(6,9); % 6行9列的矩阵
a(1,1)=1;a(1,2)=1; % 弧为正方向,记为1;负方向,-1
a(2,1)=-1;a(2,3)=1;a(2,4)=1;
a(3,3)=-1;a(3,5)=1;a(3,6)=1;
a(4,2)=-1;a(4,4)=-1;a(4,5)=-1;
a(4,7)=1;
a(5,8)=1;a(5,7)=-1;a(5,9)=1;
a(6,6)=-1;a(6,9)=-1;
B=[14;0;0;0;0;-14]; % 14：出发点；-14：收点
lb=zeros(9,1);
ub=c; % 流的容量
[f,fval]=linprog(b,[],[],a,B,lb,ub) % 调用线性规划函数求解

5.5 Matlab图论工具箱

5.5.1 Matlab图论工具箱命令介绍

 帮助窗口

1、graphallshortestpaths 求图中所有顶点对之间的最短距离

• graphallshortestpaths调用格式

[dist] = graphallshortestpaths(G, ..., 'Directed', DirectedValue, ...)

[dist] = graphallshortestpaths(G, ..., 'Weights', WeightsValue, ...)

G是代表一个图的N*N稀疏矩阵，矩阵中的非零值代表一条边的权值；DirectedValue属性表示图是否为有向图，false代表无向图，true代表有向图，默认为true。WeightsValue是矩阵G中边的自定义权值列向量，该属性可以使我们使用零权值。输出[dist]是一个N*N的矩阵，每一个元素代表两点之间最短距离，对角线上的元素总为零，不在对角线上的零表示起点和终点的距离为零，inf值表示没有路径。

2、graphshortestpath 求图中指定的一对顶点间的最短距离和最短路径

• graphshortestpath调用格式

[dist, path] = graphshortestpath(G, S, T, 'Directed', Directedvalue)

G表示图的下三角稀疏矩阵；S是最短路的起点；T是最短路终点；Directed为有向图或无向图标志，Directedvalue是属性值，false（或 0）代表无向图，true（或1）代表有向图，默认为true。dist为得到的最短距离；path为得到的最短路径。

3、graphminspantree 在图中找最小生成树

• graphminspantree调用格式

[Tree, pred] = graphminspantree(G)

[Tree, pred] = graphminspantree(G, R)

[Tree, pred] = graphminspantree(..., 'Method' ,MethodValue, ...)

[Tree, pred] = graphminspantree(..., 'Weights', WeightsValue, ...)

该函数用来寻找一个无环的节点集合，连接无向图的全部节点，并且总的权值最小。Tree是一个代表生成树的稀疏矩阵，pred是包含 最小生成树的前驱节点的向量。G是无向图，R代表根节点，取值为1到节点数目，Method可以选择‘Kruskal’ , ’Prim’算法。

4、graphmaxflow 计算有向图的最大流

• graphmaxflow调用格式

[MaxFlow,FlowMatrix,Cut]=graphmaxflow(G,SNode,TNode)

[...] = graphmaxflow(G, SNode, TNode, ...'Capacity', CapacityValue, ...)

[...] = graphmaxflow(G, SNode, TNode, ...'Method', MethodValue, ...)

G是N*N的稀疏矩阵，表示有向图，SNode和TNode都是G中的节点，分别表示起点和终点，CapacityValue为每条边自定义容量的列向量；MethodValue 可以取 ‘ Edmonds ’ 和 ‘ Goldberg ’ 算 法。输 出 MaxFlow表示最大流，FlowMatrix是表示每条边数据流值的稀疏矩阵，Cut表示连接SNode到TNode的逻辑向量，如果有多个解时，Cut 是一个矩阵。若只有一个解，Cut表示逻辑向量。

5.5.2 应用举例

例5.5.1 求有向图5.5.1中v1到v7的最短路径及长度.

% 解 在matlab中构造该赋权有向图的邻接矩阵，并转化为稀疏矩阵.
a=zeros(7); % 7*7的稀疏矩阵
a(1,2)=4;a(1,3)=2;a(2,3)=3;a(2,4)=2;a(2,5)=6; % 将对应的有向向量及权值对a进行赋值
a(3,4)=5;a(3,6)=4;a(4,5)=2;a(4,6)=7;
a(5,6)=4;a(5,7)=8;a(6,7)=3;
b=sparse(a) %构造稀疏矩阵 将a存储为稀疏矩阵
[x,y]=graphshortestpath(b,1,7,'Directed',1) % 求最短路径及长度

例5.5.2 求有向图5.5.2中从1到8的最大流.

 网络最大流问题         3、4之间，存在回路

解：Matlab图论工具箱求解最大流的命令graphmaxflow，只能解决权重都为正值，且两个顶点之间不能有两条弧的问题，图5.5.2中顶点 3、4之间有两条弧，可在顶点4和顶点3之间加入一个虚拟的顶点9，并添加两条弧，删除顶点4到顶点3的权重为2的弧，加入的两条弧的容量都是2。

% 解：Matlab程序
a=zeros(9); % 加入虚拟顶点9   初始化9*9的矩阵
a(1,2)=6;a(1,3)=4;a(1,4)=5;a(2,3)=3;a(2,5)=9;a(2,6)=9; % 对 对应的弧 进行 容量赋值
a(3,4)=4;a(3,5)=6;a(3,6)=7;a(3,7)=3;
a(4,7)=5;a(4,9)=2;a(5,8)=12;a(6,5)=8;a(6,8)=10; % 删除弧a(4,3)=2，增加弧a(4,9)=2;
a(7,6)=4;a(7,8)=15;a(9,3)=2; % 增加弧a(9,3)=2; 9是虚拟添加的点，等价于a(4,3)=2
b=sparse(a) %构造稀疏矩阵 将a存储为稀疏矩阵
[x,y,z]=graphmaxflow(b,1,8)

 (1, 2)顶点的有向弧流量为6

z值：属性值向量，表示该网络流有唯一的最大流。

5.6 渡河问题

图模型应用：渡河问题。

1.问题描述

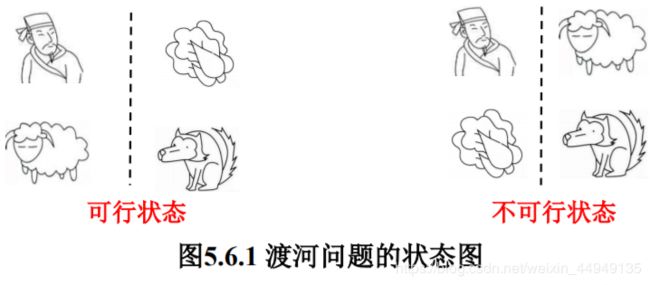
某人带狼、羊以及蔬菜渡河，一小船除需人划外，每次只能载一物过河。而人不在场时，狼要吃羊，羊要吃菜，问此人应如何过河？

2.问题分析

人或物的状态有两个：河此岸或河对岸。

在同一岸边，人不在场时，不能将狼和羊、羊和蔬菜放同一岸。

该问题可用图论中的最短路算法进行求解。

用四维向量表示人、狼、羊和菜的状态，在此岸时 状态取1，在对岸时 状态取0，例如，（1, 0, 1, 0）表示人和羊在此岸，狼和菜在对岸。

通过穷举法可列出所有可行的状态：

(1,1,1,1)，(1,1,1,0)，(1,1,0,1)，(1,0,1,1)，(1,0,1,0)，

(0,1,0,1)，(0,1,0,0)，(0,0,1,0)，(0,0,0,1)，(0,0,0,0).

每次渡河可改变现有状态为另一状态。

3.模型建立

构造赋权图G=(V，E，W)，顶点集合分别表示上述10个可行状态（按顺序编号）。当且仅当对应的两个可行状态之间存在一个可行转移时，两顶点之间才有边连接，并取对应权重为1，当两个顶点之间不存在可行转移时，可把对应权重取为∞。

问题变为在图G中寻找一条由初始状态（1,1,1,1）出发，经过最小次数转移到最终状态(0,0,0,0)的转移过程，即求从顶点到顶点的最短路径。

：人和物都在此岸；   ：人和物都在对岸。问题转化：求图中最短路径。

邻接矩阵

由于摆渡一次就改变现有状态，为此引入一个四维状态转移向量，用它来反映摆渡情况。用1表示渡河，用0表示未渡河。如 (1,1,0,0)表示人带狼渡河。状态转移只有4种情况，用如下向量表示：(1,0,0,0)，(1,1,0,0)，(1,0,1,0)，(1,0,0,1)

邻接矩阵

定义状态向量与转移向量之间的运算为：

0+0=0，1+0=1，0+1=1，1+1=0

第一个数字代表状态；第二个数字代表转移【对岸、未渡河->对岸；此岸、未渡河->此岸；对岸、渡河->此岸；此岸、渡河->对岸】

根据定义，如果某一可行状态加上转移向量得到的新向量还是可行状态，则这两个可行状态对应的顶点之间就存在一条边。用计算机编程时，可以利用普通向量的”异或”运算实现。             ^ 逻辑异或 a^b，a和b结果不同为true，相同为false

4.模型求解

用Matlab程序求解该最短路问题，如下

% clc,clear
% 10行4列向量 每行是一可行状态
a=[1 1 1 1;1 1 1 0;1 1 0 1;1 0 1 1;1 0 1 0; 0 1 0 1;0 1 0 0;0 0 1 0;0 0 0 1;0 0 0 0];
b=[1 0 0 0;1 1 0 0;1 0 1 0;1 0 0 1]; %每行是一转移状态
w=zeros(10); %邻接矩阵初始化
for i=1:9 %i表示第一个状态
    for j=i+1:10 %j表示另一个状态   上三角矩阵
        for k=1:4 % k表示渡河情况
            % 可行状态、转移状态之间的运算   a(j,:)：其它的可行状态
            if strfind(xor(a(i,:),b(k,:)),a(j,:)) %xor 表示异或运算
                w(i,j)=1; % 如果运算结果是其它的某一可行状态，令对应的w(i,j)=1,否则为0
            end
        end
    end
end
w=w'; %变成下三角矩阵
c=sparse(w); %构造稀疏矩阵
[x,y,z]=graphshortestpath(c,1,10,'Directed',0) %为无向图
h=view(biograph(c,[],'ShowArrows','off','ShowWeights','off')) %画无向图
Edges=getedgesbynodeid(h); %提取 h 中的边集

x = 7：需要渡河7次；      y：转移情况（1->6->3...）；      z：每个路径点的前驱节点

5.结果分析

图G的状态转移关系见图5.6.2，根据求解结果，可得完成过河需要渡河7次，顶点的状态转移顺序为1,6,3,7,2,8,5,10。

• 即第1次，人带羊到对岸；
• 第2次，人返回此岸；
• 第3次，人带菜到对岸；
• 第4次，人带羊到此岸；
• 第5次，人带狼到对岸；
• 第6次，人到此岸；
• 第7次，人带羊到对岸。

状态情况转移图      10个顶点，Node 1~Node 10，连接矩阵

6.模型应用

该问题的求解方法可以推广到类似背景，不同条件下问题的一般决策过程。例如，n个人，m个物在限定条件下调度问题，可通过调整状态向量和转移向量，类似求解方法来完成。

5.7 钢管的订购与运输

1.问题描述

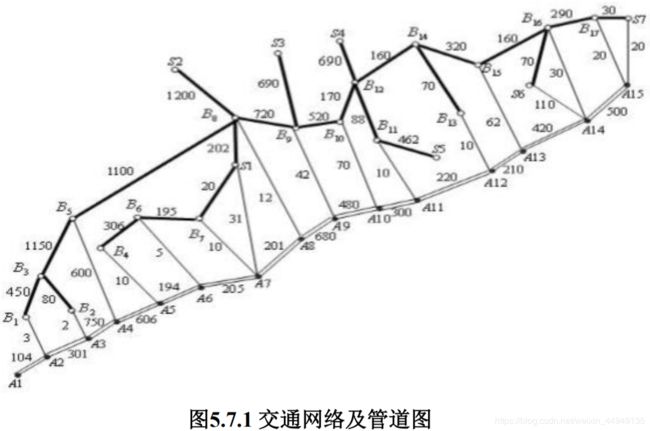
要铺设一条的输送天然气的主管道，如图5.7.1所示。经筛选后可以生产这种主管道钢管的钢厂有。图中粗线表示铁路，单细线表示公路，双细线表示要铺设的管道(假设沿管道或者原有公路，或者建有施工公路)，圆圈表示火车站，每段铁路、公路和管道旁的阿拉伯数字表示里程（单位：km）。

为方便计算，1km主管道钢管 称为 1单位钢管。

一家钢厂如果承担制造这种钢管，至少需要生产500个单位。钢厂在指定期限内能生产该钢管的最大数量为个单位，钢管出厂售价1单位钢管为万元，见表5.7.1；1单位钢管的铁路运价见表5.7.2。

1000km以上每增加1km~100km运价增加5万元。公路运输费为1单位钢管每千米0.1万元(不足整千米部分按整千米计算)。钢管可由铁路、公路运往铺设地点(不只是运到，而是管道全线)。

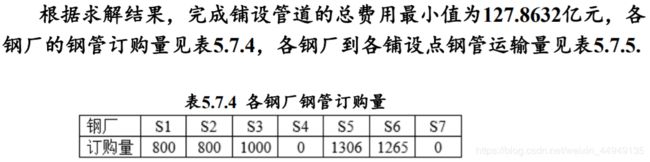
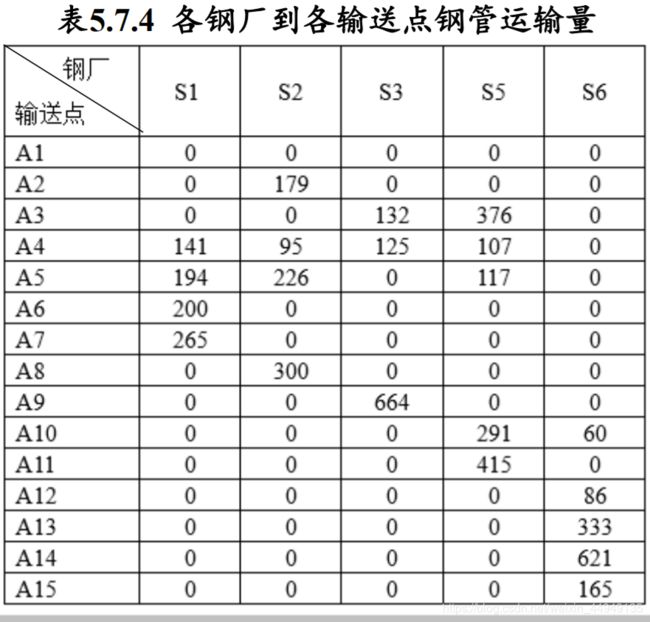
(1)请制定一个主管道钢管的订购与运输计划，使总费用最小(给 出总费用)。

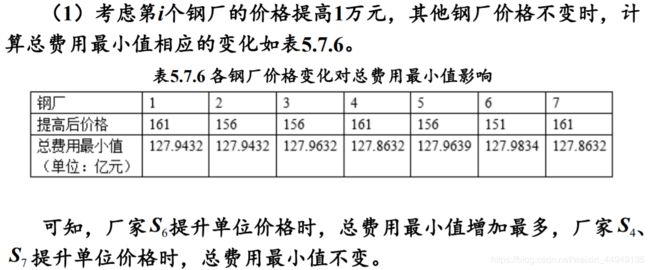
(2)请就(1)的模型分析：哪家钢厂钢管的销价的变化对购运计划和总费用影响最大，哪家钢厂的钢管的产量的上限的变化对购运计划和总费用的影响最大，并给出相应的数字结果。

2.符号假设

设

1. ：第i家钢厂的最大供应量   表5.7.1
2. ：从第i家钢厂到铺设节点j的订购和运输费用
3. ：管道第j段需要铺设的钢管量。   15个节点->14段管道
4. ：从钢厂i运到节点j的钢管量
5. ：从节点j向左铺设的钢管量
6. ：从节点j向右铺设的钢管量

3.模型的建立与求解

(一)运费矩阵的计算模型

根据问题所给的数据，可以先计算从供应点到需求点的最小购运费(即出厂售价和运输费用之和)，再根据求解总费用，总费用应包括：订购费用(包含在中)，运输费用(由各厂经铁路、公路运送至各点，i=1,2,...,7, j=1,2,…,15)，铺设管道的运费。

(一)运费矩阵的计算模型

(1)计算铁路任意两点间的最小运输费用

由于铁路运费不是连续的，故不能直接构造铁路费用赋权图，用Floyd算法来计算任意两点间的最小运输费用。但可以首先构造铁路距离赋权图，用Floyd算法计算任意两点间的最短铁路距离值，再依据表5.7.2中的铁路运价，求出任意两点间的最小铁路运输费用。

钢厂节点S1~S7，管道节点A1~A15，火车站位置B1~B17：一共39个节点   邻接矩阵W1

0.1：单位公路里程的运价

纵坐标：钢厂节点S1~S7；      横坐标：管道节点A1~A15          

(二)总费用的数学规划模型

xij对i求和：第i个钢厂到第j个节点的运输量。

xij：第i个钢厂到第j个节点的运输量。   下限 500；上限 si

(三)模型求解

model:
sets:
!nodes表示节点集合;
nodes/S1,S2,S3,S4,S5,S6,S7,A1,A2,A3,A4,A5,A6,A7,A8,A9,A10,A11,A12,A13,A14,A15,
B1,B2,B3,B4,B5,B6,B7,B8,B9,B10,B11,B12,B13,B14,B15,B16,B17/;
!c1(i,j)表示节点i到节点j铁路运输的最小运价(万元),c2(i,j)表示节点i到j公路运输的费用,
c(i,j)表示节点i到j的最小运价，path表示最短路径上走过的顶点;
link(nodes,nodes):w,c1,c2,c,path1,path;
supply/s1..s7/:S,P,f;
need/A1..A15/:b,y,z; !y表示每点往左铺设的量,z表示每点往右铺设的量;
linkf(supply,need):cf,x;
endsets
data:
S=800 800 1000 2000 2000 2000 3000;
P=160 155 155 160 155 150 161;
b=104,301,750,606,194,205,201,680,480,300,220,210,420,500,0;
path1=0;path=0;w=0;c2=0;
!以下是格式化输出计算的中间结果和最终结果;
@text(MiddleCost.txt)=@writefor(supply(i):@writefor(need(j):@format(cf(i,j),'6.1f')),@newline(1));
@text(Train_path.txt)=@writefor(nodes(i):@writefor(nodes(j):@format(path1(i,j),'5.0f')),@newline(1));
@text(Final_path.txt)=@writefor(nodes(i):@writefor(nodes(j):@format(path(i,j),'5.0f')),@newline(1));
@text(FinalResult.txt)=@writefor(supply(i):@writefor(need(j):@format(x(i,j),'5.0f')),@newline(1));
@text(FinalResult.txt)=@write(@newline(1));
@text(FinalResult.txt)=@writefor(need:@format(y,'5.0f'));
@text(FinalResult.txt)=@write(@newline(2));
@text(FinalResult.txt)=@writefor(need:@format(z,'5.0f'));
enddata
calc:
!输入铁路距离邻接矩阵的上三角元素;
w(1,29)=20;w(1,30)=202;w(2,30)=1200;w(3,31)=690;w(4,34)=690;w(5,33)=462;
w(6,38)=70;w(7,39)=30;w(23,25)=450;w(24,25)=80;w(25,27)=1150;w(26,28)=306;
w(27,30)=1100;w(28,29)=195;w(30,31)=720;w(31,32)=520;w(32,34)=170;w(33,34)=88;
w(34,36)=160;w(35,36)=70;w(36,37)=320;w(37,38)=160;w(38,39)=290;
@for(link(i,j):w(i,j)=w(i,j)+w(j,i));!输入铁路距离矩阵的下三角元素;
@for(link(i,j)|i#ne#j:w(i,j)=@if(w(i,j)#eq#0,20000,w(i,j)));!无铁路连接，元素为充分大的数;
!以下是最短路计算公式(Floyd-Warshall算法);
@for(nodes(k):@for(nodes(i):@for(nodes(j):tm=@smin(w(i,j),w(i,k)+w(k,j));
path1(i,j)=@if(w(i,j)#gt#tm,k,path1(i,j));w(i,j)=tm)));
!以下是按最短路w查找相应运费c1的计算公式;
@for(link|w#eq#0:c1=0);
@for(link|w#gt#0 #and# w#le#300:c1=20);
@for(link|w#gt#300 #and# w#le#350:c1=23);
@for(link|w#gt#350 #and# w#le#400:c1=26);
@for(link|w#gt#400 #and# w#le#450:c1=29);
@for(link|w#gt#450 #and# w#le#500:c1=32);
@for(link|w#gt#500 #and# w#le#600:c1=37);
@for(link|w#gt#600 #and# w#le#700:c1=44);
@for(link|w#gt#700 #and# w#le#800:c1=50);
@for(link|w#gt#800 #and# w#le#900:c1=55);
@for(link|w#gt#900 #and# w#le#1000:c1=60);
@for(link|w#gt#1000:c1=60+5*@floor(w/100-10)+@if(@mod(w,100)#eq#0,0,5));
!输入公路距离邻接矩阵的上三角元素;
c2(1,14)=31;c2(6,21)=110;c2(7,22)=20;c2(8,9)=104;
c2(9,10)=301;c2(9,23)=3;c2(10,11)=750;c2(10,24)=2;
c2(11,12)=606;c2(11,27)=600;c2(12,13)=194;c2(12,26)=10;
c2(13,14)=205;c2(13,28)=5;c2(14,15)=201;c2(14,29)=10;
c2(15,16)=680;c2(15,30)=12;c2(16,17)=480;c2(16,31)=42;
c2(17,18)=300;c2(17,32)=70;c2(18,19)=220;c2(18,33)=10;
c2(19,20)=210;c2(19,35)=10;c2(20,21)=420;c2(20,37)=62;
c2(21,22)=500;c2(21,38)=30;c2(22,39)=20;
@for(link(i,j):c2(i,j)=c2(i,j)+c2(j,i));!输入公路距离邻接矩阵的下三角元素;
@for(link(i,j):c2(i,j)=0.1*c2(i,j));!距离转化为费用;
@for(link(i,j)|i#ne#j:c2(i,j)=@if(c2(i,j)#eq#0,10000,c2(i,j)));!无公路连接，元素为充分大的数;
@for(link:c=@smin(c1,c2)); !c1和c2矩阵对应元素取最小;
@for(nodes(k):@for(nodes(i):@for(nodes(j):tm=@smin(c(i,j),c(i,k)+c(k,j));
path(i,j)=@if(c(i,j)#gt#tm,k,path(i,j));c(i,j)=tm)));
@for(link(i,j)|i#le#7 #and# j#ge#8 #and# j#le#22:cf(i,j-7)=c(i,j));!提取下面二次规划模型需要的7*15矩阵;
endcalc
[obj]min=@sum(linkf(i,j):(cf(i,j)+p(i))*x(i,j))+0.05*@sum(need(j):y(j)^2+y(j)+z(j)^2+z(j));
!约束;
@for(supply(i):[con1]@sum(need(j):x(i,j))<=S(i)*f(i));
@for(supply(i):[con2]@sum(need(j):x(i,j))>=500*f(i));
@for(need(j):[con3]@sum(supply(i):x(i,j))=y(j)+z(j));
@for(need(j)|j#ne#15:[con4]z(j)+y(j+1)=b(j));
y(1)=0;z(15)=0;
@for(supply:@bin(f));
@for(need:@gin(y));
end

4.结果分析