数学建模笔记 图论与网络优化
主要内容
- 前言
- Dijkstra算法
- Floyd算法
- Prim算法
- Kruskal算法
- 最小生成树的数学模型表示
- 最大流问题
前言
学图论算法的时候要被自己蠢哭了,第一次接触理解得很慢,所以花时间整理了一下,希望能加深一下印象。对于算法都是一些自己比较简单的理解,系统学习了数据结构后可能会有更深的思考。
Dijkstra算法
-
算法证明
归纳法证明:假设对于每次进入永久标号集合S的点ui,依照它的前驱形成的都是最短路。第一个入S的点为起点u1,它的前驱就是u1,显然u1到u1的最短路就是u1->u1,长度为0.假设第n个入队的点满足假设,那么对于第n+1个入队的点v来说,利用反证法,如果d[u1,v]不是u1到v的最短路径,存在另一条更短的路径,那么记该路径最后一个属于S的点为x,x经过若干个点最后到达v,记y是x的后继,那么d[u1,v]<=d[u1,y],(若d[u1,v]>d[u1,y],那么这次入S的便是y而不是v),所以d[u1,y]+d[y,v]>=d[u1,v],矛盾。 -
手动实现
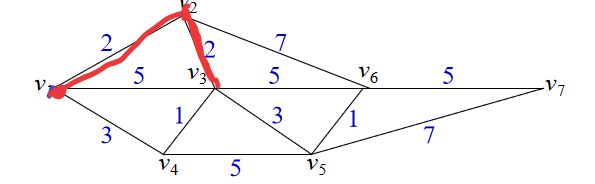
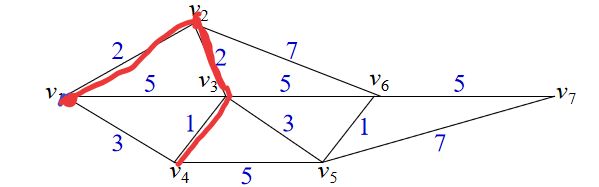
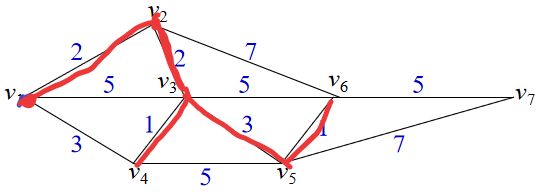
接下来手动实现一下以下图从1到8的最短路径
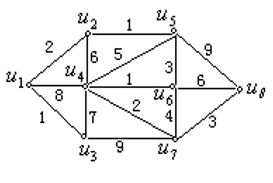
画方框的即为选中的前驱,右侧为相应点前驱的更新 
根据最终前驱得到最短路线:1->2->5->8
- 编程实现(matlab)
function pre=Dijkstra(A,s,e)
%A为邻接矩阵,s为起点,e为终点
num=size(A,1);
pre=zeros(1,num);%前驱集合
dist=zeros(1,num);%最短距离集合
V=[];%已选点集合
pre(1)=1;%初始化
dist(1)=0;
V(end+1)=1;
for i=2:num
dist(i)=inf;
end
PRE=1;%最新前驱
while 1
temp=zeros(1,num);
for j=1:num
temp(j)=inf;
end
for i=1:num
if (~checkin(V,i))
if dist(i)>dist(PRE)+A(i,PRE)
pre(i)=PRE;
dist(i)=dist(PRE)+A(i,PRE);
end
temp(i)=dist(i);
end
end
PRE=find(temp==min(temp));
V(end+1)=PRE;
if length(V)==num
break;
end
end
route=[e];
while(e~=s)
e=pre(e);
route(end+1)=e;
end
route%输出路线(反向看)
function flag=checkin(set,x)
flag=0;
for i=1:length(set)
if set(i)==x
flag=1;
end
end
clear;clc;
A=[0 2 1 8 inf inf inf inf;0 0 inf 6 1 inf inf inf;0 0 0 7 inf inf 9 inf;
0 0 0 0 5 1 2 inf;0 0 0 0 0 3 inf 9;0 0 0 0 0 0 4 6;0 0 0 0 0 0 0 3;0 0 0 0 0 0 0 0];
A=A+A';
pre=Dijkstra(A,1,8)
结果与手动结果一致
route =
8 5 2 1
pre =
1 1 1 6 2 5 4 5
- 理解
Dijkstra算法算是贪心思想实现的,首先把起点到所有点的距离存下来找个最短的,然后松弛一次再找出最短的,所谓的松弛操作就是,遍历一遍看通过刚刚找到的距离最短的点作为中转站会不会更近,如果更近了就更新距离,这样把所有的点找遍之后就存下了起点到其他所有点的最短距离。但缺点是只能计算由固定起点开始的最小路径,而以下介绍的floyd算法可以计算任意两点间的最短路径。
这个讲的蛮细致的:https://blog.csdn.net/lbperfect123/article/details/84281300
Floyd算法
-
算法证明
如果vi,vj间存在最短路径,(该路径中的子路径也是相应起点和终点的最短路径,)对于这条路径中任意相邻的三个点v1,v2,v3,当算法遍历到v2时,则会连接起来v1,v3,得到v1到v3的最短路径v1->v2->v3。当所有点遍历完成后,vi到vj的最短路径也就被找到了。 -
手动实现’
传送门:https://blog.csdn.net/SweeNeil/article/details/88713677
function route=Floyd(A,s,e)
num=size(A,1);
R=zeros(num,num);
for i=1:num
for j=1:num
R(i,j)=j;
end
end
D=A;
for k=1:num
for i=1:num
for j=1:num
if D(i,j)>D(i,k)+D(k,j)
D(i,j)=D(i,k)+D(k,j);
R(i,j)=k;
end
end
end
end
route=[e];
while 1
temp=e;
e=R(s,e);
if temp==e
break;
end
route(end+1)=e;
end
route(end+1)=s;
C=[0 2 5 3 inf inf inf;0 0 2 inf inf 7 inf;0 0 0 1 3 5 inf;0 0 0 0 5 inf inf;
0 0 0 0 0 1 7;0 0 0 0 0 0 5;0 0 0 0 0 0 0];
C=C+C';
route=Floyd(C,1,7)
结果:最短路径为:1->2->3->6->7
route =
7 6 5 3 2 1
当然用Dijkstra得出的结果是相同的:
route =
7 6 5 3 2 1
route =
1 1 2 1 3 5 6
Prim算法
-
算法描述
-
算法证明
欲证明每一次进入V1的边都属于最小生成树。第一次选择的是起点vi所在的最小权边e1,如果该边不在最小生成树内,那么将该边加入最小生成树,这时会形成一个圈,圈中含有e1和vi,此时去掉该圈中与vi相邻的另一条非e1边,显然该图仍为树,且权值和更小,这与原最小生成树矛盾,因此e1一定属于最小生成树。若前k条边都属于最小生成树(相关点记为u1,u2–uk-1),考虑第k+1条边,若第k+1条边ek+1不属于最小生成树,则将ek+1添加到最小生成树中会形成回路,该回路中含有前k条边所关联的若干点uj1…ujm,那么ujm一定会与u1-uk以外的点有边e,e的长度一定大于ek+1,那么将ek+1代替e仍是树,且权值和更小,矛盾。 -
编程实现
function mintree=Prim(A)
%一定要确保邻接矩阵对应的图是联通的,确保有最小生成树
num=size(A,1);
rand_start=1;
set=[];
set(end+1)=rand_start;
mintree=[];
while 1
temp1=[];
temp2=[];
temp3=[];
for i=set
if i~=0
for j=1:num
if ~checkin(set,j)
temp1(end+1)=A(i,j);
A(i,j)
else
temp1(end+1)=inf;
end
temp2(end+1)=i;
temp3(end+1)=j;
end
end
end
ind=find(temp1==min(temp1));
ind=ind(1);
set(end+1)=temp3(ind);
mintree(end+1,:)=[temp2(ind),temp3(ind)];
if length(set)==num
break;
end
end
C=[0 2 5 3 inf inf inf;0 0 2 inf inf 7 inf;0 0 0 1 3 5 inf;0 0 0 0 5 inf inf;
0 0 0 0 0 1 7;0 0 0 0 0 0 5;0 0 0 0 0 0 0];
C=C+C';
route=Prim(C);
结果
route =
1 2
2 3
3 4
3 5
5 6
6 7
Kruskal算法
-
算法证明
与Prim算法类似,欲证明每次新加进来的边都属于最小生成树。归纳法:利用与Prim相似的反证法易知e1属于最小生成树。将e1关联的两个点v1,v2缩为一个点,接下来再再找最小的点当然也在最小生成树中(若不在,则它与最小生成树形成回路,根据规则,不会与已经找到的边形成环,那么这个环中一定含有长度大于它的边,替换则得到新的最小生成树,矛盾),继续缩点查找直到找到n-1条边。那最后得到的这个图是树吗?根据查找规则,这个图一定是没有圈的,那么是否联通呢,假设联通分支数目m>=2 那么每个联通分支都是树,总边数为n-m -
算法实现
后续数据结构学习后会进行补充
最小生成树的数学模型表示

这里wij是权值,yij是表示点vi,vj是否相连(0,1),xij是通过vi,vj的流量(yij=0时,xij=0;yij>0时,xij表示vi->vj之后点的个数(包括vj))
总体目标就是权值和最小.
约束1:起点流量为n-1(n为总点数)
约束2:vj的入流量比出流量大1
约束3:其实就是:(yij=0时,xij=0;yij>0时,xij表示vi->vj之后点的个数(包括vj))
约束4:yij是表示点vi,vj是否相连(0,1)
最大流问题
- 问题描述
实际中很多应用系统都包含流量的问题,如公路系统中的车辆流,控制系统中的信息流、通信系统的呼叫流、供水系统中的水流、金融系统中的现金流等。对于这些系统,如何运行才能使系统获得最大流量? - 数学模型


例:
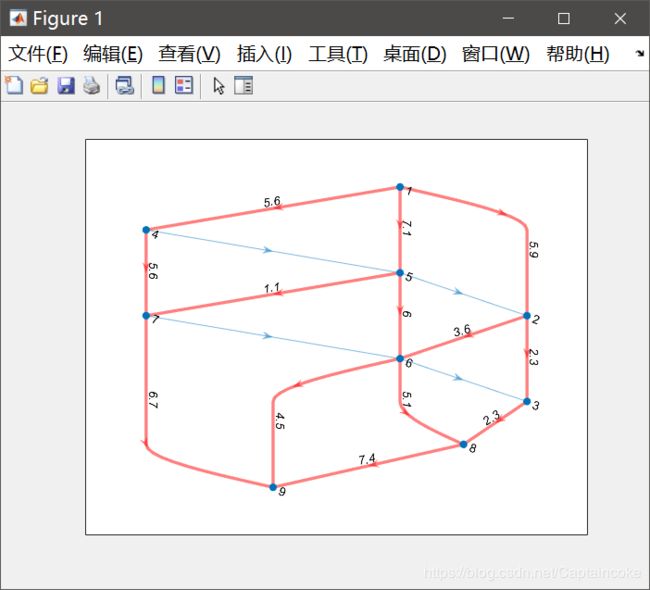
解决如下图的v1到v9的最大流问题:
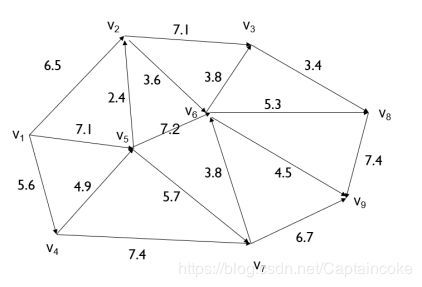
function [answer,fval]=maxflow2(A,s,e)
N=size(A,1);
m=N;
n=N*N+1;
M=zeros(m+2,n);
for k=1:m
if(k~=s & k~=e)
temp=ones(1,N);
temp(k)=0;
temp2=zeros(1,N*N);
temp2([k:N:N*N])=-1*ones(1,N);
temp2([N*(k-1)+1:1:N*(k-1)+N])=temp;
M(k,1:end-1)=temp2;
end
end
temp=ones(1,N);
temp(s)=0;
M(m+1,N*(s-1)+1:1:N*(s-1)+N)=temp;
M(m+1,end)=-1;
temp=zeros(1,N*N);
temp([e:N:N*N])=ones(1,N);
temp(e+(e-1)*N)=0;
M(m+2,:)=[temp -1];
coef=zeros(1,N*N+1);coef(end)=1;
up=[];
for i=1:N
up=[up A(i,:)];
end
up(end+1)=inf;
[answer fval]=linprog(-coef,[],[],M,zeros(size(M,1),1),zeros(n,1),up);
clear;clc;
A=zeros(9,9);
A(1,2)=6.5;A(1,5)=7.1;A(1,4)=5.6;A(5,2)=2.4;
A(4,5)=4.9;A(2,6)=3.6;A(5,6)=7.2;A(5,7)=5.7;A(4,7)=7.4;
A(7,6)=3.8;A(2,3)=7.1;A(6,3)=3.8;A(3,8)=3.4;A(6,8)=5.3;
A(8,9)=7.4;A(6,9)=4.5;A(7,9)=6.7;
s=1;e=9;
[arrangement,fval]=maxflow2(A,s,e);
N=size(A,1);
for i=1:9
for j=1:9
if(arrangement(N*(i-1)+j)>0)
fprintf("%d->%d:%.2f\n",i,j,arrangement(N*(i-1)+j));
end
end
end
S=[1 1 1 2 2 3 4 4 5 5 5 6 6 6 7 7 8];
E=[2 5 4 3 6 8 5 7 2 6 7 3 8 9 6 9 9];
weight=[6.5 7.1 5.6 7.1 3.6 3.4 4.9 7.4 2.4 7.2 5.7 3.8 5.3 4.5 3.8 6.7 7.4];
G=digraph(S,E,weight);
[x,GF]=maxflow(G,1,9);
H=plot(G,'EdgeLabel',G.Edges.Weight,'Layout','layered');
H.EdgeLabel = {};
highlight(H,GF,'EdgeColor','r','LineWidth',2);
st = GF.Edges.EndNodes;
labeledge(H,st(:,1),st(:,2),GF.Edges.Weight);
结果
1->2:5.90
1->4:5.60
1->5:7.10
2->3:3.40
2->6:2.50
3->8:3.40
4->7:5.60
5->6:6.00
5->7:1.10
6->8:4.00
6->9:4.50
7->9:6.70
8->9:7.40
maxflow=18.6
结果与matlab的图与网络包的结果一致,但各边的流量不尽相同,该最大流问题是多解的(暂时还不知道为啥,数据结构再往下学点应该就清晰了)
以下是matlab的流输出图: